BOJ 1760 - N-Rook 링크
(2023.06.26 기준 P3)

문제

N행 M열의 격자가 있다. 각 칸마다 상태가 주어지는데, 0은 빈 격자, 1은 구덩이가 파인 격자, 2는 벽이 놓인 격자이다.
이 격자에 룩을 놓으려고 하는데, 벽과 구덩이가 있는 격자엔 놓을 수 없고, 벽을 사이에 두고 있는 두 룩은 서로 공격할 수 없으나, 구덩이를 사이에 두고 있으면 두 룩은 서로 공격할 수 있다.
서로 공격할 수 없도록 최대한 배치 가능한 룩의 개수 출력

알고리즘

이분 매칭 응용 문제

풀이

룩은 벽에 가로막힐 때까지의 직선 상에 있는 모든 룩을 공격할 수 있다. 즉, 이어지는 직선 영역이 생긴다.

행 영역만 먼저 생각해보자.
벽이 없다고 가정했을 때에 같은 행에 룩 2개가 놓일 수 있을까? 불가능하다.
만약 행 가운데에 벽이 하나 있으면 벽을 사이에 두고 룩 2개가 놓일 수 있을까? 가능하다.
결국 벽으로 나눠지는 행 영역이 있을 때 각 영역마다 룩 하나씩만 들어올 수 있다.
열 영역도 마찬가지다.

자 이제 행과 열을 합쳐서 생각해보자.
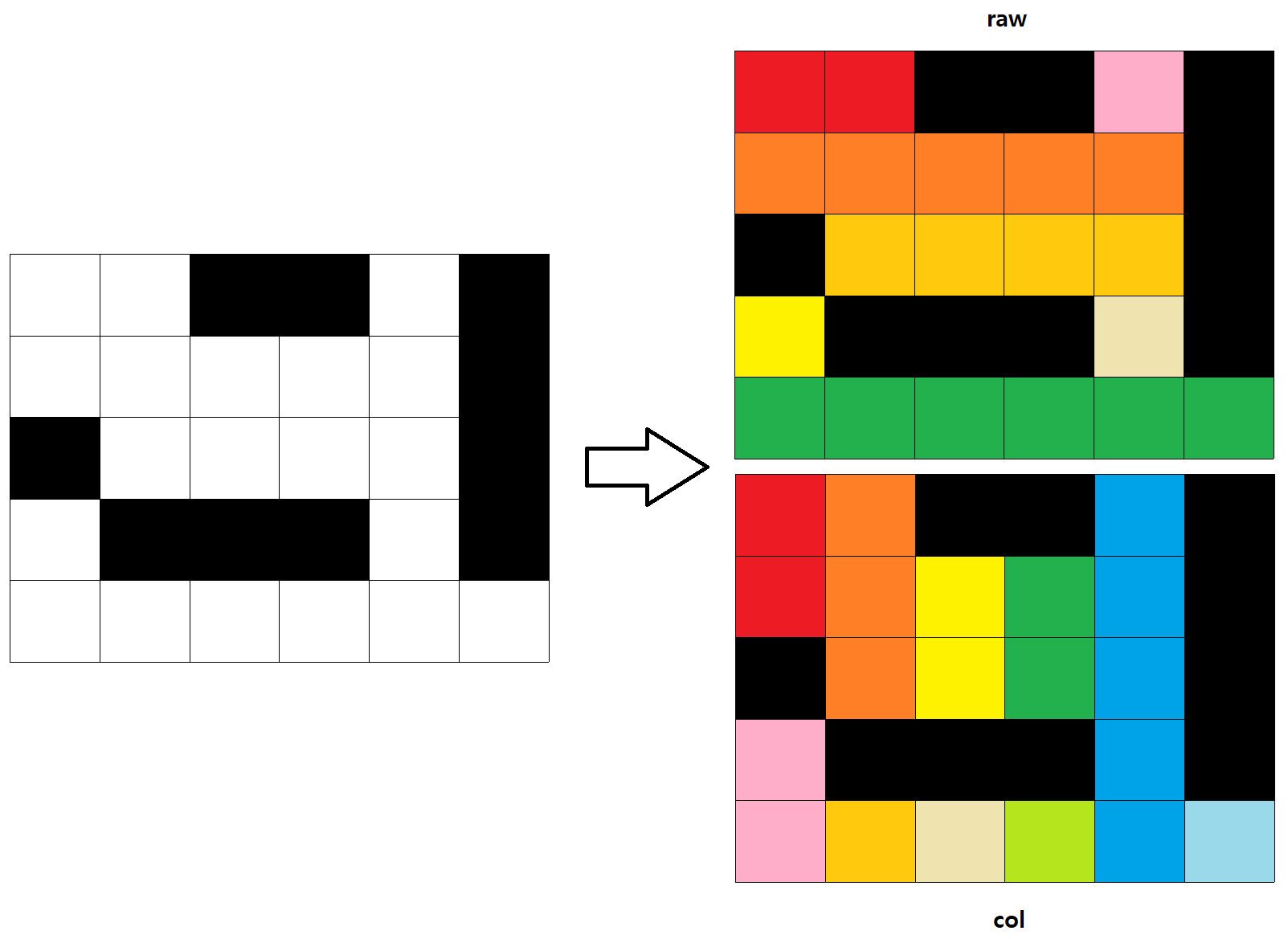
위 그림을 살펴보자. 검정은 벽이다.
각 칸은 행 영역 하나, 열 영역 하나에만 포함되어 있다. 그리고 어떤 칸에 룩을 놓게 되면 그 칸에 해당하는 행 영역과 열 영역에는 더 이상 룩을 놓지 못한다.
행 영역에는 여러 열 영역이 걸쳐져 있다. 반대로도 마찬가지. 그러므로, 각 칸마다 걸쳐져 있는 행과 열 영역 간 간선을 이은 그래프를 이용해 이분 매칭을 하면 된다.

한 영역에는 한 룩만 들어올 수 있으므로 칸, 행, 열이 아닌 영역을 한 정점으로 생각하면 된다.

영역은 다음과 같이 색칠하듯이 번호를 매기면 된다.

코드

• C++

#include <bits/stdc++.h>
using namespace std;

vector<vector<int>> graph;
vector<int> connect, visited;

// 이분 매칭
bool dfs(int i){
    for (int j: graph[i]){
        if (visited[j]) continue; // 이미 고려한 열이면 넘어가자.
        visited[j] = true;

        // 해당 열과 매칭된 행이 없거나 그 매칭된 행을 다시 매칭을 시도하여 성공할 경우
        if (connect[j] == -1 || dfs(connect[j])){
            connect[j] = i;
            return true;
        }
    }

    // 모두 실패하면 매칭 실패
    return false;
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    int N, M; cin >> N >> M;
    int matrix[N][M];
    for (int i = 0; i < N; i++) for (int j = 0; j < M; j++) cin >> matrix[i][j];

    // 행 영역 별로 번호를 매긴다.
    int raw[N][M], ri = 0;
    bool is_open = false; // 행이나 열이 이어지고 있는지 판별
    for (int i = 0; i < N; i++){
        for (int j = 0; j < M; j++){
            if (matrix[i][j] == 2){
                if (is_open) is_open = false, ri++;
            }
            else{
                if (!is_open) is_open = true;
                raw[i][j] = ri;
            }
        }
        if (is_open) is_open = false, ri++;
    }

    // 열 영역 별로 번호를 매긴다.
    int col[N][M], ci = 0;
    for (int j = 0; j < M; j++){
        for (int i = 0; i < N; i++){
            if (matrix[i][j] == 2){
                if (is_open) is_open = false, ci++;
            }
            else{
                if (!is_open) is_open = true;
                col[i][j] = ci;
            }
        }
        if (is_open) is_open = false, ci++;
    }

    // 각 격자마다 빈 격자라면 행 영역에서 열 영역으로 이어지는 간선을 그래프에 추가
    graph.resize(ri);
    for (int i = 0; i < N; i++) for (int j = 0; j < M; j++)
        if (!matrix[i][j]) graph[raw[i][j]].push_back(col[i][j]);

    // 각 행 영역 별로 이분 매칭 시도
    connect.resize(ci, -1);
    visited.resize(ci);
    int result = 0;
    for (int i = 0; i < ri; i++){
        fill(visited.begin(), visited.end(), false);
        if (dfs(i)) result++;
    }

    cout << result;
}

• Python

import sys; input = sys.stdin.readline

# 이분 매칭
def dfs(i):
    for j in graph[i]:
        if visited[j]: # 이미 고려한 열이면 넘어가자.
            continue
        visited[j] = True

        # 해당 열과 매칭된 행이 없거나 그 매칭된 행을 다시 매칭을 시도하여 성공할 경우
        if connect[j] == -1 or dfs(connect[j]):
            connect[j] = i
            return True

    # 모두 실패하면 매칭 실패
    return False

N, M = map(int, input().split())
matrix = [list(map(int, input().split())) for _ in range(N)]

# 행 영역 별로 번호를 매긴다.
raw = [[0] * M for _ in range(N)]; ri = 0
is_open = False # 행이나 열이 이어지고 있는지 판별
for i in range(N):
    for j in range(M):
        if matrix[i][j] == 2:
            if is_open:
                is_open = False
                ri += 1
        else:
            if not is_open:
                is_open = True
            raw[i][j] = ri
    if is_open:
        is_open = False
        ri += 1

# 열 영역 별로 번호를 매긴다.
col = [[0] * M for _ in range(N)]; ci = 0
for j in range(M):
    for i in range(N):
        if matrix[i][j] == 2:
            if is_open:
                is_open = False
                ci += 1
        else:
            if not is_open:
                is_open = True
            col[i][j] = ci
    if is_open:
        is_open = False
        ci += 1

# 각 격자마다 빈 격자라면 행 영역에서 열 영역으로 이어지는 간선을 그래프에 추가
graph = [[] for _ in range(ri)]
for i in range(N):
    for j in range(M):
        if not matrix[i][j]:
            graph[raw[i][j]].append(col[i][j])

# 각 행 영역 별로 이분 매칭 시도
connect = [-1] * ci
result = 0
for i in range(ri):
    visited = [False] * ci
    if dfs(i):
        result += 1

print(result)