BOJ 2261 - 가장 가까운 두 점 링크
(2023.04.11 기준 P2)
(치팅 절대 금지! 공부를 합시다!)

문제

2차원 평면상에 n개의 점이 주어질 때, 가장 가까운 두 점의 거리 출력

알고리즘

n이 최대 100,000 이라서 naive하게 푸는 O(nlgn)은 시간 초과가 난다. 분할 정복으로 풀어보자.

풀이

먼저 점들을 x 좌표 기준으로 정렬을 하자. 그리고 이분 탐색처럼 중간을 잡아 반으로 영역을 나눠보자.
각 영역의 점들의 최소 거리를 구했다고 치고, 두 거리 중 더 작은 값으로 현재 최소 거리라고 하자.

함수 dnc(l, r):
	mid = (l + r) / 2
    result = min(dnc(l, mid), dnc(mid + 1, r))

이제 두 영역을 합쳐야 한다.
합칠 때 영역의 맨 끝끼리 거리 계산? 절대 안된다.
이런 반례가 있다.
그러니 최소한의 점들로만 이루는 가운데 영역을 구해서 거리를 구해야 한다.
만약 mid인 점과의 x 좌표 차이가 아까 저장했던 '두 영역의 결과인 현재 최소 거리'보다 더 크다면? 어차피 가장 가까운 두 점의 후보가 되지 못한다.
이를 이용해 mid인 점의 x 좌표와의 차이가 현재 최소 거리보다 더 작은 점들만 가운데 영역에 저장하자. 같아도 안된다.

함수 dnc(l, r):
    ~
	# left
	for (int i = mid, i >= l, i--):
    	if (mid와 i의 x 좌표 차이 < result):
        	가운데 영역에 i 넣기
        else:
        	break
    # right
   	for (int i = mid + 1, i <= r, i++):
    	if (mid와 i의 x 좌표 차이 < result):
        	가운데 영역에 i 넣기
        else:
        	break

그리고 가운데 영역을 y 좌표 기준으로 정렬해주자.
이제 가운데 영역에서의 점들끼리 거리를 구할건데, 위에서 x 좌표 차이로 가지치기한 것처럼 이번엔 y 좌표 차이로 가지치기를 하면 된다.

함수 dnc(l, r):
    ~
	가운데 영역 y 기준으로 정렬
    for (int i = 0, i < 가운데 영역 크기 - 1, i++):
    	for (int j = i + 1, j < 가운데 영역 크기, j++):
        	if (i와 j의 y 좌표 차이 < result):
           		result = min(result, i와 j의 거리)
            else:
            	break

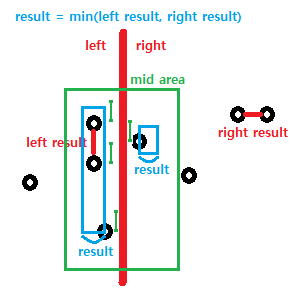
그림으로 나타내면 이렇다.

빨강 -> 파랑 -> 초록 순으로 보면 이해가 갈 것이다.
1. 빨강 : 왼쪽, 오른쪽 영역에서 각 최소 거리를 찾는다.
2. 파랑 : x 좌표 기준으로 mid인 점과의 거리가 찾은 최소 거리보다 더 멀면 고려하지 않는다.
3. 초록 : 파랑에서 찾은 점들로 이루어진 영역 중에서 하나씩 거리를 찾아보되, y 좌표 기준으로 기준인 점과의 거리가 찾은 최소 거리보다 더 멀면 고려하지 않는다.

빨강이 좀 의아할 수 있다. 하지만 이는 분할 정복.
끝까지 분할하다 보면 점이 하나가 나온다. 점 하나는 거리가 없으므로 무한대를 반환하자. 그리고 한 점이 있는 영역 2개가 합쳐지면 그 한 점끼리의 거리가 반환이 될 것이다. 이런게 바로 분할 정복이다..!

코드

• C++

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pll;
const ll inf = 1e16;

vector<pll> points;

bool cmp(pll a, pll b){ // y 기준 정렬
    return a.second < b.second;
}

ll distance(pll a, pll b){
    return (a.first - b.first) * (a.first - b.first) + (a.second - b.second) * (a.second - b.second);
}

ll dnc(int st, int en){
    if (st == en) return inf; // 하한과 상한이 같으면 점이 하나이므로 무한대 반환

    int mid = (st + en) >> 1;
    ll result = min(dnc(st, mid), dnc(mid + 1, en)); // 두 분할 정복의 결과 중 작은 값이 현재 최소 거리

    // mid인 점과의 x 좌표 차이가 현재 최소 거리보다 작은 점들만 가운데 영역에 저장
    vector<pll> mid_points;
    for (int i = mid; i >= st; i--){
        if ((points[mid].first - points[i].first) * (points[mid].first - points[i].first) < result) mid_points.push_back(points[i]);
        else break;
    }
    for (int i = mid + 1; i <= en; i++){
        if ((points[i].first - points[mid + 1].first) * (points[i].first - points[mid + 1].first) < result) mid_points.push_back(points[i]);
        else break;
    }

    // y를 기준으로 정렬 후 y 좌표 차이가 현재 최소 거리보다 작은 동안만 검사 및 답 갱신
    sort(mid_points.begin(), mid_points.end(), cmp);
    for (int i = 0; i + 1 < mid_points.size(); i++) for (int j = i + 1; j < mid_points.size(); j++){
        if ((mid_points[j].second - mid_points[i].second) * (mid_points[j].second - mid_points[i].second) < result) result = min(result, distance(mid_points[i], mid_points[j]));
        else break;
    }
    return result;
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    int n;
    cin >> n;

    int x, y;
    for (int i = 0; i < n; i++){
        cin >> x >> y;
        points.push_back({x, y});
    }
    sort(points.begin(), points.end()); // x를 기준으로 정렬

    cout << dnc(0, n - 1);
}

• Python

import sys; input = sys.stdin.readline
from math import inf

def distance(a, b): # 거리
    return (a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2

def dnc(start, end):
    if start == end: # 하한과 상한이 같으면 점이 하나이므로 무한대 반환
        return inf

    mid = (start + end) // 2
    result = min(dnc(start, mid), dnc(mid + 1, end)) # 두 분할 정복의 결과 중 작은 값이 현재 최소 거리

    # mid인 점과의 x 좌표 차이가 현재 최소 거리보다 작은 점들만 가운데 영역에 저장
    mid_points = []
    for i in range(mid, start - 1, -1):
        if (points[mid][0] - points[i][0]) ** 2 < result:
            mid_points.append(points[i])
        else:
            break
    for i in range(mid + 1, end + 1):
        if (points[i][0] - points[mid + 1][0]) ** 2 < result:
            mid_points.append(points[i])
        else:
            break

    # y를 기준으로 정렬 후 y 좌표 차이가 현재 최소 거리보다 작은 동안만 검사 및 답 갱신
    mid_points.sort(key = lambda x: x[1])
    for i in range(len(mid_points) - 1):
        for j in range(i + 1, len(mid_points)):
            if (mid_points[j][1] - mid_points[i][1]) ** 2 < result:
                result = min(result, distance(mid_points[i], mid_points[j]))
            else:
                break
    return result

n = int(input())
points = sorted(list(map(int, input().split())) for _ in range(n)) # x를 기준으로 정렬

print(dnc(0, n - 1))