BOJ 2275 - 트리의 높이 줄이기 링크
(2024.03.22 기준 G1)

문제

$N$개의 정점을 갖는 루트 있는 트리가 있고, 이 트리의 높이는 루트에서 가장 멀리 떨어져 있는 정점까지의 거리를 의미한다.

간선의 가중치를 $1$씩 줄일 때마다 $1$만큼의 비용이 든다. 이때, 주어지는 트리의 높이를 $H$로 만들기 위한 최소 비용 출력

알고리즘

그리디

풀이

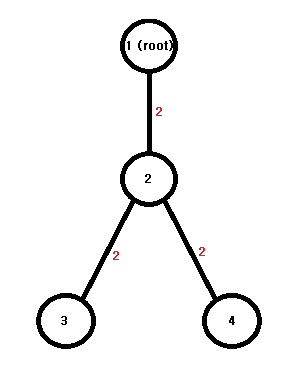
위와 같은 트리의 높이를 $3$으로 줄인다고 생각을 해보자.
$(1,2)$ 간선의 가중치를 $1$로 줄이면 총 비용은 $1$이다.
$(2,3)$, $(2,4)$ 두 간선의 가중치를 $1$로 줄이면 총 비용은 $2$이다.

트리에서의 각 정점은 부모는 하나, 자식은 하나 이상이다. 즉, 트리 전체의 가중치를 줄이기 위해선, 루트와 먼 곳의 가중치를 여럿 줄이는 것보다 루트와 가까운 곳의 가중치를 줄이는 것이 당연히 이득임을 알 수 있다.

$dist1(i)$는 루트에서 $i$번 정점까지의 거리, $dist2(i)$는 $i$번 정점을 루트로 하는 서브트리의 최대 높이를 뜻하게끔 두 배열을 만들어보자.

이제 $f(i, cost)$를 현재 $cost$만큼 비용이 들었고 $i$번 정점을 보고 있을 때, $i$번 정점을 루트로 하는 서브트리의 최소 비용을 반환하는 함수라고 하자.

$i$번 정점에서 자식들을 향해 나아가는 간선 $(i,j,k)$를 살펴보자. 이때, $j$는 자식 정점의 번호이고 $k$는 간선의 가중치이다.

현재 $j$번 정점을 지나는 트리의 높이 $height_j$는 $dist1(j) + dist2(j) - cost$가 된다. $height_j$가 $H$보다 같거나 작다면 그냥 넘어간다. 이미 조건을 만족하기 때문이다.

하지만 $height_j$가 $H$보다 크다면? 현재 간선의 가중치를 줄여야 한다. 그 값은 $min(k, dist1[j] + dist2[j] - cost - H)$가 된다. 일단 현재 간선의 가중치보다 더 많이 줄일 수 없다. 그리고 현재 높이가 H를 초과하는 만큼보다 더 줄이면 최소 비용이 되지 않는다.
이렇게 구한 줄이는 값을 $c$, $f(i, cost)$가 반환하는 값 $res$라고 했을 때, $res = res + f(j, cost + c) + c$가 된다.

코드

• C++

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> pii;

const int MAXN = 10001;

int N, H, dist1[MAXN], dist2[MAXN];
vector<pii> G[MAXN];

int dfs1(int i){
    for (auto [j, k]: G[i]){
        dist1[j] = dist1[i] + k;
        dist2[i] = max(dist2[i], dfs1(j) + k); // 최대 높이
    }
    return dist2[i];
}

int dfs2(int i, int cost){ // 현재 정점, 현재 비용 (줄인 횟수)
    int res = 0;
    for (auto [j, k]: G[i]){
        if (dist1[j] + dist2[j] - cost <= H) continue; // j번을 지나는 높이가 이미 H 이하라면 패스
        int c = min(k, dist1[j] + dist2[j] - cost - H); // 최대 간선의 가중치만큼 줄일 수 있다.
        res += dfs2(j, cost + c) + c;
    }
    return res;
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    cin >> N >> H;

    int root;
    for (int i = 1, j, k; i <= N; i++){
        cin >> j >> k;
        if (j) G[j].push_back({i, k});
        else root = i;
    }

    // 부모 쪽에서 간선의 가중치를 줄이면 자식들의 높이도 같이 줄어든다.
    // 즉, 루트와 가까운 쪽에서 가능한 많이 줄여야 이득이다.

    fill(dist1 + 1, dist1 + N + 1, 0); // dist1(i) : 루트에서 i번 정점까지의 거리
    fill(dist2 + 1, dist2 + N + 1, 0); // dist2(i) : i번 정점을 루트로 하는 서브트리의 최대 높이
    dfs1(root);

    cout << dfs2(root, 0);
}

• Python

import sys; input = sys.stdin.readline
sys.setrecursionlimit(11111)

def dfs1(i):
    for j, k in G[i]:
        dist1[j] = dist1[i] + k
        dist2[i] = max(dist2[i], dfs1(j) + k) # 최대 높이
    return dist2[i]

def dfs2(i, cost): # 현재 정점, 현재 비용 (줄인 횟수)
    res = 0
    for j, k in G[i]:
        if dist1[j] + dist2[j] - cost <= H: # j번을 지나는 높이가 이미 H 이하라면 패스
            continue
        c = min(k, dist1[j] + dist2[j] - cost - H) # 최대 간선의 가중치만큼 줄일 수 있다.
        res += dfs2(j, cost + c) + c
    return res

N, H = map(int, input().split())

G = [[] for _ in range(N + 1)]
for i in range(1, N + 1):
    j, k = map(int, input().split())
    if j:
        G[j].append((i, k))
    else:
        root = i

# 부모 쪽에서 간선의 가중치를 줄이면 자식들의 높이도 같이 줄어든다.
# 즉, 루트와 가까운 쪽에서 가능한 많이 줄여야 이득이다.

dist1 = [0] * (N + 1) # dist1(i) : 루트에서 i번 정점까지의 거리
dist2 = [0] * (N + 1) # dist2(i) : i번 정점을 루트로 하는 서브트리의 최대 높이
dfs1(root)

print(dfs2(root, 0))