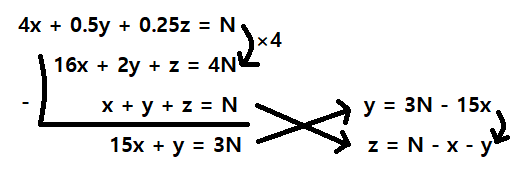BOJ 4486 - Pencils from the 19th Century 링크
(2023.04.13 기준 B2)

문제

한 개당 4센트, 두 개당 1센트, 네 개당 1센트인 연필들이 있다고 하자.
N센트로 N개의 연필을 샀을 때, 가능한 연필들의 경우의 수 출력

알고리즘

간단한 방정식 및 방정식의 해를 브루트포스로 찾기

풀이

두 개당 1센트는 곧, 한 개당 0.5센트. 네 새당 1센트는 곧, 한 개당 0.25센트이다.
문제에서 주어진 방정식은 두 개다.
4x + 0.5y + 0.25z = N
x + y + z = N

이 방정식을 대충 한번 풀어보면 다음과 같다.

연필의 개수는 0이나 음수가 될 수 없다. 그러므로 가능한 x의 범위는? [1, N - 2] 이다.
그러므로 이 범위 안에서 x를 정해주면서 풀면? 남은 미지수는 2개, 방정식도 2개이므로 풀린다.
그러므로 y, z도 구해준 다음에, 각 y, z가 자연수인지 확인하면 된다.

코드

• C++

#include <bits/stdc++.h>
using namespace std;
typedef tuple<int, int, int> tiii;

int N, x, y, z;

// 16x + 2y + z = 4N
// x + y + z = N
// y = 3N - 15x
// z = N - x - y
// 모든 종류의 연필을 1개 이상 가져야 하므로
// x > 0 && y > 0 && z > 0
void solve(){
    vector<tiii> result;
    for (x = 1; x <= N - 2; x++){ // x의 범위는 [1, N - 2]
        y = N * 3 - x * 15;
        z = N - x - y;
        if (y > 0 && z > 0) result.push_back({x, y, z});
    }

    if (result.empty()){
        cout << "No solution found.\n\n";
        return;
    }

    for (auto xyz: result){
        cout << get<0>(xyz) << " at four cents each\n";
        cout << get<1>(xyz) << " at two for a penny\n";
        cout << get<2>(xyz) << " at four for a penny\n\n";
    }
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    int T = 0;
    for (cin >> N; N; cin >> N){
        cout << "Case " << ++T << ":\n";
        cout << N << " pencils for " << N << " cents\n";
        solve();
    }
}

• Python

import sys; input = sys.stdin.readline

T = 0
while True:
    N = int(input())
    if not N:
        break
    T += 1
    print('Case %d:' % T)
    print('%d pencils for %d cents' % (N, N))

    # 16x + 2y + z = 4N
    # x + y + z = N
    # y = 3N - 15x
    # z = N - x - y
    # 모든 종류의 연필을 1개 이상 가져야 하므로
    # x > 0 and y > 0 and z > 0
    result = []
    for x in range(1, N - 1): # x의 범위는 [1, N - 2]
        y = N * 3 - x * 15
        z = N - x - y
        if y > 0 and z > 0:
            result.append([x, y, z])

    if not result:
        print('No solution found.\n')
        continue

    for x, y, z in result:
        print('%d at four cents each' % x)
        print('%d at two for a penny' % y)
        print('%d at four for a penny\n' % z)