BOJ 5419 - 북서풍 링크
(2023.08.02 기준 P4)

문제

섬이 n개가 있는 바다가 있다. 각 섬에서는 동쪽과 남쪽 사이의 모든 방향으로만 항해할 수 있다. 항해할 수 있는 섬의 쌍의 수 출력

알고리즘

좌표 압축된 섬의 위치에 따른 개수를 세그먼트 트리에 담고 스위핑

풀이

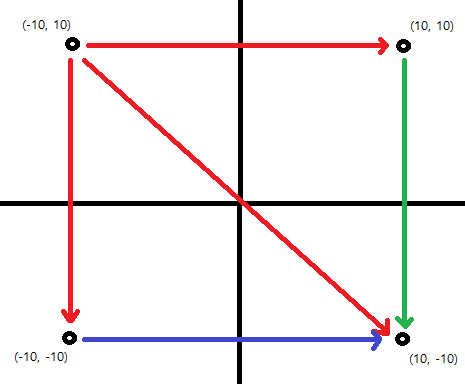
문제를 요약하자면, 한 섬에서 동쪽과 남쪽 사이의 모든 방향에 있는 모든 섬들의 개수를 모든 섬마다 구하는 것이다.

첫번째 예시를 보자.

한 섬에서 짝지을 수 있는 섬들은 결국 x 좌표는 같거나 커야 하고, y 좌표는 같거나 작아야 한다.

일단, 먼저 좌표의 범위가 [-10e9, 10e9]이기 때문에, 좌표 압축을 해준다. 그리고 x 좌표가 같은 섬끼리 전부 모아두고, 모아둔 섬끼리는 y 좌표가 내림차순이 되게 모으자. 모으면서 펜윅트리와 같은 구조에 각 섬의 y 좌표의 위치에 섬이 하나 있다는 표식 느낌으로 1씩 증가시켜주자.

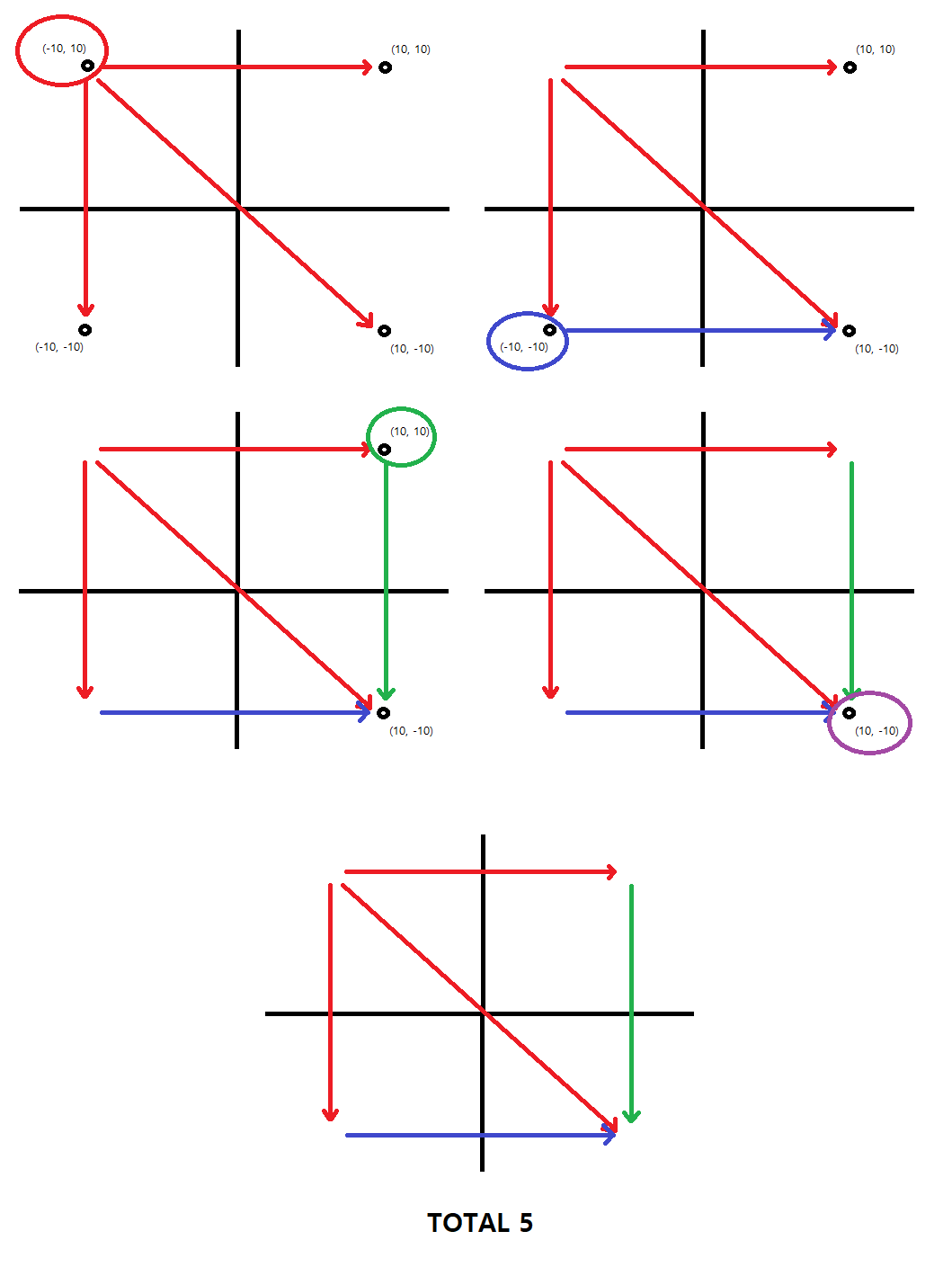
그리고 x 좌표가 오름차순, y 좌표는 내림차순이 되게끔 훑으면서 1~y에 있는 섬의 개수를 구간합 쿼리로 구해가면서 스위핑하면 된다.

첫번째 예시를 들면 다음과 같이 진행되는 것이다.

주의사항

C++에서 섬의 쌍의 수를 구할 때 int 범위를 초과할 수 있는 답이 나올 수 있다.
만약 동쪽이나 남쪽으로 섬이 일직선으로 나열되어 있고 섬의 개수가 75,000개이면
총 섬의 쌍의 수는 75,000 × 74,999 ÷ 2 = 2,812,462,500 가 나온다.

코드

• C++

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;

const int MAXN = 75000;

int n;
vector<int> X, Y;
vector<pii> points;

struct FW{ // fenwick
    int tree[MAXN + 1];
    vector<int> points[MAXN];

    void init();

    void _update(int nd, int val){
        while (nd <= n){
            tree[nd] += val;
            nd += nd & -nd;
        }
    }

    int _query(int nd){
        int result = 0;
        while (nd > 0){
            result += tree[nd];
            nd -= nd & -nd;
        }
        return result;
    }

    void run(){
        for (int i = 0; i < n; i++){
            sort(points[i].begin(), points[i].end(), greater<>()); // y 좌표는 내림차순으로 정렬
            for (int j: points[i]) _update(j, 1); // y에 대한 위치에 1 증가
        }

        // x 오름차순 y 내림차순으로 스위핑
        ll result = 0;
        for (int i = 0; i < n; i++) for (int j: points[i]){
            _update(j, -1); // 현재 섬은 이제 더 이상 카운트되지 못하므로 1 감소
            result += _query(j); // y 좌표가 1~j 섬인 섬들과 쌍을 지을 수 있다.
        }
        cout << result << '\n';
    }
}fw;

void FW::init(){
    fill(tree + 1, tree + n + 1, 0);
    for (int i = 0; i < n; i++) points[i].clear();
}

void compress(vector<int> &A){ // 좌표 압축
    sort(A.begin(), A.end());
    A.erase(unique(A.begin(), A.end()), A.end());
}

void solve(){
    cin >> n;
    fw.init();

    // 좌표 압축 후 x 좌표가 같은 섬끼리 모은다.
    // 펜윅을 위해 y 좌표의 압축 후는 1-based index
    points.clear(); X.clear(); Y.clear();
    for (int i = 0, x, y; i < n; i++){
        cin >> x >> y;
        points.push_back({x, y});
        X.push_back(x); Y.push_back(y);
    }
    compress(X); compress(Y);
    for (auto [x, y]: points)
        fw.points[lower_bound(X.begin(), X.end(), x) - X.begin()].push_back(lower_bound(Y.begin(), Y.end(), y) - Y.begin() + 1);

    fw.run();
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    int T; cin >> T;
    while (T--) solve();
}

• Python

import sys; input = sys.stdin.readline
from bisect import bisect_left

class FW: # fenwick
    def __init__(self, n):
        self.n = n
        self.tree = [0] * (self.n + 1)
        self.points = [[] for _ in range(self.n)]

    def _update(self, nd, val):
        while nd <= self.n:
            self.tree[nd] += val
            nd += nd & -nd

    def _query(self, nd):
        result = 0
        while nd > 0:
            result += self.tree[nd]
            nd -= nd & -nd
        return result

    def run(self):
        for i in range(self.n):
            self.points[i].sort(reverse = True) # y 좌표는 내림차순으로 정렬
            for j in self.points[i]:
                self._update(j, 1) # y에 대한 위치에 1 증가

        # x 오름차순 y 내림차순으로 스위핑
        result = 0
        for i in range(self.n):
            for j in self.points[i]:
                self._update(j, -1) # 현재 섬은 이제 더 이상 카운트되지 못하므로 1 감소
                result += self._query(j) # y 좌표가 1~j 섬인 섬들과 쌍을 지을 수 있다.
        print(result)

def solve():
    n = int(input())
    fw = FW(n)

    # 좌표 압축 후 x 좌표가 같은 섬끼리 모은다.
    # 펜윅을 위해 y 좌표의 압축 후는 1-based index
    points = [tuple(map(int, input().split())) for _ in range(n)]
    X, Y = map(lambda x: sorted(set(x)), zip(*points))
    for x, y in points:
        fw.points[bisect_left(X, x)].append(bisect_left(Y, y) + 1)

    fw.run()

for _ in range(int(input())):
    solve()