수요일은 산뜻하게 scc로 시작하자.

BOJ 6543 - 그래프의 싱크 링크
(2022.10.05 기준 P4)
(치팅은 나빠요)

문제

어떤 노드가 자신으로부터 도달할 수 있는 모든 노드로부터 돌아오는 경로가 있다면 그 노드는 싱크라고 한다면, 그래프 G의 모든 싱크를 출력

알고리즘

방향 그래프에서 SCC를 만들어 묶어서 다시 그래프로 표현하면 DAG가 된다. 이 DAG에서 도달 가능한 모든 노드로부터 다시 되돌아오는 노드를 찾으려면 진출차수와 SCC를 살펴보면 된다.

풀이

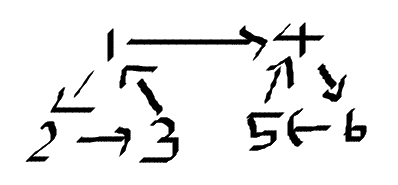
만약 이런 방향 그래프가 있다고 생각해보자.
이 문제는 자신으로부터 도달할 수 있는 모든 노드로부터 다시 되돌아오는 경로가 있는 노드를 모두 찾아내는 것이다.
1번은 가능하지 않다. 1번에서는 1,2,3,4,5,6번 전부 도달 가능하지만, 4,5,6번에서 되돌아올 수 없다.
4번은 가능하다. 4번에서는 4,5,6번에 전부 도달 가능하며 다시 되돌아올 수 있기 때문이다.
뭔가 감이 오지 않는가?
이 그래프에서 SCC로 묶는다면? 1-2-3번이 묶이고, 4-5-6번이 묶여서 SCC를 이룬다.
그러면 SCC로 방향 그래프를 나타낸다면? (1-2-3) -> (4-5-6) 으로 표현되는 DAG가 된다. 결국, SCC DAG에서 진출차수가 0인 SCC. 즉, 진출차수가 0인 SCC에 포함되는 모든 노드가 답이 되는 것이다.

BOJ 4196 도미노 풀이와 굉장히 유사하다.
다른 점은, 진입차수냐 진출차수냐이다. 잘 이해가 가지 않는다면 도미노 풀이도 참고하도록 하자.

코드

# 코사리주
import sys; input = sys.stdin.readline
sys.setrecursionlimit(100000)

def dfs(here):
    visited[here] = True
    for there in graph[here]:
        if not visited[there]:
            dfs(there)
    queue.append(here)

def reverse_dfs(here):
    visited[here] = True
    ids[here] = idx
    # 찾은 SCC를 따로 묶지 않아도 되므로 밑줄 생략
    # scc.append(here)
    for there in reverse_graph[here]:
        if not visited[there]:
            reverse_dfs(there)

while True:
    try:
        n, m = map(int, input().split())
    except:
        break
    # 간선의 수가 0이면 모든 노드가 진출차수가 0인 노드이자 SCC가 된다.
    if not m:
        input()
        print(*range(1, n + 1))
        continue
    edges = list(map(int, input().split()))
    graph = [[] for _ in range(n + 1)] # 그래프
    reverse_graph = [[] for _ in range(n + 1)] # 역방향 그래프
    for i in range(0, m * 2, 2):
        graph[edges[i]].append(edges[i + 1])
        reverse_graph[edges[i + 1]].append(edges[i])

    # 정방향 탐색으로 정점 쌓기
    visited = [False] * (n + 1)
    queue = []
    for here in range(1, n + 1):
        if not visited[here]:
            dfs(here)
    # 역방향 탐색으로 SCC 찾기
    visited = [False] * (n + 1)
    ids = [-1] * (n + 1)
    idx = 0
    while queue:
        here = queue.pop()
        if not visited[here]:
            reverse_dfs(here)
            idx += 1

    # SCC로 이루어진 DAG를 이용하여 진출차수를 모든 SCC에 대해 구하자.
    out = [0] * idx # 진출차수 배열을 SCC 개수만큼 만들고
    for here in range(1, n + 1): # 모든 정점에 대해
        for there in graph[here]: # 이어진 정점을 검사 (정방향 그래프)
            if ids[here] != ids[there]: # 만약 두 정점의 SCC 번호가 다르면
                out[ids[here]] += 1 # 진출하는 정점의 SCC의 진출차수를 증가시킨다.
    # 진출차수가 0인 SCC에 포함되어 있는 노드 번호가 정답이 된다.
    result = []
    for here in range(1, n + 1):
        if not out[ids[here]]:
            result.append(here)
    print(*result)

여담

얼른 2-sat 공부해야 하는데.. 손이 안간다. 언뜻 봤는데 복잡해보였다. 논리 연산자가 막 섞여있는..? 어후 수학 싫어