BOJ 10346 - The Maze Makers 풀이
(2024.05.10 기준 G2)

문제

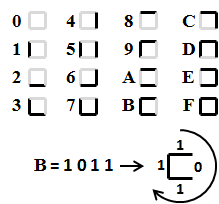
다음과 같은 규칙으로 설명하는 미로가 하나 주어진다. 주어지는 미로의 상태를 출력

알고리즘

비트마스킹을 이용해 미로를 그래프로 나타내고, DFS로 그래프 탐색

풀이

주어지는 칸의 상태에 따라 그래프를 만들자. 이는 지문 그대로 구현만 해주면 된다.

NO SOLUTION, UNREACHABLE CELL 상태인 경우는 판별하기 쉽다. 그냥 시작점에서 그래프 탐색을 하면 된다.

하지만 조금 생각이 필요한 상태는 MULTIPLE PATHS.
일단 시작점에서 도착점까지 도달할 수 있는 상태라 가정하자. 그리고 단순 경로가 $2$개 이상이 된다면, 반드시 사이클이 생긴다. 단순 경로는 경로 상에 반복되는 정점이 없어야 하므로, 이 경로가 $2$개 이상이 된다면 반드시 어느 한 정점에서 찢어져서 다른 한 정점에서 합쳐진다. 이는 결국 사이클을 이루게 된다.

코드

• C++

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 2500, di[4] = {0, 1, 0, -1}, dj[4] = {-1, 0, 1, 0};

set<int> G[MAXN]; // 간선 중복을 막기 위해 set을 사용
bool visited[MAXN];

void dfs1(int u){
    visited[u] = true;
    for (int v: G[u]) if (!visited[v]) dfs1(v);
}

bool dfs2(int u, int p){
    visited[u] = true;
    for (int v: G[u]){
        if (v == p) continue;
        if (visited[v] || dfs2(v, u)) return true;
    }
    return false;
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    int H, W;
    vector<string> S;
    for (cin >> H >> W; H; cin >> H >> W){
        S.resize(H);
        for (int i = 0; i < H; i++) cin >> S[i];

        int N = H * W, st = -1, en = -1;
        for (int i = 0; i < N; i++) G[i].clear();
        for (int i = 0; i < H; i++) for (int j = 0; j < W; j++){
            int u = i * W + j, d;
            if (S[i][j] >= 'A') d = 10 + S[i][j] - 'A';
            else d = S[i][j] - '0';
            for (int k = 0; k < 4; k++) if (!(d & (1 << k))){
                int ni = i + di[k], nj = j + dj[k];
                int v = ni * W + nj;
                if (0 <= ni && ni < H && 0 <= nj && nj < W){ // 다음 정점이 범위 안이면 간선 추가
                    G[u].insert(v);
                    G[v].insert(u);
                }
                else{ // 범위를 벗어나면 출발점 또는 도착점이 된다.
                    if (~st) en = u;
                    else st = u;
                }
            }
        }

        // 일단 도달할 수 있는 정점을 모두 찾는다.
        memset(visited, false, sizeof(visited));
        dfs1(st);
        if (!visited[en]){ // 도착점에 도달할 수 없는 경우
            cout << "NO SOLUTION\n";
            continue;
        }

        bool unreachable = false;
        for (int i = 0; i < N; i++) if (!visited[i]){ // 단 하나의 정점에라도 도달할 수 없는 경우
            unreachable = true;
            break;
        }
        if (unreachable){
            cout << "UNREACHABLE CELL\n";
            continue;
        }

        // 도착점까지 도달할 수 있음과 동시에 여러 경로가 생기는 경우는 사이클이 존재함과 동치다.
        memset(visited, false, sizeof(visited));
        if (dfs2(st, -1)) cout << "MULTIPLE PATHS\n";
        else cout << "MAZE OK\n";
    }
}

• Python

import sys; input = sys.stdin.readline
sys.setrecursionlimit(3333)
di = [0, 1, 0, -1]
dj = [-1, 0, 1, 0]

def dfs1(u):
    visited[u] = True
    for v in G[u]:
        if not visited[v]:
            dfs1(v)

def dfs2(u, p):
    visited[u] = True
    for v in G[u]:
        if v == p:
            continue
        if visited[v] or dfs2(v, u):
            return True
    return False

while True:
    H, W = map(int, input().split())
    if not H:
        break
    S = [input().strip() for _ in range(H)]

    N = H * W
    G = [set() for _ in range(N)] # 간선 중복을 막기 위해 set을 사용
    st = en = -1
    for i in range(H):
        for j in range(W):
            u = i * W + j
            d = int(S[i][j], 16)
            for k in range(4):
                if not d & (1 << k):
                    ni = i + di[k]; nj = j + dj[k]
                    v = ni * W + nj 
                    if 0 <= ni < H and 0 <= nj < W: # 다음 정점이 범위 안이면 간선 추가
                        G[u].add(v)
                        G[v].add(u)
                    else: # 범위를 벗어나면 출발점 또는 도착점이 된다.
                        if ~st:
                            en = u
                        else:
                            st = u

    # 일단 도달할 수 있는 정점을 모두 찾는다.
    visited = [False] * N
    dfs1(st)
    if not visited[en]: # 도착점에 도달할 수 없는 경우
        print('NO SOLUTION')
        continue

    unreachable = False
    for i in range(N):
        if not visited[i]: # 단 하나의 정점에라도 도달할 수 없는 경우
            unreachable = True
            break
    if unreachable:
        print('UNREACHABLE CELL')
        continue

    # 도착점까지 도달할 수 있음과 동시에 여러 경로가 생기는 경우는 사이클이 존재함과 동치다.
    visited = [False] * N
    if dfs2(st, -1):
        print('MULTIPLE PATHS')
    else:
        print('MAZE OK')