BOJ 10775 - 공항 링크
(2023.12.20 기준 G2)
문제
공항에 1~G 번호를 가진 G개의 게이트가 있고, P개의 비행기가 있다.
각 비행기에는 1~g 범위가 있으며, 이 범위에 있는 게이트 중 하나에 영구적으로 도킹해야 한다.
비행기 순서대로 최대한 도킹을 하려고 하는데, 만약 한 비행기가 도킹을 실패한다면, 이후 어떤 비행기도 도킹할 수 없게끔 공항이 폐쇄된다.도킹할 수 있는 최대 비행기 수 출력
알고리즘
그리디적으로 접근하는 분리 집합 문제
풀이
각 비행기는 [1, g] 범위를 가지고 있다. 그 범위 중 하나에 들어가야 한다.
비행기 10대가 g : 10 ~ 1로 차례대로 주어진다고 생각해보자. 차례대로 10번부터 1번까지 들어가면 10대가 전부 도킹이 가능하다. 하지만 비행기 하나라도 순서에 맞게 들어가지 않으면 10대가 전부 도킹이 되지 않는다. 왜냐 하면, 모든 범위는 1번부터 중복되게끔 주어지므로, 범위가 넓을 수록 뒷 번호에 자기만 쓸 수 있는 게이트가 생기는 것이다.
그러므로 가능한 범위 중 최대한 뒷번호에 도킹해야 한다.근데 도킹 가능한 게이트를 찾기 위해 g번, g-1번, ..., 2번, 1번 확인을 하면 TLE다.
그래서 분리 집합을 이용해보자.
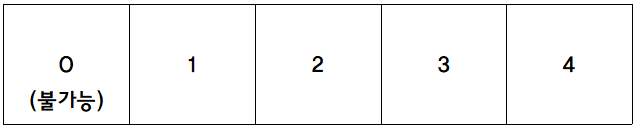
게이트 4개를 가진 공항이 있다고 생각해보자.
여기에 g = 2, 4인 비행기 2대를 도킹 시도를 할 것이다.
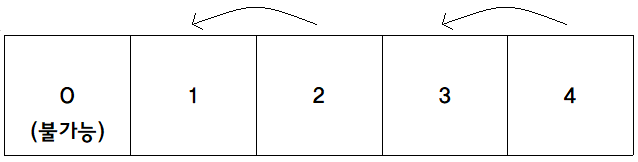
게이트 2, 4번에는 비행기가 도킹되었다. 그래서 앞으로 게이트 2번과 4번에 도킹 시도를 하면 즉시 1번과 3번에 도킹 시도를 하게끔 1번과 3번을 가리키게 했다.
다음은 g = 4인 비행기 1대를 도킹 시도를 한다.
게이트 4번은 3번을 가리키고 있었다. 그러므로 비행기는 게이트 3번에 도킹된다.
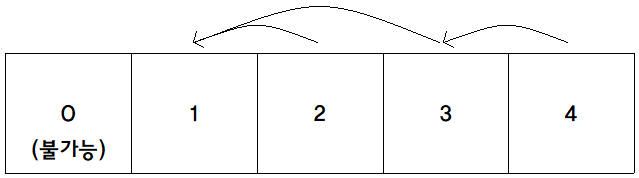
이제 3번 게이트는 2번 게이트를 가리키게 되는데, 2번 게이트는 1번 게이트를 가리키고 있었다.
그러므로 3번 게이트는 2번 게이트의 가리키는 게이트인 1번 게이트를 가리키게 된다. 그러므로 2, 3, 4번 게이트에 도킹 시도를 하면 즉시, 1번 게이트에 도킹 시도를 하게끔 되었다.
이제 g = 4인 비행기 1대를 또 도킹 시도를 해보자.
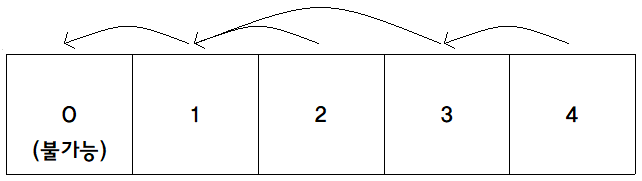
게이트 4번은 화살표를 따라 1번을 가리키고 있었고, 비행기는 1번을 가리키게 된다. 게이트 1번은 0번을 가리키게 되었다.
0번은 불가능하다는 의미로 판단하면 된다. 모든 게이트는 화살표를 따라 0번을 가리키게 되었고, 실제로 모든 게이트에 비행기가 찼다.
위 과정에서의 화살표는 곧, 분리 집합에서의 부모 배열이 된다.
따라서, find(g)가 0이 아니면 도킹 성공이며 union(find(g-1), find(g))를 하면 되고
find(g)가 0이면 도킹 실패이므로 곧바로 종료하고 지금까지 도킹을 성공한 비행기 수를 출력하면 된다.
코드
- C++
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 1;
int pa[MAXN];
int find(int u){
if (pa[u] != u) pa[u] = find(pa[u]);
return pa[u];
}
void merge(int u, int v){ // v를 u에 속하게 한다.
pa[v] = u;
}
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
int G, P; cin >> G >> P;
// 0 : 불가능, 1 ~ G : 게이트
iota(pa, pa + G + 1, 0);
int result = 0;
// 최대한 뒷 번호 게이트에 비행기를 도킹해야 한다.
// 비행기가 도킹된 게이트 i번은 i-1번을 가리키게 하고
// 게이트의 루트가 0번이 되면 불가능하다고 판단하자.
for (int g; P; P--){
cin >> g;
g = find(g);
if (g){
merge(find(g - 1), g);
result++;
}
else break;
}
cout << result;
}- Python
import sys; input = sys.stdin.readline
sys.setrecursionlimit(100000)
def find(u):
if pa[u] != u:
pa[u] = find(pa[u])
return pa[u]
def union(u, v): # v를 u에 속하게 한다.
pa[v] = u
G = int(input())
P = int(input())
# 0 : 불가능, 1 ~ G : 게이트
pa = [i for i in range(G + 1)]
result = 0
# 최대한 뒷 번호 게이트에 비행기를 도킹해야 한다.
# 비행기가 도킹된 게이트 i번은 i-1번을 가리키게 하고
# 게이트의 루트가 0번이 되면 불가능하다고 판단하자.
for _ in range(P):
g = find(int(input()))
if g:
union(find(g - 1), g)
result += 1
else:
break
print(result)