BOJ 10891 - Cactus? Not cactus? 링크
(2023.06.21 기준 P3)
문제
주어진 그래프가 정점 선인장이면 "Cactus", 아니면 "Not cactus" 출력
알고리즘
선인장을 구하기 위해 BCC를 구해보자.
풀이
선인장의 조건은 다음과 같다.
1. 간선이 3개 이상인 BCC의 정점 개수와 간선 개수가 일치해야 한다.
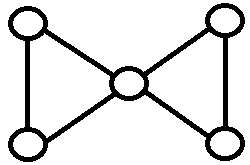
2. 정점 선인장이면 모든 단절점에 대해서 하나의 단절점은 2개 이상의 '간선이 3개 이상인 BCC'에 속할 수 없다.선인장의 사이클 형태는 단순 사이클 형태이어야 하므로 1번과 같은 조건이 생긴다.
그리고 위 그래프 그림을 보면 중앙의 점은 자기 자신으로 돌아오는 경로가 2개이다. 이처럼 정점 선인장은 1번 조건만 만족한다고 되지 않고, 2번 조건까지 만족해야 하는 것이다.이 문제는 정점 선인장에 대한 문제이므로 먼저 BCC(이중 연결 요소)를 구한 뒤, 위 두 조건을 따져서 선인장인지 확인할 수 있다.
BCC는 SCC와 굉장히 유사하다. 구하는 방법도 거의 코사리주와 비슷하다.
간략히 설명하자면, DFS 스패닝 트리를 이용해 '방문 순서의 최솟값을 반환하고 진행하면서 간선이 중복되지 않게 스택에 쌓아가는 DFS'의 결과가 현재 정점의 방문 순서보다 같거나 나중이라면 이는 현재 정점의 조상 정점으로 가지 못한다는 뜻. 즉, BCC를 이루고 있다는 뜻이다. BCC를 발견하면 현재 정점에서 진행되는 간선을 찾을 때까지 스택에서 빼내면서 저장하고, 저장된 간선들은 하나의 BCC를 이루게 된다.
코드
- C++
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int MAXN = 100000;
int lv[MAXN];
bool is_cut[MAXN];
stack<pii> stk;
vector<int> graph[MAXN];
vector<vector<pii>> bcc;
// biconnected component
int dfs(int i, int p){
int result = lv[i];
for (auto j: graph[i]){
if (j == p) continue;
// i-j 간선이 사용되지 않았다면 스택에 추가
if (lv[i] > lv[j]) stk.push({i, j});
// j가 방문하지 않은 정점이라면
if (lv[j] == -1){
lv[j] = lv[i] + 1;
int nxt = dfs(j, i);
// j로의 dfs 결과가 dfs 스패닝 트리 상 i의 조상 정점으로 갈 수 없다는 결과라면
// 새 BCC를 발견한 것이다.
if (nxt >= lv[i]){
is_cut[i] = true; // i는 단절점
vector<pii> bcc_element; // 발견한 BCC를 이루는 간선을 저장할 것이다.
pii find = {i, j}; // BCC의 첫 간선을 찾아나가야 한다.
while (!stk.empty() && stk.top() != find){ // 간선을 찾을 때까지 빼내서 저장
bcc_element.push_back(stk.top()); stk.pop();
}
bcc_element.push_back(stk.top()); stk.pop();
bcc.push_back(bcc_element); // 저장된 간선들은 BCC를 이룬다.
}
result = min(result, nxt);
}
else result = min(result, lv[j]); // 역방향 간선은 방문 순서만 따로 결과랑 비교
}
return result;
}
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
int N, M; cin >> N >> M;
for (int i = 0, x, y; i < M; i++){
cin >> x >> y;
graph[--x].push_back(--y);
graph[y].push_back(x);
}
fill(lv, lv + N, -1);
fill(is_cut, is_cut + N, false);
for (int i = 0; i < N; i++) if (lv[i] == -1){
lv[i] = 0;
dfs(i, -1);
}
// 단절점이 포함된 BCC의 번호 저장
int include[N]; fill(include, include + N, -1);
for (int i = 0, n = bcc.size(); i < n; i++){
// 간선 개수가 1이면 사이클이 생기지 않는다.
if (bcc[i].size() == 1) continue;
vector<int> vertex; // BCC를 이루는 정점 번호 저장
for (auto [x, y]: bcc[i]){
// 각 정점이 만약 단절점이면 현재 BCC의 번호를 저장한다.
// 만약 현재 BCC가 아닌 다른 BCC의 번호가 저장되어 있다면 선인장이 아니다.
if (is_cut[x]){
if (include[x] == -1 || include[x] == i) include[x] = i;
else{
cout << "Not cactus";
return 0;
}
}
if (is_cut[y]){
if (include[y] == -1 || include[y] == i) include[y] = i;
else{
cout << "Not cactus";
return 0;
}
}
vertex.push_back(x); vertex.push_back(y);
}
// 저장된 정점들의 중복을 제거한 후
// 정점 개수와 간선 개수가 일치하는지 확인
sort(vertex.begin(), vertex.end());
vertex.erase(unique(vertex.begin(), vertex.end()), vertex.end());
if (vertex.size() != bcc[i].size()){
cout << "Not cactus";
return 0;
}
}
cout << "Cactus";
}- Python
import sys; input = sys.stdin.readline
sys.setrecursionlimit(100000)
# biconnected component
def dfs(i, p):
result = lv[i]
for j in graph[i]:
if j == p:
continue
# i-j 간선이 사용되지 않았다면 스택에 추가
if lv[i] > lv[j]:
stk.append((i, j))
# j가 방문하지 않은 정점이라면
if lv[j] == -1:
lv[j] = lv[i] + 1
nxt = dfs(j, i)
# j로의 dfs 결과가 dfs 스패닝 트리 상 i의 조상 정점으로 갈 수 없다는 결과라면
# 새 BCC를 발견한 것이다.
if nxt >= lv[i]:
is_cut[i] = True # i는 단절점
bcc_element = [] # 발견한 BCC를 이루는 간선을 저장할 것이다.
find = (i, j) # BCC의 첫 간선을 찾아나가야 한다.
while stk and stk[-1] != find:
bcc_element.append(stk.pop())
bcc_element.append(stk.pop())
bcc.append(bcc_element) # 저장된 간선들은 BCC를 이룬다.
result = min(result, nxt)
else: # 역방향 간선은 방문 순서만 따로 결과랑 비교
result = min(result, lv[j])
return result
N, M = map(int, input().split())
graph = [[] for _ in range(N)]
for _ in range(M):
x, y = map(int, input().split())
x -= 1; y -= 1
graph[x].append(y)
graph[y].append(x)
lv = [-1] * N
is_cut = [False] * N
bcc = []; stk = []
for i in range(N):
if lv[i] == -1:
lv[i] = 0
dfs(i, -1)
# 단절점이 포함된 BCC의 번호 저장
include = [-1] * N
for i in range(len(bcc)):
# 간선 개수가 1이면 사이클이 생기지 않는다.
if len(bcc[i]) == 1:
continue
vertex = [] # BCC를 이루는 정점 번호 저장
for x, y in bcc[i]:
# 각 정점이 만약 단절점이면 현재 BCC의 번호를 저장한다.
# 만약 현재 BCC가 아닌 다른 BCC의 번호가 저장되어 있다면 선인장이 아니다.
if is_cut[x]:
if include[x] == -1 or include[x] == i:
include[x] = i
else:
print('Not cactus')
exit()
if is_cut[y]:
if include[y] == -1 or include[y] == i:
include[y] = i
else:
print('Not cactus')
exit()
vertex.append(x); vertex.append(y)
# 저장된 정점들의 중복을 제거한 후
# 정점 개수와 간선 개수가 일치하는지 확인
if len(set(vertex)) != len(bcc[i]):
print('Not cactus')
exit()
print('Cactus')여담
마지막에 선인장인지 확인할 때를 위해 is_cut, include, vertex를 사용했지만, 정점이 BCC에 사용됐는지 확인할 bool 배열만 있어도 가능하다. 단절점이 아닌 이상 정점은 한번만 쓰이게 되고, 단절점이 사이클을 이루는 BCC에 여러 번 사용된다면 자연스럽게 판별이 될 것이기 때문.
다만, 아직 이중 연결 요소와 선인장에 대한 문제를 접한지 얼마 되지 않았고, 블로그에도 이중 연결 요소와 선인장에 대한 글을 처음 쓰기 때문에, 아주 정직하게 코드를 짜보았다.
나중에 MLE가 나거나 BCC에 대한 숙련도가 많이 쌓이면 저렇게 해야겠다.