BOJ 11106 - Free Willy 링크
(2024.04.08 기준 P3)

문제

길이 $N$인 문자열 $S$, 문자열 $T$, 영어 소문자로 이루어진 순열 $P$개가 주어진다.
$L$회 이내에 $S$에 순열을 적용시켜 $T$로 변환할 수 있는지 판별

알고리즘

상태를 최대한 줄이는 양방향 탐색

풀이

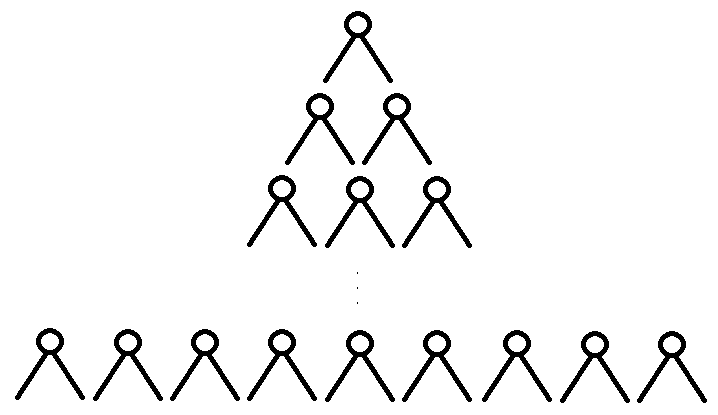
$S$를 시작 정점, $T$를 도착 정점으로 한 그래프라고 생각해보자. 시작 정점에서 도착 정점까지의 거리가 $L$이라고 했을 때, early cut을 한다해도 방문하는 정점은 최대 $P^L$개이다. 이를 모두 방문하면 당연히 TLE가 난다.

시작 정점에서 탐색을 시작하면 위 그림과 같이 탐색을 할 것이다.

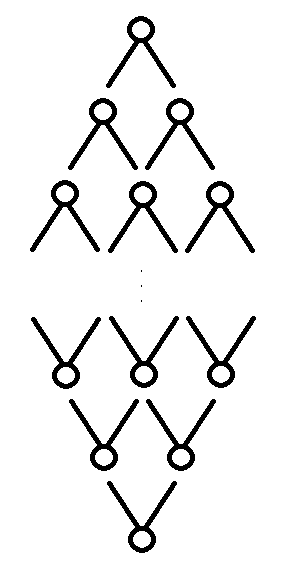
그런데 만약 시작 정점과 도착 정점에서 동시에 탐색을 시작하면?

직관적으로 방문하는 상태를 줄일 수 있음을 알 수 있다. 깊이를 각각 $L/2$까지만 탐색하면 되기 때문에, 시간 복잡도는 $O(P^{L / 2})$로 줄일 수 있게 된다.

그럼 이제 양방향 탐색이란 것을 어떻게 하느냐.
시작 정점에서의 탐색을 정방향, 도착 정점에서의 탐색을 역방향이라고 해보자. 정방향은 양수로, 역방향은 음수로 거리를 계산하면서 탐색을 진행하자. 그러다가 부호가 다른 거리끼리 만난다면? 그 길이 바로 시작 정점과 도착 정점까지의 최단거리가 되는 것이다.

코드

• C++

#include <bits/stdc++.h>
using namespace std;

void solve(){
    int N, P, L; cin >> N >> P >> L;
    string A, B; cin >> A >> B;
    string perms[P]; for (int i = 0; i < P; i++) cin >> perms[i];

    // 두 문자열이 같으면 0 출력
    if (A == B){
        cout << 0 << '\n';
        return;
    }

    // 양방향 탐색
    queue<string> q;
    map<string, int> dist; // 문자열 자체를 정점으로 나타내기 위해 해시 맵 사용
    q.push(A); dist[A] = 1; // 정방향은 양수
    q.push(B); dist[B] = -1; // 역방향은 음수

    while (!q.empty()){
        string s = q.front(); q.pop();

        // 만나더라도 무조건 L 초과이면 더이상 탐색하는 의미가 없다.
        if (abs(dist[s]) * 2 - 1 > L){
            cout << "whalemeat\n";
            return;
        }

        for (string p: perms){
            string nxt; nxt.resize(N); // 다음 문자열
            if (dist[s] > 0){ // 정방향 탐색일 경우 순열을 그대로 적용
                for (int i = 0; i < N; i++) nxt[i] = s[p[i] - 97];
            }
            else{ // 역방향 탐색일 경우 순열을 거꾸로 적용
                for (int i = 0; i < N; i++) nxt[p[i] - 97] = s[i];
            }

            // 다음 문자열을 방문한 적이 있다면, 현재 탐색 방향과 방향을 비교해본다.
            // 만약 서로 다른 방향이라면 중간에서 만난 것이다.
            if (dist[nxt]){
                if ((dist[s] > 0 && dist[nxt] < 0) || (dist[s] < 0 && dist[nxt] > 0)){
                    int res = abs(dist[s]) + abs(dist[nxt]) - 1;
                    if (res <= L) cout << res << '\n';
                    else cout << "whalemeat\n";
                    return;
                }
            }

            // 다음 문자열을 방문한 적이 없다면, 현재 탐색 방향으로 저장한다.
            else{
                q.push(nxt);
                if (dist[s] > 0) dist[nxt] = dist[s] + 1;
                else dist[nxt] = dist[s] - 1;
            }
        }
    }

    // 출력을 하지 않고 탐색이 종료되면 A와 B가 서로 만날 수 없다는 뜻이다.
    cout << "whalemeat\n";
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    int T; cin >> T;
    while (T--) solve();
}

• Python

import sys; input = sys.stdin.readline
from collections import defaultdict, deque

def solve():
    N, P, L = map(int, input().split())
    A, B = input().split()
    perms = [input().strip() for _ in range(P)]

    # 두 문자열이 같으면 0 출력
    if A == B:
        print(0)
        return

    # 양방향 탐색
    dq = deque([A, B])
    dist = defaultdict(int) # 문자열 자체를 정점으로 나타내기 위해 해시 맵 사용
    dist[A] = 1; dist[B] = -1 # 정방향은 양수, 역방향은 음수

    while dq:
        s = dq.popleft()

        # 만나더라도 무조건 L 초과이면 더이상 탐색하는 의미가 없다.
        if abs(dist[s]) * 2 - 1 > L:
            print('whalemeat')
            return

        for p in perms:
            nxt = ['' for _ in range(N)] # 다음 문자열
            if dist[s] > 0: # 정방향 탐색일 경우 순열을 그대로 적용
                for i in range(N):
                    nxt[i] = s[ord(p[i]) - 97]
            else: # 역방향 탐색일 경우 순열을 거꾸로 적용
                for i in range(N):
                    nxt[ord(p[i]) - 97] = s[i]
            nxt = ''.join(nxt)

            # 다음 문자열을 방문한 적이 있다면, 현재 탐색 방향과 방향을 비교해본다.
            # 만약 서로 다른 방향이라면 중간에서 만난 것이다.
            if dist[nxt]:
                if (dist[s] > 0 and dist[nxt] < 0) or (dist[s] < 0 and dist[nxt] > 0):
                    res = abs(dist[s]) + abs(dist[nxt]) - 1
                    print(res if res <= L else 'whalemeat')
                    return

            # 다음 문자열을 방문한 적이 없다면, 현재 탐색 방향으로 저장한다.
            else:
                dq.append(nxt)
                if dist[s] > 0:
                    dist[nxt] = dist[s] + 1
                else:
                    dist[nxt] = dist[s] - 1

    # 출력을 하지 않고 탐색이 종료되면 A와 B가 서로 만날 수 없다는 뜻이다.
    else:
        print('whalemeat')
    
for _ in range(int(input())):
    solve()