BOJ 13421 - 국민 랜드 링크
(2023.04.05 기준 G2)

문제

임의의 네 점이 주어진다.
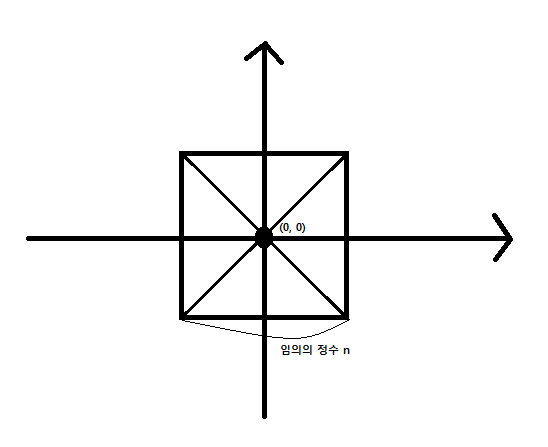
'한 변의 길이가 정수이며 각 변은 x축 또는 y축과 평행하며 두 대각선의 교점이 (0, 0)인 정사각형' 중에서 각 꼭짓점과 임의의 네 점을 하나씩 연결했을 때의 총 맨해튼 거리의 합이 최소화가 되는 정사각형의 변의 길이 출력.

알고리즘

삼분 탐색

풀이

아무 네 점을 떠올려 보자. 그리고 아주 큰 정사각형부터 아주 작은 정사각형까지 줄여나가면서 상상을 해보자.
점끼리 연결하는 맨해튼 거리의 합이 점점 줄어들다가 다시 어느 순간 늘어난다.
결국 변의 길이에 따른 맨해튼 거리의 합을 나타내는 함수는 밑으로 볼록한 볼록 함수이다.

볼록 함수에서의 최적값을 찾기 위해선? 삼분 탐색이다.

그리고 당연하지만, 교점이 (0, 0)이고 변이 축과 평행하면?

이런 모양이다. 결국 정사각형의 네 점의 x, y 좌표의 절댓값은 전부 같다.

주의사항

예.. 조심하자구요.. 난 저거 못보고 맞왜틀 계속 시전함.

코드

• C++

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const ld inf = 1e16;

int sign[4][2] = {{-1, -1}, {-1, 1}, {1, -1}, {1, 1}}; // 왼쪽 밑, 왼쪽 위, 오른쪽 밑, 오른쪽 위
ll pos[4][2];

ld f(ld x){
    ld y = inf, result;
    /**
    permutaion : 정사각형의 네 점과 짝 지을 수 있는 모든 경우의 수
    모든 경우의 수마다 결과를 구해 가장 작은 값 반환
    **/
    vector<int> permutaion = {0, 1, 2, 3};
    do{
        result = 0;
        for (int i = 0; i < 4; i++) result += fabs(pos[permutaion[i]][0] - sign[i][0] * x) + fabs(pos[permutaion[i]][1] - sign[i][1] * x);
        y = min(y, result);
    }
    while (next_permutation(permutaion.begin(), permutaion.end()));
    return y;
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    for (int i = 0; i < 4; i++) cin >> pos[i][0] >> pos[i][1];

    ll st = 1, en = 2000000000, m1, m2; // 좌표의 절댓값 범위는 최대 1,000,000,000.
    while (en - st >= 3){ // 차이가 3 이상인 동안만
        m1 = (st * 2 + en) / 3;
        m2 = (st + en * 2) / 3;
        if (f((ld)m1 / 2) < f((ld)m2 / 2)) en = m2; // 정사각형의 절댓값 좌표는 '변의 길이 / 2'가 된다.
        else st = m1;
    }

    int answer = -1;
    ld result = inf, y;
    for (int x = st; x <= en; x++){ // 찾아낸 [start, end] 구간에서 최솟값을 가진 최대 변의 길이를 찾자.
        y = f((ld)x / 2);
        if (result > y || fabs(result - y) < 1e-9) answer = x, result = y; // result >= y 이지만 소수점 오차 고려
    }

    cout << answer;
}

• Python

import sys; input = sys.stdin.readline
from math import inf
from itertools import permutations

def f(x):
    y = inf
    for permutation in Permutations: # 모든 경우의 수마다 결과를 구해 가장 작은 값 반환
        result = 0
        for i in range(4):
            result += abs(pos[permutation[i]][0] - sign[i][0] * x) + abs(pos[permutation[i]][1] - sign[i][1] * x)
        y = min(y, result)
    return y

pos = [list(map(int, input().split())) for _ in range(4)]
Permutations = list(permutations([i for i in range(4)])) # 정사각형의 네 점과 짝 지을 수 있는 모든 경우의 수
sign = [(-1, -1), (-1, 1), (1, -1), (1, 1)] # 왼쪽 밑, 왼쪽 위, 오른쪽 밑, 오른쪽 위

start = 1; end = 2000000000 # 좌표의 절댓값 범위는 최대 1,000,000,000.
while end - start >= 3: # 차이가 3 이상인 동안만
    mid_1 = (start * 2 + end) // 3
    mid_2 = (start + end * 2) // 3
    if f(mid_1 / 2) < f(mid_2 / 2): # 정사각형의 절댓값 좌표는 '변의 길이 / 2'가 된다.
        end = mid_2
    else:
        start = mid_1

answer = -1
result = inf
for x in range(start, end + 1): # 찾아낸 [start, end] 구간에서 최솟값을 가진 최대 변의 길이를 찾자.
    y = f(x / 2)
    print(x, y)
    if result > y or abs(result - y) < 1e-9: # result >= y 이지만 소수점 오차 고려
        answer = x
        result = y
print(answer)