BOJ 15576 - 큰 수 곱셈 (2) 링크
(2023.04.19 기준 P1)

문제

수의 길이가 최대 300,000인 음이 아닌 두 정수가 주어질 때, 두 정수의 곱 출력

알고리즘

그냥 곱셈은 O(N^2) 이므로 TLE. O(NlgN)인 FFT를 이용하여 곱셈을 해보자.

풀이

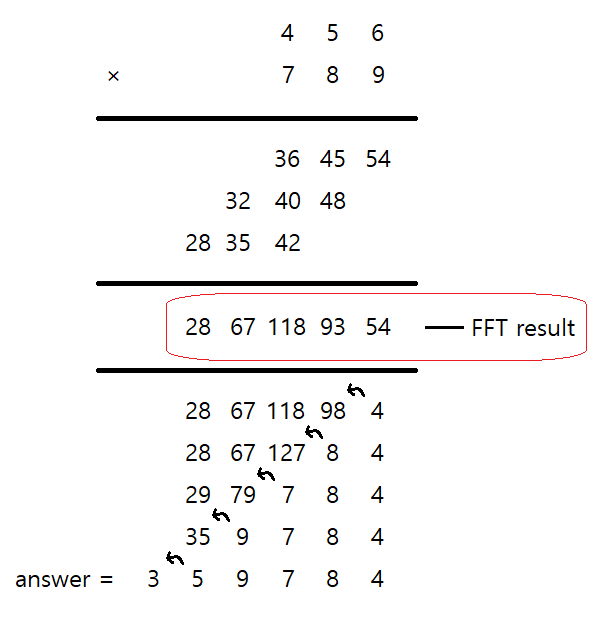
FFT의 결과는 각 수의 자릿수마다의 곱셈 결과의 합이다.
456 * 789를 예로 들면,

위와 같이 된다.
이 때, FFT의 결과는 그림의 빨간 박스가 된다.
그렇다면 이제 일의 자리부터 올림 처리만 직접 해주면 된다.

코드

• C++

#include <bits/stdc++.h>
#define _USE_MATH_DEFINES
using namespace std;
typedef complex<double> cpx;

// 거듭제곱을 이용한 FFT
void fft(vector<cpx> &A, bool inv = false){
    int n = A.size();
    for (int i = 1, j = 0, bit; i < n; i++){
        bit = n >> 1;
        while (j >= bit) j -= bit, bit >>= 1;
        j += bit;
        if (i < j) swap(A[i], A[j]);
    }

    double p = M_PI;
    if (inv) p *= -2; else p *= 2;
    for (int s = 2; s <= n; s <<= 1){
        cpx z = exp((cpx){0, p / s});
        for (int i = 0; i < n; i += s){
            cpx w = {1, 0};
            for (int j = i; j < i + (s >> 1); j++){
                cpx tmp = A[j + (s >> 1)] * w;
                A[j + (s >> 1)] = A[j] - tmp;
                A[j] += tmp;
                w *= z;
            }
        }
    }

    if (inv) for (auto &x: A) x /= n;
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    string SA, SB;
    cin >> SA >> SB;

    // 필요한 길이(a + b - 1)보다 크면서, 가장 작은 2의 거듭제곱
    int a = SA.size(), b = SB.size(), N = 1 << (int)ceil(log2(a + b - 1));

    // 거듭제곱을 이용한 FFT를 위해 길이를 2의 거듭제곱이 되게끔 맞춘다.
    vector<cpx> A(N, {0, 0});
    for (int i = 0; i < a; i++) A[i] = {SA[i] - '0', 0};
    vector<cpx> B(N, {0, 0});
    for (int i = 0; i < b; i++) B[i] = {SB[i] - '0', 0};

    // A와 B의 합성곱 구하기
    fft(A); fft(B);
    for (int i = 0; i < N; i++) A[i] *= B[i];
    fft(A, true);

    // a의 길이의 정수와 b의 길이의 정수의 곱은 최대 a + b다.
    int result[a + b] = {0, };
    for (int i = 0; i < a + b - 1; i++) result[i + 1] = round(A[i].real());

    // 올림 처리
    for (int i = a + b - 1; i > 0; i--){
        result[i - 1] += result[i] / 10;
        result[i] %= 10;
    }

    if (result[0]) cout << result[0]; // 첫 자리는 0일 수도 있다.
    for (int i = 1; i < a + b; i++) cout << result[i];
}

• Python (제출 불가)

import sys; input = sys.stdin.readline
from cmath import exp, pi
from math import ceil, log2

# 거듭제곱을 이용한 FFT
def fft(A, inv = False):
    n = len(A)
    j = 0
    for i in range(1, n):
        bit = n >> 1
        while j >= bit:
            j -= bit
            bit >>= 1
        j += bit
        if i < j:
            A[i], A[j] = A[j], A[i]

    p = (-2 if inv else 2) * pi
    s = 2
    while s <= n:
        z = exp(complex(0, p / s))
        for i in range(0, n, s):
            w = 1 + 0j
            for j in range(i, i + (s >> 1)):
                tmp = A[j + (s >> 1)] * w
                A[j + (s >> 1)] = A[j] - tmp
                A[j] += tmp
                w *= z
        s <<= 1

    if inv:
        for i in range(n):
            A[i] /= n

A, B = input().split()
A = list(map(int, A))
B = list(map(int, B))

a = len(A)
b = len(B)
N = 1 << ceil(log2(a + b - 1)) # 필요한 길이(a + b - 1)보다 크면서, 가장 작은 2의 거듭제곱

# 거듭제곱을 이용한 FFT를 위해 길이를 2의 거듭제곱이 되게끔 맞춘다.
A += [0] * (N - a)
B += [0] * (N - b)

# A와 B의 합성곱 구하기
fft(A); fft(B)
for i in range(N):
    A[i] *= B[i]
fft(A, True)

# a의 길이의 정수와 b의 길이의 정수의 곱은 최대 a + b다.
result = [0] * (a + b)
for i in range(a + b - 1):
    result[i + 1] = round(A[i].real)

# 올림 처리
for i in range(a + b - 1, 0, -1):
    result[i - 1] += result[i] // 10
    result[i] %= 10

if result[0]: # 첫 자리는 0일 수도 있다.
    print(result[0], end = '')
print(*result[1:], sep = '')