BOJ 17574 - Jackpot 링크
(2023.06.01 기준 G4)

문제

n개의 문이 있고 그 중 하나의 문 뒤에만 상금이 있다.
그 전에 먼저 d개의 문을 열어봐서 제외시킬 수 있다. 초기 상금 m, 열어본 문 d, 계수 f라고 하였을 때, d개의 문을 열어보면 상금은 m - (d · f) ^ 2 가 된다.
이 때, 상금의 기댓값 중 최댓값은?

알고리즘

수학을 곁들인 삼분 탐색

풀이

삼분 탐색을 사용하기 위해선 함수가 볼록 함수여야 한다.
열어본 문 d에 따른 상금의 기댓값은 결국 다음과 같다.

(m - (d · f) ^ 2) / (n - d)

이는 볼록 함수일까?
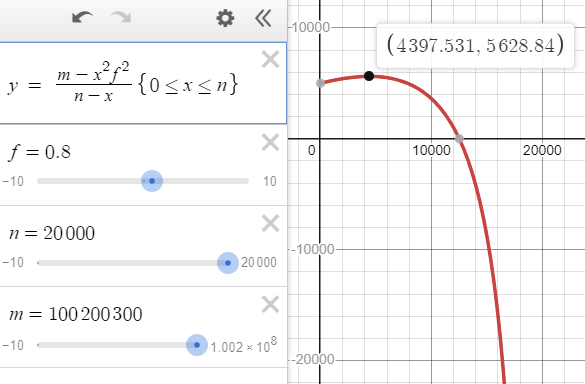
그래프 그려주는 사이트에서 확인해보면 다음과 같다.

예제 2번을 그대로 입력해보면 극값이 정답과 일치함을 볼 수 있고, 볼록 함수임을 알 수 있다.

수학자가 아니라서 저 식이 왜 볼록 함수인지 엄밀히 증명은 못하겠다만, 최고차항의 차수는 2이며 계수는 음수이므로 위로 볼록한 볼록 함수일 것이다.

코드

• C++

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

ll n, m;
double f;

double F(ll d){ // 문을 d개를 열었을 때의 상금의 기댓값
    double P = m - pow(d * f, 2);
    return P / (n - d);
}

int main(){
    cin >> n >> m >> f;

    // 열린 문의 개수 d에 따른 상금의 기댓값의 최솟값을 삼분 탐색을 통해 구한다.
    ll st = 0, en = n - 1, mid_1, mid_2; // 전부(n개)를 열면 상금은 0원이므로 n은 제외
    while (en - st >= 3){
        mid_1 = (st * 2 + en) / 3;
        mid_2 = (st + en * 2) / 3;
        if (F(mid_1) > F(mid_2)) en = mid_2;
        else st = mid_1;
    }

    // 찾아낸 [st, en] 구간에서 최댓값을 찾자.
    double result = 0;
    for (ll d = st; d <= en; d++) result = max(result, F(d));
    cout << fixed << setprecision(7) << result << '\n'; 
}

• Python

import sys; input = sys.stdin.readline

def F(d): # 문을 d개를 열었을 때의 상금의 기댓값
    P = m - (d * f) ** 2
    return P / (n - d)

n, m, f = input().split()
n = int(n); m = int(m); f = float(f)

# 열린 문의 개수 d에 따른 상금의 기댓값의 최솟값을 삼분 탐색을 통해 구한다.
st = 0; en = n - 1 # 전부(n개)를 열면 상금은 0원이므로 n은 제외
while en - st >= 3:
    mid_1 = (st * 2 + en) // 3
    mid_2 = (st + en * 2) // 3
    if F(mid_1) > F(mid_2):
        en = mid_2
    else:
        st = mid_1

# 찾아낸 [st, en] 구간에서 최댓값을 찾자.
print(max(F(d) for d in range(st, en + 1)))