파이썬은 편리하다. 하지만 무겁다.
그래서 편하게 풀 수 있는 문제가 있는 반면에, 쉬운 문제도 어렵게 풀어야 하는 경우도 있다.
이번 풀이는 후자에 포함되는 문제를 다뤄보겠다.
BOJ 18111 - 마인크래프트 링크
(2022.09.28 기준 S2)
(치팅하면 밤에 무서운 몬스터 만남)
문제
세로 N, 가로 M 크기의 땅이 있고 모든 땅의 높이를 일정하게 바꿔야 한다.
1. 좌표 (i, j)의 가장 위에 있는 블록을 제거하여 인벤토리에 넣는다.
2. 인벤토리에서 블록 하나를 꺼내어 좌표 (i, j)의 가장 위에 있는 블록 위에 놓는다.
두 종류의 작업을 할 수 있을 때, 가장 빨리 끝내는 시간과 그 경우의 땅의 높이를 출력
알고리즘
높이의 범위를 정하여, 그 범위 안 높이를 전부 살펴봐야 한다. 브루트포스
그리고 마인크래프트를 잘 알면 좋으니 '게임 이론' ㅋ
풀이
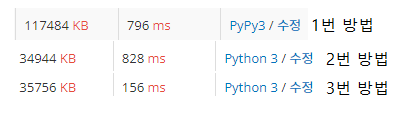
먼저 PyPy3를 포함한 웬만한 빠른 언어에서 AC를 받을 수 있는 풀이는 다음과 같다.
- 모든 높이에 대해 최소 높이, 최대 높이를 구해놓고
최대 높이에서 최소 높이로 내려가면서 모든 땅의 작업 시간을 구해 답을 갱신해나가는 것.누구나 쉽게 생각할 수 있는 풀이 방법이며, 브루트포스 알고리즘에 걸맞는 방법이라고 할 수 있다.
ans_time = ans_height = inf # 답. 초기는 inf로 for height in range(highest, lowest - 1, -1): blocks = B; time = 0 # 남은 블록, 시간 for n in range(N): for m in range(M): if matrix[n][m] < height: # 땅이 기준보다 낮으면 time += height - matrix[n][m] # 시간은 차이만큼 걸리고 blocks -= height - matrix[n][m] # 블록은 차이만큼 줄어든다. elif height < matrix[n][m]: # 땅이 기준보다 높으면 time += (matrix[n][m] - height) * 2 # 시간은 차이 * 2만큼 걸리고 blocks += matrix[n][m] - height # 블록은 차이만큼 늘어난다. if blocks >= 0 and ans_time > time: # 답 갱신. 남은 블록이 음수가 아니어야 한다. ans_time = time ans_height = height최악의 경우 시간 복잡도는 O(257 * N * M)이다. 느린 언어는 이렇게 하면 시간 초과가 날 것이다.
그럼 이제 첫번째 최적화를 해보자.
위 방법은 제일 높은 높이부터 시작했다. 그리고 블록이 부족한 높이이면 패스하는 방식.
그러면 블록이 부족하지 않은 가장 높은 높이부터 시작하면 어떨까?
먼저 인벤토리의 블록 B개와 모든 땅의 블록을 모으자. 땅을 모두 같은 높이로 고르게 만들어야 하니 모은 블록을 땅 크기인 (N * M)으로 나누면 가능한 높이 중 제일 높은 높이가 나온다.
이 높이와 제일 높은 높이 중 낮은 높이부터 시작하면 블록이 부족할 일은 절대 없는 것이다.
그러면 여기서 중요한 점. 이제부터 높이마다 탐색할 때, 답이 갱신 되지 않으면 탐색을 중단해야 한다.
높이가 낮아질수록 블록을 제거하는 작업이 더 많아지기 때문이다.
결국 요약하자면, Python3와 같은 느린 언어에서 AC를 받을 수 있는 풀이는 다음과 같다.
- 블록이 부족하지 않은 가장 높은 높이부터 시작하여 탐색하고, 답이 갱신되지 않으면 즉시 중단.
highest = min((B + 모든 땅의 블록) // (N * M), 가장 높은 땅의 높이)
이렇게 하면 웬만하면 만족하고 넘어가면 되지만.. 내가 생각한 마지막 최적화가 남아있다.
바로 Counter
이 문제는 좌표가 중요하지 않다. 땅의 높이에 따른 작업 시간만 중요할 뿐.
그러므로, 탐색 전에 모든 좌표를 한바퀴 돌아서 나오는 땅의 높이를 카운트하자. (파이썬에선 간단하게 Counter. 다른 언어는 잘 모르겠음.)
그러면 앞으로 탐색할 때, 일일히 좌표 전부를 돌 필요가 없다. 나온 땅의 높이와 나온 횟수로 작업 시간을 구해주면 된다.
요약하자면, 시간이 아주 넉넉하게끔 AC를 받을 수 있는 풀이는 다음과 같다.
- 땅의 높이를 카운트 (파이썬에선 Counter). 탐색할 때에는 땅의 높이와 나온 횟수로 작업 시간을 구하자.
2번과 3번 방법에선 웬만하면 행렬 입력을 일자로 펴서 리스트로 입력 받는 것이 편할 것이다.
코드에 주석을 달아 놓았으니 참고!
코드
import sys; input = sys.stdin.readline
from math import inf
from collections import Counter
def solve():
N, M, B = map(int, input().split())
heights = [] # 각 좌표마다의 땅의 높이를 저장. 행렬 입력을 리스트로 나타낼 것이다.
for _ in range(N):
heights += list(map(int, input().split()))
# 땅의 높이를 Counter로 저장하자.
# 좌표는 중요하지 않으므로
# 땅의 높이마다 걸리는 시간을 나온 횟수만큼 곱하면 시간 최적화가 된다.
counter = Counter(heights).items()
# 답이 될 수 있는 가장 높은 높이는 세 가지 경우 중 제일 낮은 높이다.
# 1. 땅의 높이 중 제일 높은 높이
# 2. 블록의 개수와 모든 땅의 높이 합을 합쳐 (N * M)으로 나눈, 고르게 분배한 높이
# 이 높이부터 시작하여 1씩 감소시키면서 답을 갱신해나가면 된다.
highest = min((B + sum(heights)) // (N * M), max(heights))
ans_time = ans_height = inf # 답은 초기에 inf로 설정
for height in range(highest, -1, -1):
time = 0
for h, ct in counter:
if height < h: # 땅의 높이가 기준 높이보다 높으면 블록을 제거해야 한다.
# 높이 차이만큼 블록을 제거해야 하므로 차이 * 2 * ct(나온횟수) 만큼 시간이 걸린다.
time += (h - height) * ct * 2
else: # 땅의 높이가 기준 높이보다 작으면 블록을 쌓아야 한다.
# 높이 차이만큼 블록을 쌓아야 하므로 차이 * ct(나온횟수) 만큼 시간이 걸린다.
time += (height - h) * ct
if ans_time > time: # 걸린 시간이 답보다 짧게 걸렸으면 답을 갱신
ans_time = time
ans_height = height
# 걸린 시간이 더 오래 걸렸으면 더 이상 탐색할 필요가 없다.
# 높이가 낮아질수록 블록을 제거하는 작업이 더 많아지기 때문이다.
else:
break
print(ans_time, ans_height) # 답 출력
solve()여담
이런 문제 꽤 흥미롭다.
최적화의 단계에 따라 난이도가 달라지는 기분.
이 문제를 범위를 늘리거나 시간을 줄여서 '마인크래프트 2'라는 문제로 내면... 난이도 격상할 듯..?