BOJ 20652 - Stuck in a Rut 링크
(2024.03.31 기준 G2)

문제

북쪽이나 동쪽으로 한 칸씩 이동하는 $N$마리의 소가 있다. 모든 소는 매 시간 다음과 같은 과정을 거친다.

1. 현재 있는 칸이 다른 소가 이미 지나간 칸이면 멈춘다.
2. 멈추지 않으면, 현재 있는 칸에서 풀을 뜯어먹고 다음 칸으로 이동한다.

두 마리 이상의 소가 동시에 같은 칸에 도착하면 멈추지 않고 그 칸을 공유하게 된다.

$N$마리의 소 각각 풀을 뜯어먹는 칸의 개수를 출력

알고리즘

시뮬레이션 느낌으로 구현

풀이

두 소의 길이 겹치는 경우는 두 가지가 있다.

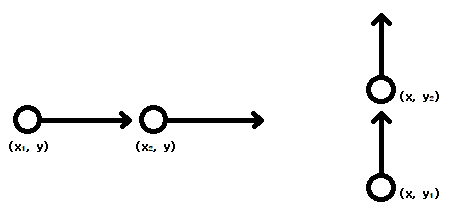
첫 번째로 두 소의 방향이 같은 경우이다. 이 경우엔 변하지 않는 좌표가 동일해야 함을 위 그림으로 한눈에 알 수 있다.

두 번째로 두 소의 방향이 다른 경우이다.
동쪽으로 가는 소의 시작 좌표를 $(x_1, y_1)$, 북쪽으로 가는 소의 시작 좌표를 $(x_2, y_2)$라고 하자. 그러면 $x_1 \le x_2$와 $y_2 \le y_1$을 만족해야 함을 위 그림으로 알 수 있다.

첫 번째 경우에는 당연히 왼쪽이나 아래쪽에 있는 소가 멈출 것이다. 하지만 두 번째 경우에는 어떻게 판별할까? 소는 다른 소가 이미 지나간 길에 도착하면 멈추게 된다. 즉, 두 소의 교차점에 늦게 도착하는 소가 멈추게 되는 것이다. 그러니 두 소의 교차점까지의 거리를 계산해서, 교차점까지의 거리가 더 먼 소가 멈추는 것이다.

위 과정을 모든 소 쌍에 대해 적용 및 계산하면 끝인걸까? 아니다. 예제로 주어지는 TC부터 막히게 된다.

위 그림을 살펴보자. $1$번 소와 $3$번 소는 $(x_3, y_1)$ 교차점을 가지며 $1$번 소가 멈춘다. $2$번 소와 $3$번 소는 $(x_3, y_2)$ 교차점을 가지며 $3$번 소가 멈춘다.

그러면 출력해야 하는 값은 각각 $x_3-x_1$, $inf$, $y_2-y_3$일까? 아니다. $3$번 소는 $1$번과의 교차점에 가기 전에 $(x_3, y_2)$에서 멈추게 된다.

어떤 소가 다른 소에 의해 멈추게 되는 것을 사건이라고 표현해보자. 사건들은 소가 움직이는 거리가 짧을수록 더 빨리 일어난다. 먼저 일어나는 사건 순으로 처리를 하면서 각 소가 어디서 멈췄는지 저장을 해두면, 두 소의 교차점까지 멈추게끔 하는 소가 정말로 오는지 확인할 수 있게 된다.

코드

• C++

#include <bits/stdc++.h>
using namespace std;

typedef tuple<int, int, int> tiii;

const int inf = INT_MAX;

struct Cow{
    // 방향, x 시작 좌표, y 시작 좌표, x 끝 좌표, y 끝 좌표, 움직이는 거리
    int d, x, y, ex, ey, dist;
    Cow(char d_, int x, int y): x(x), y(y){
        if (d_ == 'E') d = 0;
        else d = 1;
        if (d == 0) ex = inf, ey = y;
        else ex = x, ey = inf;
        dist = inf;
    }
};

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    int N; cin >> N;
    vector<Cow> cows; char d; int x, y;
    for (int i = 0; i < N; i++) cin >> d >> x >> y, cows.push_back(Cow(d, x, y));

    // 모든 소 쌍에 대해서 두 소의 길이 겹치는지 그리고 겹친다면 겹치는 점까지의 거리를 저장
    vector<tiii> events; // (거리, 멈추는 소의 번호, 멈추게끔 하는 소의 번호)
    for (int i = 0; i < N - 1; i++) for (int j = i + 1; j < N; j++){

        // 두 소의 방향이 다르다면
        if (cows[i].d ^ cows[j].d){
            // i번 소가 동쪽, j번 소가 북쪽으로 이동한다면
            // x_i <= x_j와 y_j <= y_i를 만족해야 두 소의 길이 겹친다.
            if (cows[i].d == 0){
                if (cows[i].x <= cows[j].x && cows[j].y <= cows[i].y){
                    int di = cows[j].x - cows[i].x;
                    int dj = cows[i].y - cows[j].y;
                    // 교차점까지의 거리가 먼 소가 멈추게 된다.
                    // 만약 거리가 같으면 멈추지 않는다.
                    if (di > dj) events.push_back({di, i, j});
                    else if (dj > di) events.push_back({dj, j, i});
                }
            }
            // i번 소가 북쪽, j번 소가 동쪽으로 이동한다면
            // y_i <= y_j와 x_j <= x_i를 만족해야 두 소의 길이 겹친다.
            else{
                if (cows[i].y <= cows[j].y && cows[j].x <= cows[i].x){
                    int di = cows[j].y - cows[i].y;
                    int dj = cows[i].x - cows[j].x;
                    // 교차점까지의 거리가 먼 소가 멈추게 된다.
                    // 만약 거리가 같으면 멈추지 않는다.
                    if (di > dj) events.push_back({di, i, j});
                    else if (dj > di) events.push_back({dj, j, i});
                }
            }
        }

        // 두 소의 방향이 같다면
        else{
            // 두 소가 동쪽으로 이동한다면
            // 두 소의 y 좌표가 동일해야 두 소의 길이 겹친다.
            if (cows[i].d == 0){
                if (cows[i].y == cows[j].y){
                    // x 좌표가 낮은 소가 멈추게 된다.
                    if (cows[i].x < cows[j].x) events.push_back({cows[j].x - cows[i].x, i, j});
                    else if (cows[j].x < cows[i].x) events.push_back({cows[i].x - cows[j].x, j, i});
                }
            }
            // 두 소가 북쪽으로 이동한다면
            // 두 소의 x 좌표가 동일해야 두 소의 길이 겹친다.
            else{
                if (cows[i].x == cows[j].x){
                    // y 좌표가 낮은 소가 멈추게 된다.
                    if (cows[i].y < cows[j].y) events.push_back({cows[j].y - cows[i].y, i, j});
                    else if (cows[j].y < cows[i].y) events.push_back({cows[i].y - cows[j].y, j, i});
                }
            }
        }
    }

    // 이동하는 거리가 짧을수록 사건이 더 빨리 일어난다.
    // 먼저 일어나는 사건 순서대로 확인한다.
    sort(events.begin(), events.end());
    for (auto [d, i, j]: events){
        if (cows[i].dist <= d) continue; // 이미 i번 소가 멈춘 적이 있다면 넘어간다.

        // 두 소의 방향이 같다면 i번 소는 무조건 j번 소의 시작 위치에 도달하게 된다.
        if (cows[i].d == cows[j].d){
            cows[i].dist = d; // i번 소의 움직이는 거리와 끝 좌표 저장
            if (cows[i].d == 0) cows[i].ex = cows[j].x;
            else cows[i].ey = cows[j].y;
        }

        // 두 소의 방향이 다르다면
        // 멈추게끔 하는 소(j)가 멈추는 소(i)의 길에 먼저 오기 전에 다른 소에 의해 멈췄을 수 있다.
        // j번 소가 동쪽으로 움직인다면, j번 소의 x 끝 좌표가 i번 소의 x 시작 좌표를 넘어가는지 확인한다.
        else if (cows[j].d == 0){
            if (cows[i].x <= cows[j].ex){
                cows[i].dist = d; // i번 소의 움직이는 거리와 끝 좌표 저장
                cows[i].ey = cows[j].y;
            }
        }
        // j번 소가 북쪽으로 움직인다면, j번 소의 y 끝 좌표가 i번 소의 y 시작 좌표를 넘어가는지 확인한다.
        else{
            if (cows[i].y <= cows[j].ey){
                cows[i].dist = d; // i번 소의 움직이는 거리와 끝 좌표 저장
                cows[i].ex = cows[j].x;
            }
        }
    }

    for (int i = 0; i < N; i++){
        if (cows[i].dist < inf) cout << cows[i].dist << '\n';
        else cout << "Infinity\n";
    }
}

• Python

import sys; input = sys.stdin.readline
from math import inf

class Cow:
    def __init__(self, d, x, y):
        self.d = 0 if d == 'E' else 1 # 방향
        self.x = int(x) # x 시작 좌표
        self.y = int(y) # y 시작 좌표
        self.ex = inf if self.d == 0 else self.x # x 끝 좌표
        self.ey = inf if self.d == 1 else self.y # y 끝 좌표
        self.dist = inf # 움직이는 거리

N = int(input())
cows = [Cow(*input().split()) for _ in range(N)]

# 모든 소 쌍에 대해서 두 소의 길이 겹치는지 그리고 겹친다면 겹치는 점까지의 거리를 저장
events = [] # (거리, 멈추는 소의 번호, 멈추게끔 하는 소의 번호)
for i in range(N - 1):
    for j in range(i + 1, N):

        # 두 소의 방향이 다르다면
        if cows[i].d ^ cows[j].d:
            # i번 소가 동쪽, j번 소가 북쪽으로 이동한다면
            # x_i <= x_j와 y_j <= y_i를 만족해야 두 소의 길이 겹친다.
            if cows[i].d == 0:
                if cows[i].x <= cows[j].x and cows[j].y <= cows[i].y:
                    di = cows[j].x - cows[i].x
                    dj = cows[i].y - cows[j].y
                    # 교차점까지의 거리가 먼 소가 멈추게 된다.
                    # 만약 거리가 같으면 멈추지 않는다.
                    if di > dj:
                        events.append((di, i, j))
                    elif dj > di:
                        events.append((dj, j, i))
            # i번 소가 북쪽, j번 소가 동쪽으로 이동한다면
            # y_i <= y_j와 x_j <= x_i를 만족해야 두 소의 길이 겹친다.
            else:
                if cows[i].y <= cows[j].y and cows[j].x <= cows[i].x:
                    di = cows[j].y - cows[i].y
                    dj = cows[i].x - cows[j].x
                    # 교차점까지의 거리가 먼 소가 멈추게 된다.
                    # 만약 거리가 같으면 멈추지 않는다.
                    if di > dj:
                        events.append((di, i, j))
                    elif dj > di:
                        events.append((dj, j, i))

        # 두 소의 방향이 같다면
        else:
            # 두 소가 동쪽으로 이동한다면
            # 두 소의 y 좌표가 동일해야 두 소의 길이 겹친다.
            if cows[i].d == 0:
                if cows[i].y == cows[j].y:
                    # x 좌표가 낮은 소가 멈추게 된다.
                    if cows[i].x < cows[j].x:
                        events.append((cows[j].x - cows[i].x, i, j))
                    elif cows[j].x < cows[i].x:
                        events.append((cows[i].x - cows[j].x, j, i))
            # 두 소가 북쪽으로 이동한다면
            # 두 소의 x 좌표가 동일해야 두 소의 길이 겹친다.
            else:
                if cows[i].x == cows[j].x:
                    # y 좌표가 낮은 소가 멈추게 된다.
                    if cows[i].y < cows[j].y:
                        events.append((cows[j].y - cows[i].y, i, j))
                    elif cows[j].y < cows[i].y:
                        events.append((cows[i].y - cows[j].y, j, i))

# 이동하는 거리가 짧을수록 사건이 더 빨리 일어난다.
# 먼저 일어나는 사건 순서대로 확인한다.
events.sort()
for d, i, j in events:
    if cows[i].dist <= d: # 이미 i번 소가 멈춘 적이 있다면 넘어간다.
        continue

    # 두 소의 방향이 같다면 i번 소는 무조건 j번 소의 시작 위치에 도달하게 된다.
    if cows[i].d == cows[j].d:
        cows[i].dist = d # i번 소의 움직이는 거리와 끝 좌표 저장
        if cows[i].d == 0:
            cows[i].ex = cows[j].x
        else:
            cows[i].ey = cows[j].y

    # 두 소의 방향이 다르다면
    # 멈추게끔 하는 소(j)가 멈추는 소(i)의 길에 먼저 오기 전에 다른 소에 의해 멈췄을 수 있다.
    # j번 소가 동쪽으로 움직인다면, j번 소의 x 끝 좌표가 i번 소의 x 시작 좌표를 넘어가는지 확인한다.
    elif cows[j].d == 0:
        if cows[i].x <= cows[j].ex:
            cows[i].dist = d # i번 소의 움직이는 거리와 끝 좌표 저장
            cows[i].ey = cows[j].y
    # j번 소가 북쪽으로 움직인다면, j번 소의 y 끝 좌표가 i번 소의 y 시작 좌표를 넘어가는지 확인한다.
    else:
        if cows[i].y <= cows[j].ey:
            cows[i].dist = d # i번 소의 움직이는 거리와 끝 좌표 저장
            cows[i].ex = cows[j].x

for i in range(N):
    print(cows[i].dist if cows[i].dist < inf else 'Infinity')