방탈출.. 얼른 방에 들어가서 쉬고 싶다 휴 ㅠㅠ

BOJ 23743 - 방탈출 링크
(2022.09.22 기준 G2)
(치팅하면 평생 회사 탈출 못함)

문제

N개의 방과 방끼리 이을 수 있는 워프 M개가 주어지고, 각 방마다 비상탈출구를 설치할 때에 걸리는 시간 N개의 정수 ti가 주어진다면
모든 방이 출구랑 이어지게 워프나 비상탈출구를 설치하는 최소 시간 (설치는 동시에 여럿 진행할 수 없다.)

알고리즘

모든 방이 출구랑 이어지게끔 워프나 비상탈출구를 설치해야 하므로, 시간을 가중치로 생각하여 MST를 구성하면 된다.

풀이

이 문제는 언뜻 보면 되게 간단한 최소 스패닝 트리 문제 같겠지만, 난관이 하나 있다. 모든 방에 출구랑 바로 이어지는 비상탈출구를 설치할 수 있다는 점.
나는 이런 생각이 들었다. '음 그러면 모든 시간을 정렬하여 비상탈출구를 설치하는 시간이 짧은 방부터 먼저 설치하고, 이 방들을 제외하여 MST를 여럿 구성하면 되나..? 되게 복잡하겠구나..'
여기서 이런 점을 파악하였다. 비상탈출구가 몇개든 결국 워프와 비상탈출구의 개수는 동일했고 또한, 그 개수는 N개가 나온다.
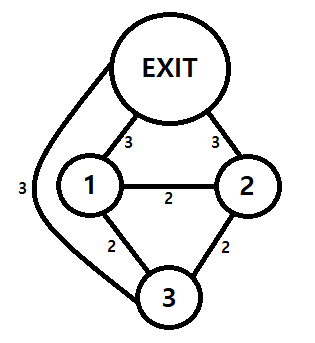
이 점에서 번뜩 생각이 났다. 결국 비상탈출구는 방과 출구를 연결하는 간선이라고 생각하고, 출구를 하나의 노드라고 생각하여 MST를 구성하면 연결된 간선의 개수는 N개가 나온다는 것을.

문제 예제 1번을 그림으로 쉽게 표현하면 이렇다.

이렇게 놓고 보면 되게 간단한 MST 문제가 된다.
방의 번호는 1번부터 시작아니깐 출구는 0번이라고 생각하면 편리할 것이다.

코드

import sys; input = sys.stdin.readline

def find(u):
    if parent[u] != u:
        parent[u] = find(parent[u])
    return parent[u]

def union(u, v):
    u = find(u)
    v = find(v)
    if u < v:
        parent[v] = u
    else:
        parent[u] = v

N, M = map(int, input().split())
edges = [list(map(int, input().split())) for _ in range(M)] # 방끼리 잇는 워프(간선)
# 출구랑 방을 잇는 비상탈출구를 간선으로 입력받는다.
for i, t in zip(range(1, N + 1), map(int, input().split())):
    edges.append([0, i, t]) # 편의상 0번을 출구라고 생각하자.

# MST 구성 시작
parent = list(range(N + 1)) # 부모 노드
ct = answer = 0 # 연결된 간선, 시간(가중치)의 합
for u, v, w in sorted(edges, key = lambda x: x[2]): # 간선들을 시간(가중치) 오름차순으로 정렬하고 차례대로 살펴보자.
    if find(u) != find(v): # 부모 노드가 다르면 union
        union(u, v)
        answer += w
        ct += 1
        if ct == N: # 만약 연결된 간선의 개수가 총 정점의 개수 - 1. 즉, N개가 되었으면 MST가 완성된 것.
            print(answer)
            break

여담

발상이 중요했던 문제다. 이런 문제를 풀어내면 뿌듯한 것 같다.