Codeforces Round 147 (Div. 2) - Build String 링크
(2023.08.09 기준 Difficulty *2000)

문제

문자열 t와 문자열 s1, s2, ..., sn이 주어진다.

문자열 t를 만들어야 하는데, 각 문자를 s1, s2, ..., sn 중 선택하여 동일한 문자를 가져와야 한다.
이 때, 문자는 한번만 가져갈 수 있으며 가져가는 비용은 i가 들어간다. 즉, s1, s2, ..., sn에서 하나의 문자를 가져가는 비용은 1, 2, ..., n이 든다.
그리고 s1, s2, ..., sn에서 문자를 들고갈 수 있는 횟수 a1, a2, ..., an이 주어진다.

문자열 t를 만들기 위한 최소 비용 출력

알고리즘

전형적인 MCMF

풀이

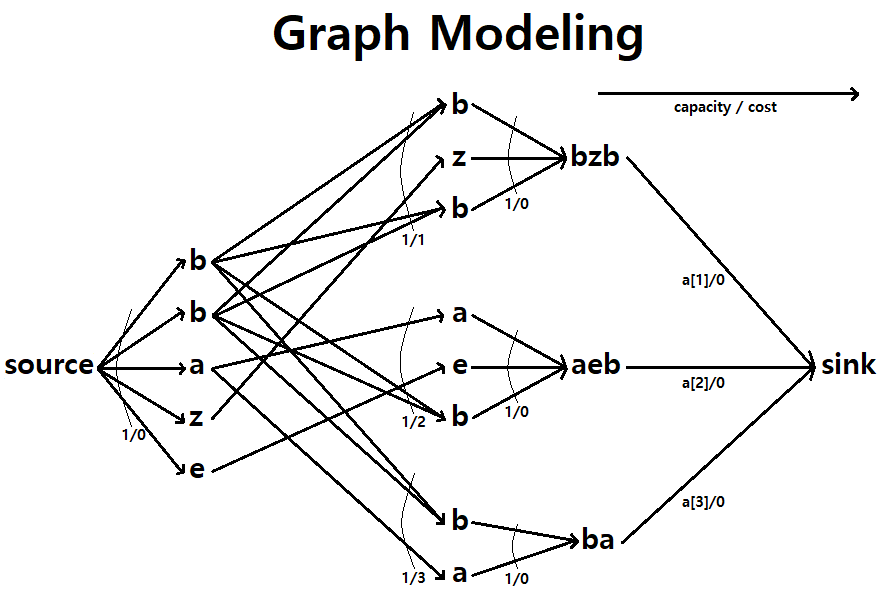
문자열 t의 각 문자가 하나씩 사용되어야 하므로 source -> t의 각 문자로 간선을 잇고 용량은 1

t의 각 문자는 si의 문자열의 문자를 하나 꺼내써야 하는데, 이때 비용은 i(1-based index)이므로 t의 각 문자 -> si의 각 문자로 일치하는 문자끼리 간선을 잇고 용량은 1, 비용은 i

si는 각 사용할 수 있는 횟수 ai가 있으므로 si의 각 문자 -> si로 간선을 잇고 용량은 1. si -> sink로 간선을 잇고 용량은 ai

그래프 모델링을 첫번째 예시로 하여금 그림으로 나타내면 다음과 같다.

코드

• C++

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 111, MAXL = 11111, inf = INT_MAX;

int N, n, A[MAXN], M[MAXN], s, t, source, sink;
string T, S[MAXN];

struct Edge{
    int v, w, c, p;

    Edge(int v, int w, int c, int p): v(v), w(w), c(c), p(p){};
};

struct Zkw{
    int source, sink, length, ei, pointer[MAXL], distance[MAXL], work[MAXL];
    bool visited[MAXL];
    vector<Edge> edges;

    void init();

    void add_edge(int u, int v, int w, int c){ // 단방향
        edges.push_back({v, w, c, pointer[u]});
        pointer[u] = ei++;
        edges.push_back({u, 0, -c, pointer[v]});
        pointer[v] = ei++;
    }

    void _spfa(){
        deque<int> dq; dq.push_back(source);
        bool in_q[length]; fill(in_q, in_q + length, false); in_q[source] = true;
        distance[source] = 0;
        while (!dq.empty()){
            int here = dq.front(); dq.pop_front();
            in_q[here] = false;
            for (int p = pointer[here]; ~p; p = edges[p].p)
                if (edges[p].w && distance[edges[p].v] > distance[here] + edges[p].c){
                    distance[edges[p].v] = distance[here] + edges[p].c;
                    if (!in_q[edges[p].v]){
                        dq.push_back(edges[p].v);
                        in_q[edges[p].v] = true;
                    }
                }
        }
    }

    int _dfs(int here, int f){
        visited[here] = true;
        if (here == sink) return f;
        for (int p = work[here]; ~p; p = work[here] = edges[p].p)
            if (!visited[edges[p].v] && edges[p].w && distance[edges[p].v] == distance[here] + edges[p].c){
                int result = _dfs(edges[p].v, min(f, edges[p].w));
                if (result){
                    edges[p].w -= result;
                    edges[p ^ 1].w += result;
                    return result;
                }
            }
        return 0;
    }

    bool _update(){
        int d = inf;
        for (int here = 0; here < length; here++) if (visited[here])
            for (int p = pointer[here]; ~p; p = edges[p].p)
                if (!visited[edges[p].v] && edges[p].w)
                    d = min(d, distance[here] - distance[edges[p].v] + edges[p].c);
        if (d < inf){
            for (int here = 0; here < length; here++) if (!visited[here]) distance[here] += d;
            return true;
        }
        return false;
    }

    void run(){
        fill(distance, distance + length, inf);
        _spfa();

        int F = 0, C = 0;
        while (true){
            for (int i = 0; i < length; i++) work[i] = pointer[i];
            while (true){
                fill(visited, visited + length, false);
                int f = _dfs(source, inf);
                if (!f) break;
                F += f;
                C += distance[sink] * f;
            }
            if (!_update()) break;
        }
        cout << (F == n ? C : -1);
    }
}zkw;

void Zkw::init(){
    length = sink + 1;

    ei = 0;
    fill(pointer, pointer + length, -1);
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    cin >> T >> N; n = T.size();

    fill(M, M + N + 1, 0);
    for (int i = 0; i < N; i++){
        cin >> S[i] >> A[i];
        M[i + 1] = M[i] + S[i].size() + 1; // s[i]의 각 글자와 s[i]는 [m[i], m[i+1])에 매칭된다.
    }

    // S : [0, M[N]]), T : [M[N], M[N] + n), source : M[N] + n, sink : M[N] + n + 1
    s = 0; t = M[N]; zkw.source = source = M[N] + n; zkw.sink = sink = source + 1;
    zkw.init();

    // source -> T -> S의 각 글자 -> S -> sink
    
    // source -> T
    for (int i = 0; i < n; i++) zkw.add_edge(source, i + t, 1, 0);
    
    // T -> S의 각 글자
    for (int i = 0; i < n; i++) for (int j = 0; j < N; j++) for (int k = 0, sz = S[j].size(); k < sz; k++)
        if (T[i] == S[j][k]) zkw.add_edge(i + t, M[j] + k + s, 1, j + 1);
    
    // S의 각 글자 -> S
    for (int i = 0; i < N; i++) for (int j = 0, sz = S[i].size(); j < sz; j++)
        zkw.add_edge(M[i] + j + s, M[i + 1] - 1 + s, 1, 0);
    
    // S -> sink
    for (int i = 0; i < N; i++) zkw.add_edge(M[i + 1] - 1 + s, sink, A[i], 0);

    zkw.run();
}

• Python (PyPy3)

import sys; input = sys.stdin.readline
from math import inf
from collections import deque

class Edge:
    def __init__(self, v, w, c, p):
        self.v = v # u - v
        self.w = w # capacity
        self.c = c # cost
        self.p = p # pointer

class Zkw:
    def __init__(self):
        self.source = source
        self.sink = sink
        self.length = self.sink + 1

        self.ei = 0
        self.edges = []
        self.pointer = [-1] * self.length

    def add_edge(self, u, v, w, c): # 단방향
        self.edges.append(Edge(v, w, c, self.pointer[u]))
        self.pointer[u] = self.ei
        self.edges.append(Edge(u, 0, -c, self.pointer[v]))
        self.pointer[v] = self.ei + 1
        self.ei += 2

    def _spfa(self):
        dq = deque([self.source])
        in_q = [False] * self.length; in_q[self.source] = True
        self.distance[self.source] = 0
        while dq:
            here = dq.popleft()
            in_q[here] = False
            p = self.pointer[here]
            while ~p:
                if self.edges[p].w and self.distance[self.edges[p].v] > self.distance[here] + self.edges[p].c:
                    self.distance[self.edges[p].v] = self.distance[here] + self.edges[p].c
                    if not in_q[self.edges[p].v]:
                        dq.append(self.edges[p].v)
                        in_q[self.edges[p].v] = True
                p = self.edges[p].p

    def _dfs(self, here, f):
        self.visited[here] = True
        if here == self.sink:
            return f
        p = self.work[here]
        while ~p:
            if not self.visited[self.edges[p].v] and self.edges[p].w and self.distance[self.edges[p].v] == self.distance[here] + self.edges[p].c:
                result = self._dfs(self.edges[p].v, min(f, self.edges[p].w))
                if result:
                    self.edges[p].w -= result
                    self.edges[p ^ 1].w += result
                    return result
            p = self.work[here] = self.edges[p].p
        return 0

    def _update(self):
        d = inf
        for here in range(self.length):
            if self.visited[here]:
                p = self.pointer[here]
                while ~p:
                    if not self.visited[self.edges[p].v] and self.edges[p].w:
                        d = min(d, self.distance[here] - self.distance[self.edges[p].v] + self.edges[p].c)
                    p = self.edges[p].p
        if d < inf:
            for here in range(self.length):
                if not self.visited[here]:
                    self.distance[here] += d
            return True
        return False

    def run(self):
        self.distance = [inf] * self.length
        self._spfa()

        F = C = 0
        while True:
            self.work = [self.pointer[i] for i in range(self.length)]
            while True:
                self.visited = [False] * self.length
                f = self._dfs(self.source, inf)
                if not f:
                    break
                F += f
                C += self.distance[self.sink] * f
            if not self._update():
                break
        print(C) if F == n else print(-1)

T = input().strip(); n = len(T)
N = int(input())

S = []; A = []; M = [0] * (N + 1)
for i in range(N):
    s, a = input().split()
    S.append(s)
    A.append(int(a))
    M[i + 1] = M[i] + len(s) + 1 # s[i]의 각 글자와 s[i]는 [m[i], m[i+1])에 매칭된다.

# S : [0, M[N]]), T : [M[N], M[N] + n), source : M[N] + n, sink : M[N] + n + 1
s = 0; t = M[N]; source = M[N] + n; sink = source + 1
zkw = Zkw()

# source -> T -> S의 각 글자 -> S -> sink

# source -> T
for i in range(n):
    zkw.add_edge(source, i + t, 1, 0)

# T -> S의 각 글자
for i in range(n):
    for j in range(N):
        for k in range(len(S[j])):
            if T[i] == S[j][k]:
                zkw.add_edge(i + t, M[j] + k + s, 1, j + 1)

# S의 각 글자 -> S
for i in range(N):
    for j in range(len(S[i])):
        zkw.add_edge(M[i] + j + s, M[i + 1] - 1 + s, 1, 0)

# S -> sink
for i in range(N):
    zkw.add_edge(M[i + 1] - 1 + s, sink, A[i], 0)

zkw.run()