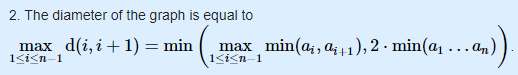Codeforces Round #813 (Div. 2) - Empty Graph 링크
(2022.10.20 기준 Difficulty *2000)
(Never cheat)

문제

크기가 n인 배열 a와 양수 k가 주어지고, ai = x 작업을 최대 k번할 수 있다.
간선 (l, r)의 가중치는 min(al, al+1, ..., ar-1, ar)이고
그래프의 직경은 모든 두 정점 쌍의 가중치의 최대다.
최대 k번 작업 후에 가능한 최대 그래프의 직경을 출력

알고리즘

그리디도 가능하다. 하지만 이분 탐색을 이용하여 배열에 작업을 직접 하면서 구하는게 훨씬 쉬운 것 같다.

풀이

솔직히 아직 정확하게 이해를 못했다. 일단 문제의 공식 풀이를 참고하여 적어보겠다.
공식 풀이

그래프의 직경은 min(max(min(ai, ai+1)) (1 <= i < n), 2 * min(a1, ..., an)) 이라고 한다.
우리는 그래프의 직경을 임의로 정해서 조정할 것이다. 이분 탐색으로.

일단 min(a)*2가 직경보다 같거나 커야 한다. 즉, 직경/2보다 작은 a의 원소는 전부 교체 작업을 해야 하는 것이다. 이 때, 작업 수를 세자.

작업 수가 k보다 크면 이 직경은 불가능한 것이다. 그러므로 범위를 낮추자.

작업 수가 k와 같다면 max(min(ai, ai+1)) 식을 만족해야 한다.
그러므로 a1부터 an까지 인접 원소끼리 min 연산을 하여 나오는 최댓값을 직경이랑 비교를 하여
max보다 직경이 크다면 불가능한 것이므로 범위를 낮추자.
max보다 직경이 같거나 작으면 가능한 것이므로 출력할 답에 직경을 저장한 다음 범위를 높이자.

작업 수가 k - 1이라면 작업 수가 한 번 남는 것이다.
그러면 작업을 max(a)의 인근에 해야 max(min(ai, ai+1)) 연산으로 인해 직경이 커진다.
즉, max(a)가 직경보다 같거나 커야 인근에 작업을 취하여 그 직경을 넘길 수 있는 것이다.

작업 수가 k - 2라면 아무 두 원소나 10**9까지 교체해버리면 직경이 올라가는 것이므로 무조건 가능한 것이다.

위와 같은 임의로 정한 직경에 따라 어떻게 할지 분기가 나뉘고, 분기마다 직경을 조정해나가면서 가능한 최대 직경을 이분 탐색으로 찾아나가는 것이다.

코드

import sys; input = sys.stdin.readline
 
def solve():
    n, k = map(int, input().split())
    a = list(map(int, input().split()))
 
    # 이분 탐색
    start = 0; end = 1000000000
    result = 0
    while start <= end:
        mid = (start + end) // 2
        arr = a[:] # 배열 복사
        K = k # 남은 작업 수
 
        # 임의로 정한 직경에 따라 배열을 조작
        # 남은 작업 수에 따라 분기가 나뉜다.
 
        # mid = min(max(min(ai, ai+1)) (1 <= i < n), 2 * min(a1, ..., an))
        # 2 * min(a1, ..., an) 부터 만족시켜보자.
        for i in range(n):
            if arr[i] < mid / 2: # mid / 2보다 작으면 1000000000으로 교체 작업
                arr[i] = 1000000000
                K -= 1
 
        # 남은 작업 수가 음수이면 이 mid는 불가능한 직경이다.
        if K < 0:
            end = mid - 1
 
        # 남은 작업 수가 0이면 max(min(ai, ai+1)) (1 <= i < n)을 계산하여 비교
        elif not K:
            MAX = 0
            for i in range(n - 1):
                MAX = max(MAX, min(arr[i], arr[i + 1]))
            if MAX < mid: # max보다 mid가 크면 불가능한 직경이다.
                end = mid - 1
            else: # max보다 mid가 같거나 작으면 가능한 직경이다.
                result = mid
                start = mid + 1
 
        # 남은 작업 수가 1이면
        # 최대한 mid가 직경이 될 수 있도록
        # arr의 최댓값 인근에 작업을 해야 한다.
        elif K == 1:
            if max(arr) < mid: # 최댓값보다 mid가 크면 불가능한 직경이다.
                end = mid - 1
            else: # 최댓값보다 mid가 같거나 작으면 가능힌 직경이다.
                result = mid
                start = mid + 1
 
        # 남은 작업 수가 2 이상이면
        # 인접한 아무 두 원소를 최대로 올려버리면 무조건 mid는 가능한 직경이다.
        else:
            result = mid
            start = mid + 1
 
    print(result)
 
for _ in range(int(input())):
    solve()