본 게시물은 코드프레소의 code.PRESS-UP 체험단 과정을 담은 게시물입니다.

해당 게시물 수강강좌 :

파이썬으로 시작하는 통계 데이터 분석

파이썬 라이브러리를 사용하여 통계 데이터 분석 시작하기

https://www.codepresso.kr/course/57

이번 포스팅은 지난 포스팅에 이어서 데이터 전처리 Part2 입니다.
결측값과 이상값을 어떻게 처리하는지 자세하게 알아보도록 하겠습니다.

코드프레소 강의와 함께 들여다 보도록 하겠습니다.

1. 데이터 결측값 처리

❔ 결측값이란 입력이 누락된 값을 의미
❔ 결측값은 NA, 999999, NULL 등으로 표현함

1-1. 데이터 결측값의 종류

📊 1. 완전 무작위 결측(Missing Completely At Random)

• 변수상에서 발생한 결측값이 다른 변수들과 아무런 상관이 없는 경우
• 다른 관측값의 결측으로인해 영향 받지 않고 결측값이 발생

📊 2. 무작위 결측(Missing At Random)

• 누락된 자료가 특정 변수와 관련되어 일어나지만, 그 변수의 결과는 관계가 없는 경우
• 누락이 전체 정보가 있는 변수로 설명이 될 수 있음을 의미
• 다른 변수들을 이용해 예측이 가능함

📊 3. 비 무작위 결측(Missing Not At Random)

• 누락된 값이 다른 변수와 연관이 있는 경우
• 무작위 결측에서 다른 변수들을 이용해 예측이 불가능한 결측값인 경우
• 무시할 수 없는(non - ignorable) 결측값

결측값 대체 조건 : 결측값의 종류가 완전 무작위 결측/무작위 결측 임을 가정하고 삭제하거나 대체하는 것

1-2. 데이터 결측값 처리 절차

Ⅰ. 결측값 식별

• 원본 데이터에서 다양한 형태로 결측 정보가 표현되어 있으므로 현황 파악을 해야함

Ⅱ. 결측값 부호화

• 파악된 정보를 바탕으로 컴퓨터가 처리 가능한 형태로 부호화
• NA(Not Available), NaN(Not a Number), inf(Infinite), NULL, 999, etc...

Ⅲ. 결측값 대체

• 결측값을 자료형에 맞춰 대체 알고리즘을 통해 결측값을 처리

1-3. 데이터 결측값 처리 방법

🏸 단순 대치법

• 결측값을 그럴듯한 값으로 대체하는 통계적 기법
• 결측값을 가진 자료 분석에 사용하기가 쉽고, 통계적 추론에 사용된 통계량의 효율성 및 일치성 등의 문제를 부분적으로 보완
• 대체된 자료는 결측값 없이 완전한 형태를 지님

단순대치법 종류

완전 분석법

• 불완전 자료는 모두 무시하고 완전하게 관측된 자료만 사용하여 분석하는 방법
• 분석은 쉽지만 부분적으로 관측된 자료가 무시되어 효율성이 상실되고 통계적 추론의 타당성 문제가 발생

평균 대치법

• 관측 또는 실험되어 얻어진 자료의 평균값으로 결측값을 대치해서 불완전한 자료를 완전한 자료로 만드는 방법
• 대표적 방법으로 관측값이 빠져있을 경우 평균으로 대치하는 비 조건부 평균 대치법과 회귀분석을 활용하여 결측값을 대치하는 조건부 평균 대치법이 있음

단순 확률 대치법

• 평균 대치법에서 관측된 자료를 토대로 추정된 통계량으로 결측값을 대치할 때 어떤 적절한 확률값을 부여한 후 대치하는 방법
• 무응답을 현재 진행 중인 연구에서 비슷한 성향을 가진 응답자의 자료로 대체하는 핫덱(Hot-Deck) 대체, 핫덱과 비슷하나 대체할 자료를 현재 진행 중인 연구에서 얻는 것이 아닌 외부 출처 또는 이전의 비슷한 연구에서 가져오는 콜드덱(Cold-Deck) 대체, 몇가지 다른 방법을 혼합하는 혼합 방법이 있음

🏸 다중 대치법

• 단순 대치법을 한 번 하지 않고 m번 대치를 통해 m 개의 가상적 완전한 자료를 만들어서 분석하는 방법
• 원 표본의 결측값을 한 번 이상 대치하여 여러 개의 대치된 표본을 만들어야 하므로 항상 같은 값으로 결측 자료를 대치할 수 없음
• 여러 번의 대체표본으로 대체 내 분산과 대체 간 분산을 구하여 추정치의 총 분산을 추정하는 방법
• 대체로 발생하는 불확실성은 대체-간 부분에서 고려함으로써 과소 추정된 분산 추정치가 원 분산에 가까워지도록 해야 함
• 다중 대치법은 대치 -> 분석 -> 결합의 3단계의 구성

대치

• 각 대치표본은 결측 자료의 예측분포 또는 사후분포(Posterior Distribution)에서 추출된 값으로 결측값을 대치하는 방법 활용
• 다중 대치 방법은 베이지안 방법(Bayes' Theorem) 이용

  베이지안 방법
  어떤 사건의 관측 전의 원인에 대한 가능성과 관측 후 원인의 가능성 사이의 관계를 설명하는 확률이론

분석

• 같은 예측 분포로부터대치 값을 구하여 D개의 대치표본을 구하게 되면 이 D개의 대치표본으로부터 원하는 분석을 각각 수행

결합

• 모수의 점 추정(Point Estimation)과 표준 오차의 추정치를 D개 구한 후 이들을 결합하여 하나의 결과를 제시

  점 추정
  통게학에서 미지의 분포에 대하여 가장 근사한 단일값을 구하는 기법을 말함

2. 데이터 이상값 처리

❔ 데이터 이상값은 관측된 데이터의 범위에서 많이 벗어난 아주 작은 값이나 아주 큰 값을 의미
❔ 데이터 이상값은 입력 오류, 데이터 처리 오류 등의 이유로 특정 범위에서 벗어난 데이터 값을 의미

2-1. 데이터 이상값 발생 원인

1. 데이터 입력 오류

• 데이터를 수집하는 과정에서 발생할 수 있는 에러
• 전체 데이터의 분포를 보면 쉽게 발견 가능

2. 측정오류

• 데이터를 측정하는 과정에서 발생하는 에러

3. 실험오류

• 실험조건이 동일하지 않은 경우 발생

4. 고의적인 이상값

• 자기 보고식 측정에서 나타나는 에러
• 정확하게 기입한 값이 이상값으로 보일 수 있음

5. 표본추출 에러

• 데이터를 샘플링하는 과정에서 나타나는 에러

2-2. 데이터 이상값 검출 방법

1. 개별 데이터 관찰

• 전체 데이터의 추이나 특이 사항을 관찰하여 이상값 검출
• 전체 데이터 중 무작위 표본 추출 후 관찰하여 이상값 추출

2. 통계 기법(값) 이용

• 통계 지표 데이터(평균, 중앙값, 최빈값)와 데이터 분산도(범위, 분산)를 활용한 이상값 검출

  검출기법

  🏸 ESD
  평균으로 부터 3 표준편차 떨어진 값(0.15%)을 이상값으로 판단

  🏸 기하평균 활용
  기하평균으로부터 2.5 표준편차 떨어진 값을 이상값으로 판단
  ❔ 기하평균 : n개의 양수 값을 모두 곱한 것의 n제곱근

  🏸 사분위 수 활용
  제1사분위, 제3사분위를 기준으로 사분위간 범위의 1.5배 이상 떨어진 값을 이상값으로 판단

  🏸 표준화 점수(Z-score) 활용
  정규분포를 따르는 관측치들이 자료의 중심인평균에서 얼마나 떨어져 있는지를 나타냄에 따라서 이상값을 검출

  🏸 딕슨의 Q-검정
  오름차순으로 정렬된 데이터에서 범위에 대한 관측치 간의 차이의 비율을 활용하여 이상값 여부를 검정하는 방법

  🏸 그럽스의 T-검정
  정규 분포를 만족하는 단변량 자료에서 이상값을 검정하는 방법

  🏸 카이제곱 검정
  데이터가 정규 분포를 만족하나, 자료의 수가 적은 경우에 이상값을 검정하는 방법

3.시각화 이용

• 데이터 시각화(Data Visualization)를 통한 지표 확인으로 이상값 검출
• 확률 밀도 함수, 히스토그램, 시계열 차트 등

4. 머신 러닝 기법 이용

• 데이터 군집화를 통한 이상값 검출
• 주어진 데이터를 K개의 클러스터로 묶고, 각 클러스터와 거리 차이의 분산을 최소화 하는 방식의 K-평균 군집화 알고리즘 등이 있음

5. 마할라노비스 거리(Mahalanobis Distance) 활용

• 데이터의 분포를 고려한 거리 측도로, 관측치가 평균으로부터 벗어난 정도를 측정하는 통계량 기법
• 데이터의 분포를 측정할 수 있는 마할라노비스 거리를 이용하여 평균으로부터 벗어난 이상값을 검출할 수 있음
• 이상값 탐색을 위해 고려되는 모든 변수 간에 성형관계를 만족하고, 각 변수들이 정규분포를 따르는 경우에 적용할 수 있는 전통적인 접근법

6.LOF(Local Outlier Factor)

• 관측지 주변의 밀도와근접한 관측치 주변 밀도의 상대적인 비교를통해 이상값을 탐색하는 기법
• 각 관측치에서 K번째 근접이웃까지의 거리를 산출하여 해당 거리 안에 포함되는 관측치의 개수를 나눈 역수 값으로 산출

7.iForest(Isolation Forest)

• 관측치 사이의 거리 또는 밀도에 의존하지 않고, 데이터 마이닝 기법인 의사결정나무를 이용하여 이상값을 탐지하는 방법
• 의사결정나무 기법으로 분류 모형을 생성하여 모든 관측치를 고립시켜나가면서 분할 횟수로 이상값을 탐색
• 데이터의 평균적인 관측치와 멀리 떨어진 관측치일수록 적은 횟수의 공간 분할을 통해 고립시킬 수 있음
• 의사결정나무 모형에서 적은 횟수로 리프 노트에 도달하는 관측치일수록 이상값일 가능성이 큼

3. 데이터 이상값 처리

3-1. 삭제

🏸 이상값으로 판단되는 관측값을 제외하고 분석하는 방법
🏸 추정치의 분산은 작아지지만 실제보다 과소 또는 과대 추정되어 편의가 발생할 가능성이 있음
🏸 이상값을 제외시키기 위해 양극단의 값을 절단하기도 함
🏸 절단을 위해 기하평균 혹은 하단, 상단 %를 이용함
🏸 이상값 자료도실제 조사된 수치이므로 이상값을 제외하는 것은 현실을 제대로 반영하는 방법으로 적절하지 않을 수도 있음
🏸 극단값 절단 방법을 활용해 데이터를 제거하는 것 보다는 극단값 조정 방법을 활용하는 것이 데이터 손실률이 적고, 설명력이 높아짐

3-2. 대체

🏸 하한값과 상한값을 결정한 후 하한값보다 작으면 하한값으로 대체, 상한값보다 크면 상한값으로 대체
🏸 이상값을 평균이나 중앙값 등으로 대체하는 방법
🏸 데이터의 결측값 처리의 내용과 동일

3-3. 변환

🏸 극단적인 값으로 인해 이상값이 발생했다면 자연로그를 취해서 값을 감소시킬 수 있음
🏸 상한값과 하한값을 벗어나는 값들을 하한, 상한값으로 바꾸어 활용하는 극단값 조정 방법도 활용됨

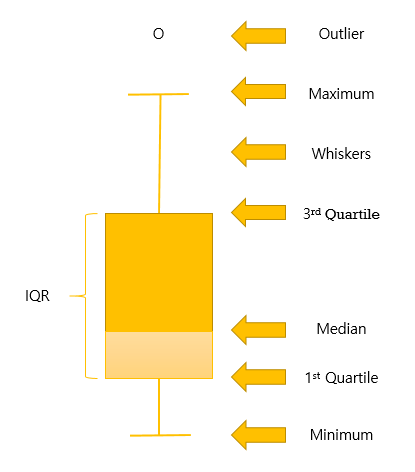
3-4. 박스플롯 해석을 통한 이상값 제거

🏸 사분위 수를 이용해서 제거하는 방법을 사용
🏸 이상값을 구하기 위해서는 수염을 이용하게 되고, 수염 밖에 있는 값을 이상값으로 판단

3-5. 분류하여 처리

• 이상값이 많을 경우에 사용하는 방법
• 서로 다른 그룹으로 통계적인 분석을 실행하여 처리
• 각각의 그룹에 대해서 통계적인 모형을 생성하고, 결과를 결합하는 방법을 사용함

이번 포스팅역시 내용이 많습니다.
통계학은 포스팅 한두개로 정리되는 학문이 아닙니다.

다음 포스팅역시 통계학과 관련된 포스팅입니다.
코드프레소 강의 내용 시 쉽지 않네요