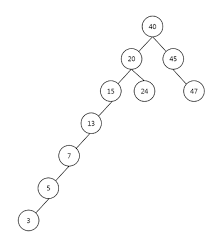
AVL Tree 🌲
간단하게 말해서 이진 탐색 트리의 단점을 극복할 수 있는 자료구조이다. 왜 이름이 AVL이냐면 발명자의 이름인 Adelson-Velsky and Landis에서 따와서 그렇다.
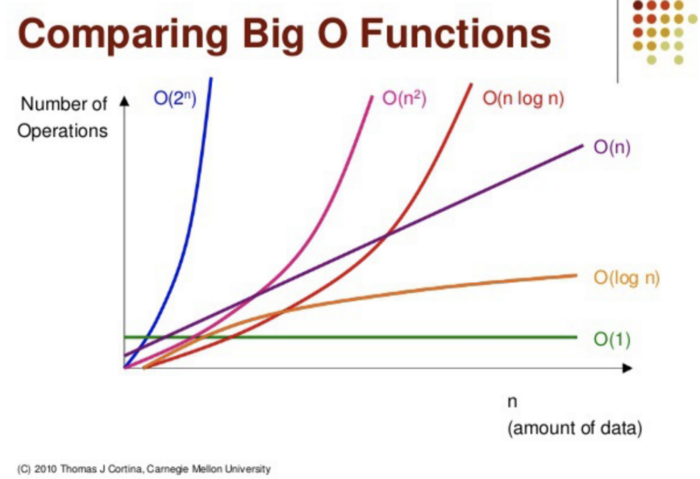
위 그림은 여러 시간 복잡도를 알기 쉽게 그래프로 나타낸 것이다. O(1)이 가장 빠르고 위로 갈수록 느린 결과를 보인다. 앞서 말한 것 처럼 이진 탐색 트리는 문제점을 가지는데 아래 그림과 같이 설명하고자 한다.
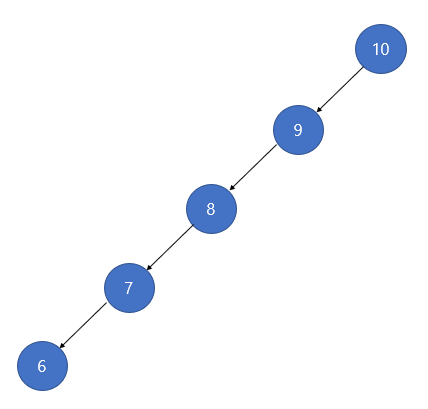
그냥 이진 탐색 트리는 그림과 같이 한쪽으로 노드가 취우치는 상황이 생길 수 있다. 이런 상황에서 특정 값을 찾아야 할때는 O(N)의 시간이 걸릴 수도 있다. 그리하여 한 특정 값을 찾아내려면 트리 전체를 탐색해야 나올 수가 있는 단점이 있다. 이를 간단하게 말하면 다음과 같다.
한쪽으로 치우친 편향 이진트리가 되면 트리의 높이가 높아지기 때문에 이를 방지하고자 높이 균형을 유지하는 AVL 트리를 사용한다.
AVL 트리는 다른 말로자가 균형 이진 탐색 트리라 한다.
또 다른 그림을 들고 와보면
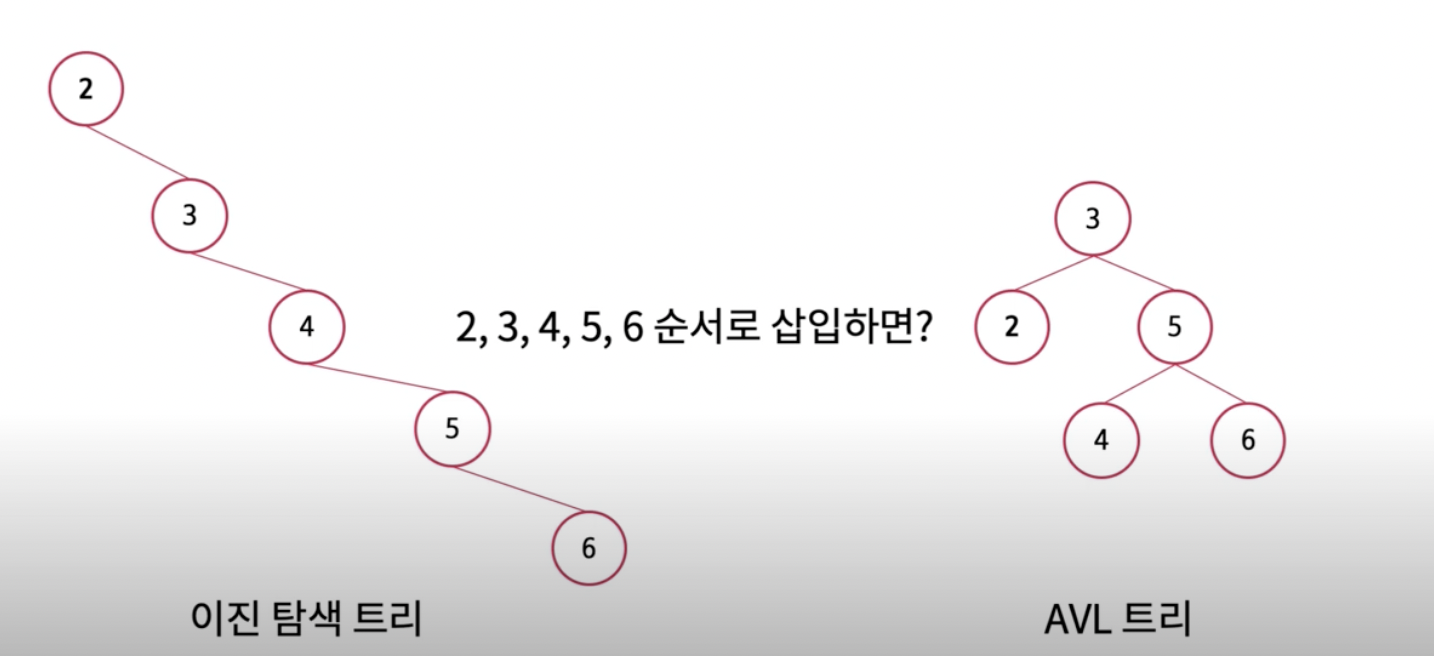
딱 봐도 트리가 한쪽으로 몰려있는 것을 알 수 있다. 이럴때 균형을 잡아주는 게 AVL 트리다.
AVL 트리의 정의 및 특징은?
스스로 균형을 잡는 데이터 구조 중 처음으로 발명되었다. AVL 트리에서, 두 자식 서브트리의 높이는 항상 최대 1만큼 차이난다. 만약 어떤 시점에서 높이 차이가 1보다 커지면 이 속성을 유지하기 위해서 스스로 균형을 잡는다.
높이차이는 뭐고 뭔소린가 싶었다. 다시 말을 풀이해보자. 먼저 균형을 잡는다고 했는데 이를 어떻게 잡을 수 있는 것일까?
-
AVL Tree의 특징.
🌲 - 이진 트리의 속성을 가진다.
🌲 - 왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1이다.
🌲 - 어떤 시점에서 높이 차이가 1보다 커지면 회전(rotation)을 통해 균형을 잡아 차이를 줄인다.
🌲 - AVL 트리는 높이를 logN으로 유지하기 떄문에 삽입, 검색, 삭제의 시간 복잡도는 O(logN)이다.
균형(밸런스) 잡는 방법! 🛹

- Balance Factor
라는 것을 사용한다. 이는 왼쪽과 오른쪽의 자식(노드)의 높이 차이를 뜻하는 말이다.
Balance Factor는 균형인수라고도 표현한다. 이 균형 인수의 절대 값이 클 수록 트리의 균형이 무너진 것이다. 먼저 높이를 계산해보자.
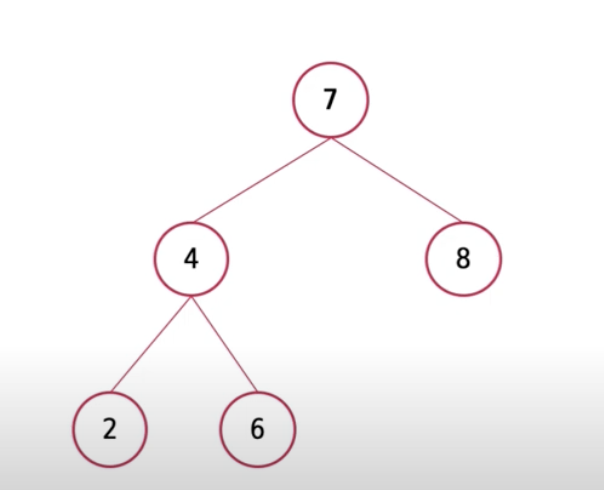
높이는 가장 아래에서부터 올라가 계산한다. Leaf 노드의 높이는 항상 0이며 둘중 가장 큰값인 노드의 높이로 계산된다. 그리고 맨 위쪽으로 다시 올라가 4번 자식 노드와 8번 자식노드중 가장 큰값으로 높이가 계산된다.
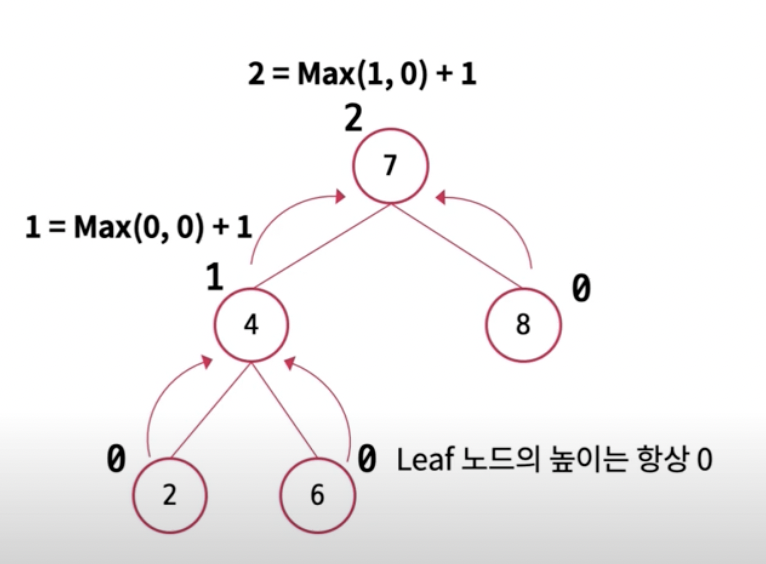
부모 노드 높이 = Max(좌측 노드 높이, 우측 노드 높이) + 1
만약에 다른 예시로 자식이 없는 노드가 있다면? 즉, NULL인 경우 높이를 -1로 본다. 그 후 모든 Leaf노드 들은 높이가 0이 되고 가장 깊은 노드부터 위쪽으로 계산해서 올라간다.
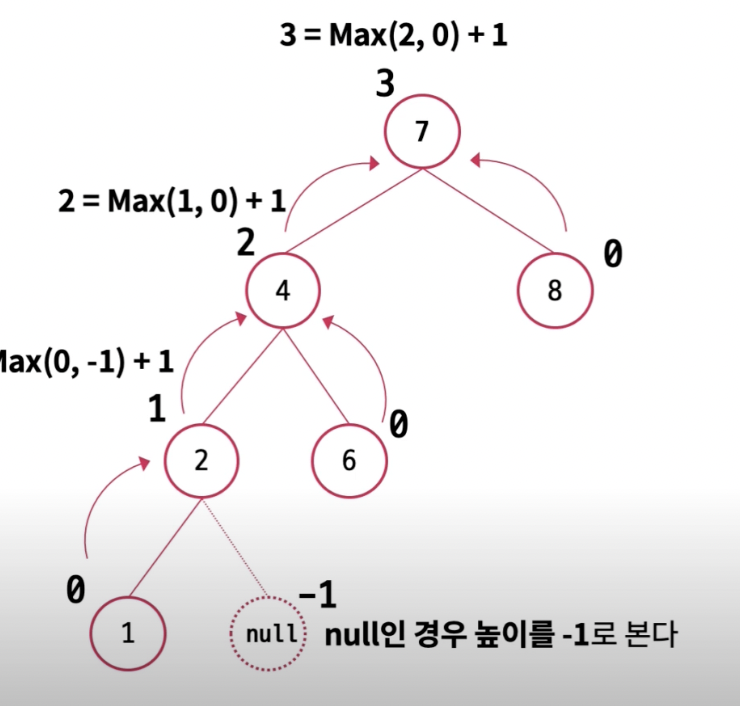
2번 노드의 높이는 1이 되고 4번 노드는 1+1, 맨 마지막 7번 노드의 높이는 3이 된다. 높이를 알고 있다면 균형도를 계산할 수 있다. 위에서 말했다 시피 균형도는 좌측 노드 높이 - 우측 노드 높이 이다. 균형도도 마찬가지로 아래에서 부터 올라가 계산된다. 계산된 균형도가 양수라면 좌측, 음수라면 우측으로 비대한 트리임을 알 수 있다.
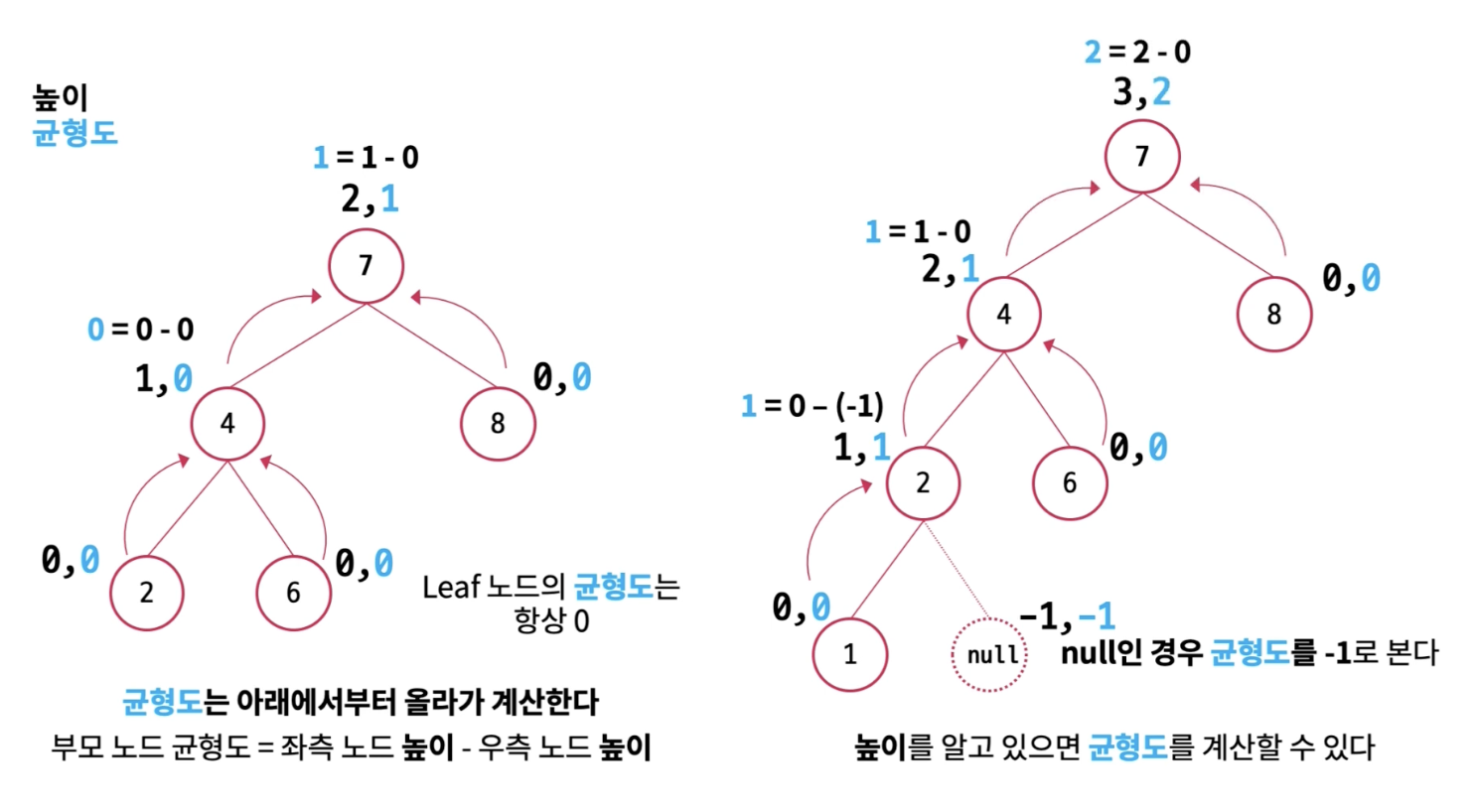
트리 불균형 문제.
이는 4 가지로 나뉜다.
- LL problem : Left - Left로 서브 트리가 비대해지는것.
- LR problem : Left - Right로 서브 트리가 비대해지는것.
- RR problem : Right - Right로 서브 트리가 비대해지는것.
- RL problem : Right - Lefe로 서브 트리가 비대해지는것.
🌲 LL 문제.
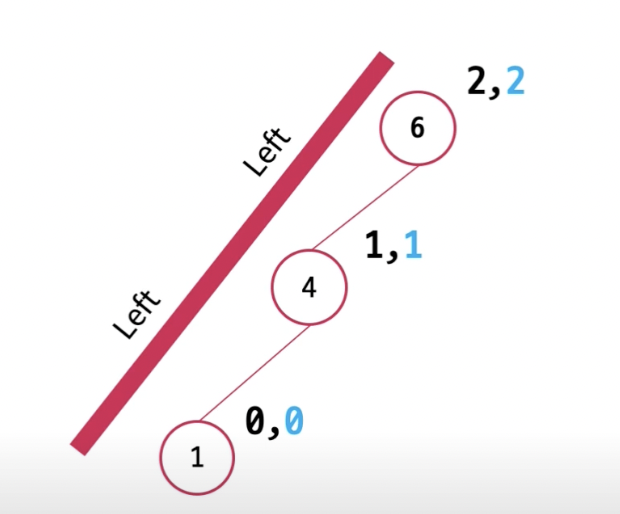
🌲 RR 문제.
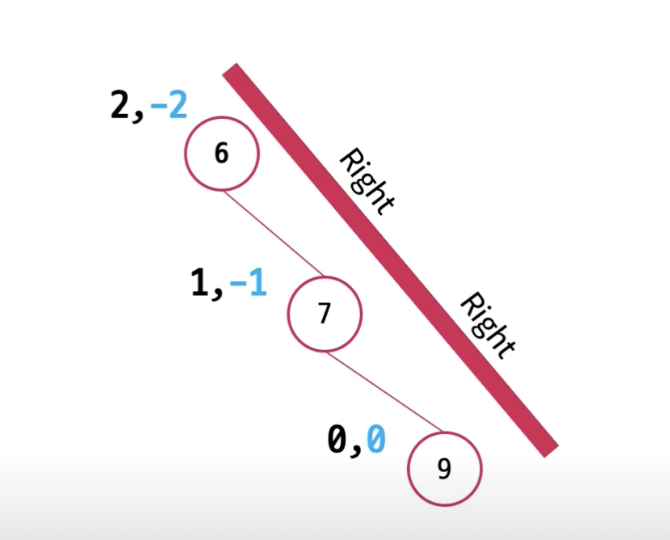
🌲 LR 문제.

🌲 RL 문제.
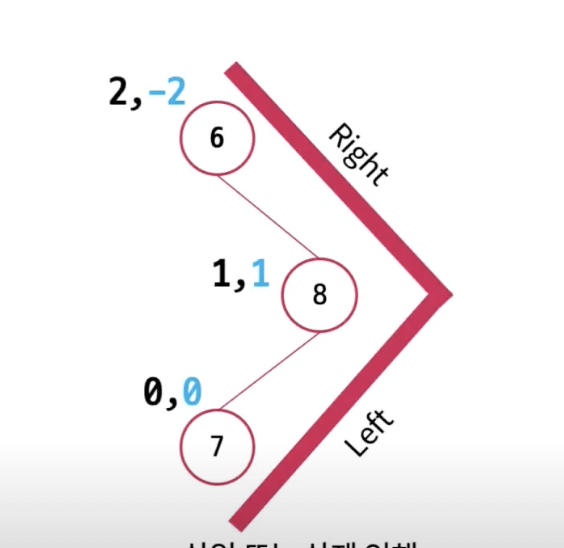
회전(rotation) 🔄
위에 이 4가지 문제들을 해결하기 위해선 회전(rotation)을 해서 균형도를 2미만으로 맞춰야 한다. 회전을 막 할 수는 없는데 어찌하면 좋을까?
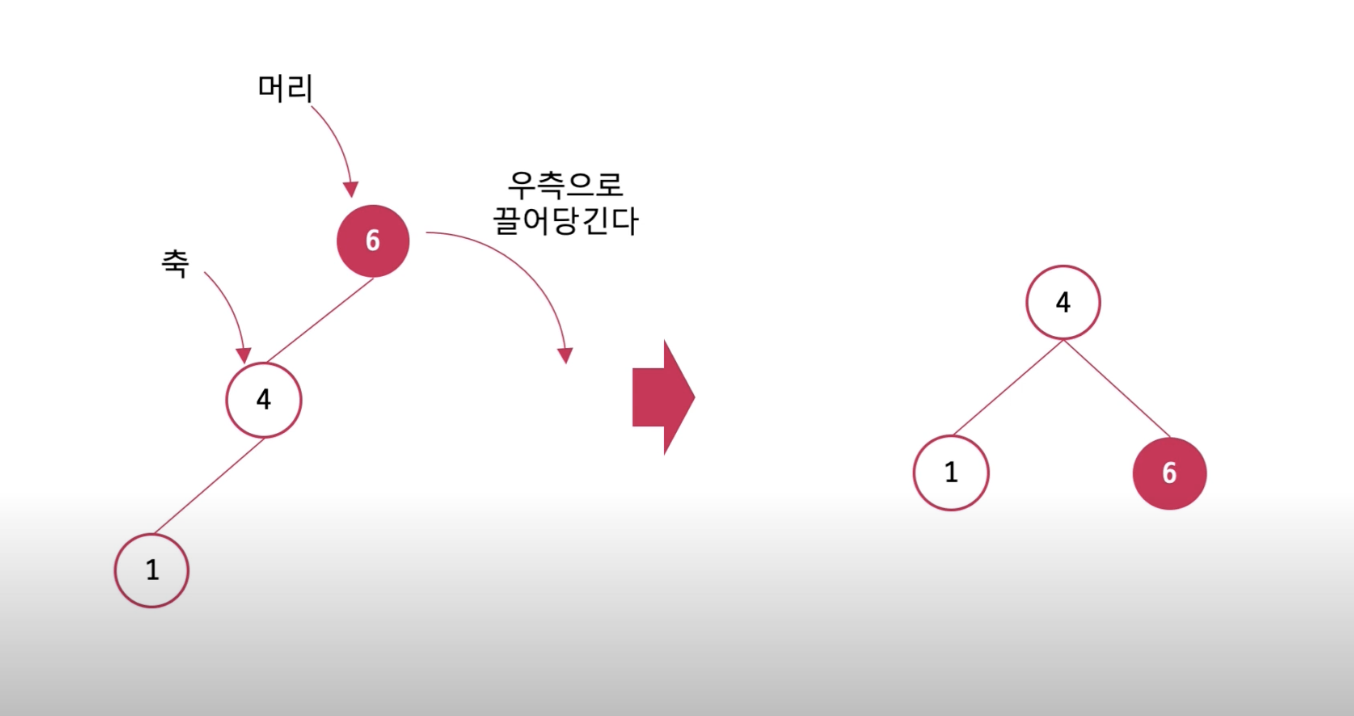
그림 처럼 4번 노드를 축으로 하고 6번 노드를 머리로 가정한 후 끌어당기는 것을 회전이라고 한다 회전을 마치면 우측 그림 처럼 조화롭게 트리가 변경된다. 이 회전도 위에 4가지 처럼 이름이 각각 부여되어 있는데 기본적인 개념은 크게 다를 것은 없다. 이름은
- LL 회전
- RR 회전
- LR 회전
- RL 회전
으로 이름 붙여져 있다.
LL 회전.
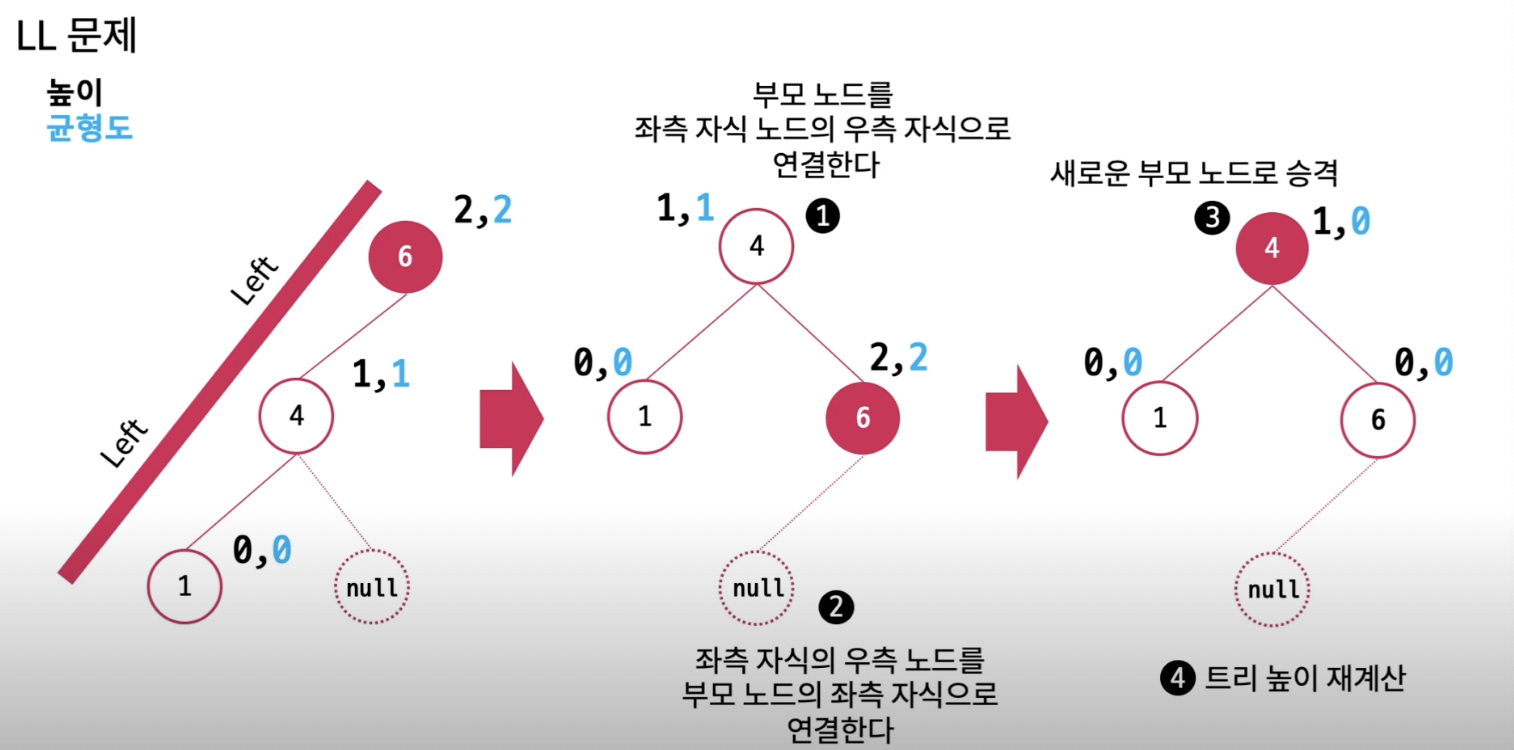
RR 회전.
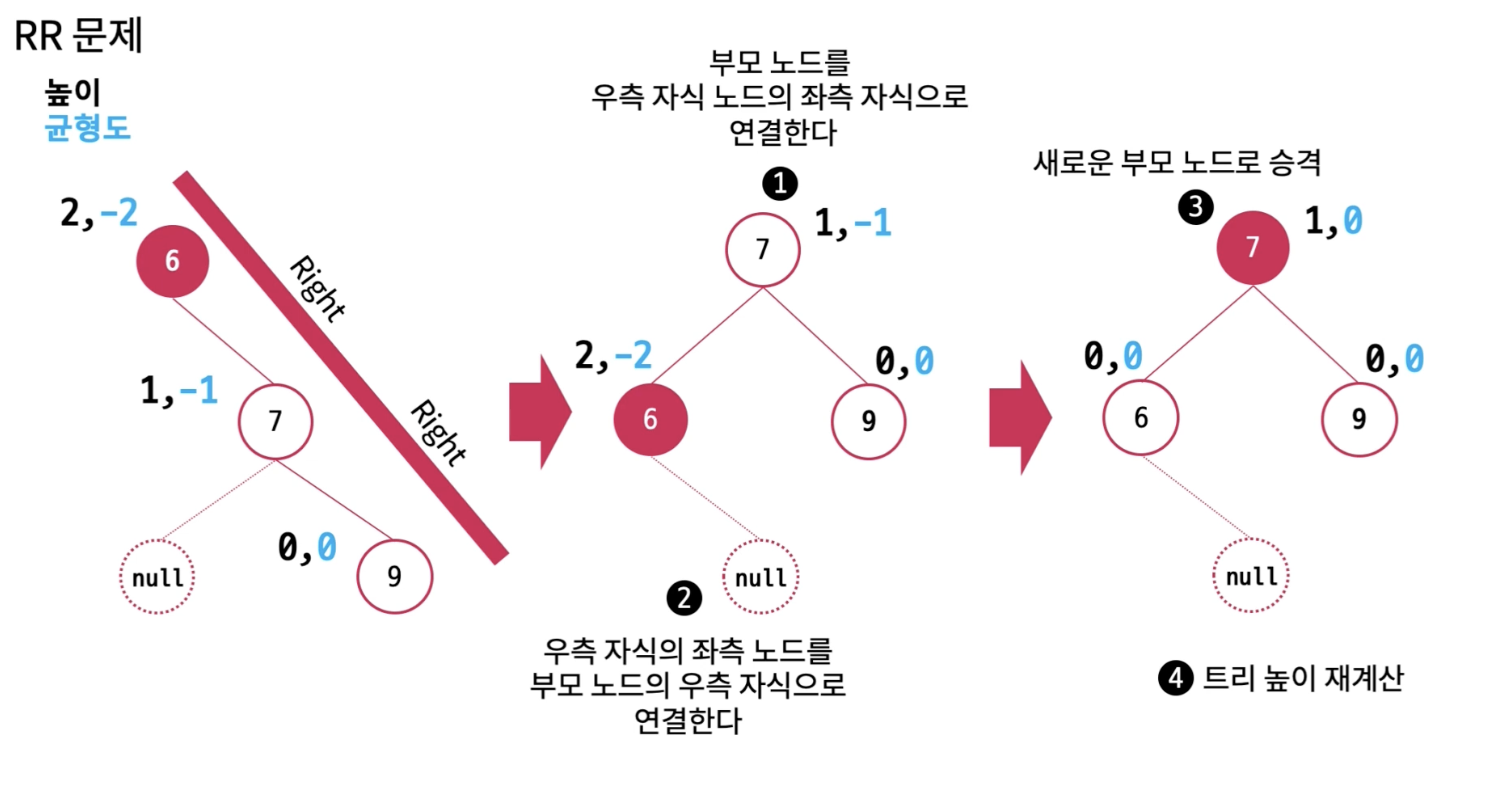
LR 회전.
여기서 부터는 살짝 다르다. LR문제는 좌측이 비대한 문제와 우측이 비대한 문제를 동시에 가지고 있다 따라서 이 문제를 해결하기 위해선 우측 비대 문제를 먼저 해결해야 한다. 이때 해결 하기 위한 것은 RR문제와 다른게 없기 떄문에 RR 회전을 하면 된다.
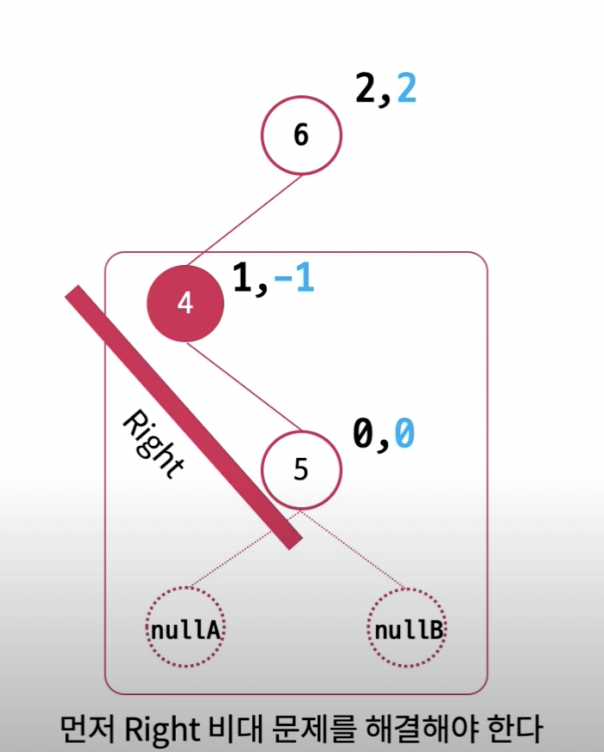
먼저 4번 노드를 부모 노드라 생각하고 4번 노드를 5번 노드의 좌측 자식 노드로 연결하고 우측 노드를 부모 노드의 우측 자식으로 연결한다. 그리고 새로운 부모 노드를 승격(바꾸고)하고 트리높이를 재계산 하면 된다.
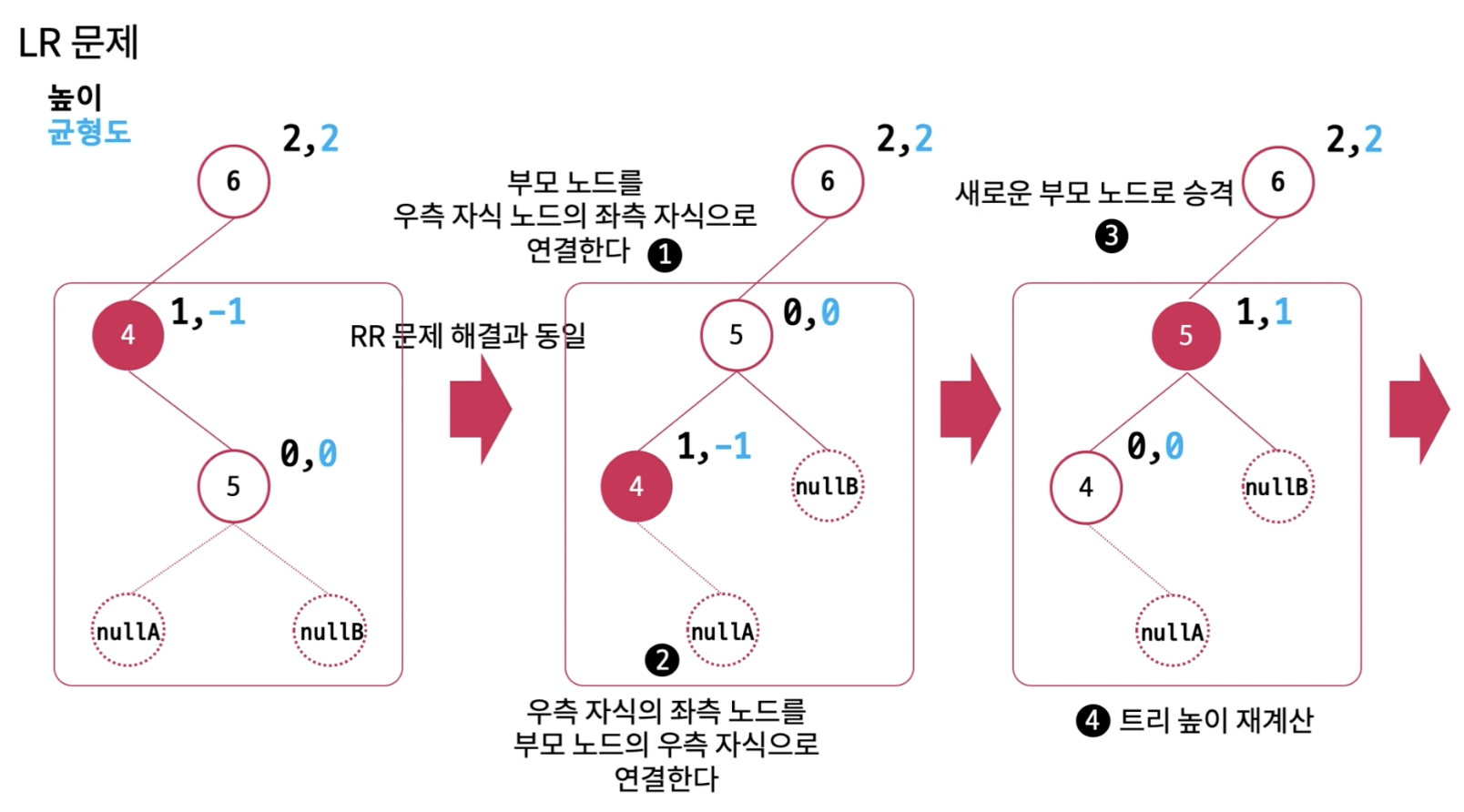
이제 우측 비대 문제를 해결했으니 나머지 남은좌측 비대 문제를 해결해보자.
이 부분도 LL회전을 하면 된다.
1). 이번엔 6번 노드를 부모노드라 생각하고 5번 노드를 축으로 끌어 당긴다.
2). 그런 다음 부모 노드를 좌측 자식 노드의 우측 자식으로 연결한다.
3). 좌측 자식의 우측 노드(nullB)를 부모 노드의 좌측 자식으로 연결한다.
4). 새로운 부모노드(5번)를 승격하고 트리 높이를 재계산한다.
RL 문제
RL 문제는 LR문제를 해결했을 때와 대칭적으로 해결하면 된다. 먼저 좌측 비대 문제 해결 -> 우측 비대 문제 해결 순서로 하면 되며 이때도 마찬가지로 각각 회전으로 푼다.
AVL 트리의 삽입과 삭제는 이진 탐색 트리와 동일하기 때문에 따로 설명할 것이 없다. 다음엔 이진 탐색 트리에 대해서 설명할때 이곳에 링크를 걸어두겠다.
참고 한곳.
코드라때 유튜브 - AVL 트리란?