1. 메모리
메모리란 ?
CPU와 연결되어 CPU에서 계산에 필요한 데이터를 읽고 계산한 후 그 결과를 다시 작성하는 저장소.
실제 메모리에서는 address라는 번호를 붙여서 데이터의 위치를 지정합니다.
CPU에서 메모리에서 데이터를 읽는 작업을 로드(load)라 하고 데이터를 읽을 때 메모리에서 데이터를 복사해서 읽기 때문에 원래 데이터는 메모리에 계속 남아있습니다.
CPU가 메모리에 데이터를 써넣는 작업은 스토어(store)라고 하고 데이터를 써 넣을 때 새로운 데이터를 기존 데이터에 덮어쓰기 때문에 원래 있던 오래된 데이터는 삭제됩니다.
2. 배열
배열이란?
메모리와 비슷한 데이터 구조입니다. 어떤 데이터라도 자유롭게 읽고 쓸 수 있는 특징이 있습니다. 데이터를 지정할 때는 인덱스(index)를 사용합니다.
배열에서는 데이터를 읽고 쓰는 과정은 메모리와 매우 유사합니다.
데이터를 꺼내어 읽을 때 데이터를 복사해서 읽기 때문에 원래 데이터는 계속 남아있습니다.
데이터를 써 넣을 때에는 새로운 데이터를 덮어쓰기 때문에 원래 있던 오래된 데이터는 삭제됩니다.
따라서 배열은 메모리를 이용할 때 기본으로 사용하는 데이터 구조입니다.
메모리 주소 구하는 방법
인덱스가 1인 데이터를 꺼내려할 때 인덱스 1에 해당하는 주소는 배열 맨 앞에 있는 주소에 인덱스 값 X 데이터 1개의 크기를 계산한 값을 더하면 됩니다.
배열 맨 앞에 있는 데이터의 주소 + 데이터 1개의 크기 x 인덱스
Python을 통한 배열 확인법
LISTEN 이라는 단어를 재배열하여 SILENT로 바꿔보겠습니다.
그리고 새로운 데이터 값으로 기존 값을 수정해보겠습니다.
Array = ['L', 'I', 'S', 'T', 'E', 'N']
print(Array[0], end = "")
print(Array[1], end = "")
print(Array[2], end = "")
print(Array[3], end = "")
print(Array[4], end = "")
print(Array[5])
print(Array[2], end = "")
print(Array[1], end = "")
print(Array[0], end = "")
print(Array[4], end = "")
print(Array[5], end = "")
print(Array[3])
Array[0] = 'A'
Array[1] = 'P'
Array[2] = 'P'
Array[3] = 'L'
Array[4] = 'E'
Array[5] = ''
print(Array[0], end = "")
print(Array[1], end = "")
print(Array[2], end = "")
print(Array[3], end = "")
print(Array[4], end = "")
print(Array[5])for문을 따로 쓰지 않고 직관적으로 확인할 수 있게 작성했습니다.
코드를 실행하면
다음과 같은 결과를 확인 할 수 있습니다.
Index를 통해 값을 출력하여 LISTEN을 SILENT로 출력되는것과 배열에서의 데이터 값 변경을 확인할 수 있었습니다.
3. 연결 리스트
연결리스트란?
연결 리스트는 데이터와 다음 데이터가 있는 곳을 모두 기록하는 데이터 구조입니다.
데이터가 순서대로 나열되고 포인터로 연결된다는 특징이 있고 연결 리스트를 줄여서 리스트라고 부릅니다.
데이터를 시대순으로 정렬하려면 데이터가 클 경우 매우 복잡하고 큰 일이 됩니다. 따라서 첫 데이터부터 마지막 데이터까지 순서대로 포인터를 사용하면 간단하게 할 수 있습니다.
-
단방향 리스트
위에서 말한 포인터가 한쪽 방향일 경우 다음에 오는 데이터만 관리하기 때문에 간단하게 처리할 수 있습니다. -
양방향 리스트
포인터가 양쪽 방향일 경우 데이터와 데이터 사이까지 모두 관리할 수 있고 역방향으로 거슬러 올라갈 수 있는 장점이 있습니다.
연결 리스트에서 데이터 삭제와 추가
데이터를 삭제할 때 다른 데이터를 옮기지 않아도 된다는 것은 매우 큰 장점입니다. 메모리에서 배치된 데이터를 옮기지 않고 포인터의 변경만으로 가능합니다.
데이터를 추가할 때 역시 이전 데이터와 연속된 위치가 아니더라도 데이터를 배치하고 포인터를 추가해주면 간단하게 추가가 가능합니다.
4. 트리 구조
트리구조란?
데이터 사이의 계층 관계를 표현하는 구조입니다.
트리 구조 알아보기
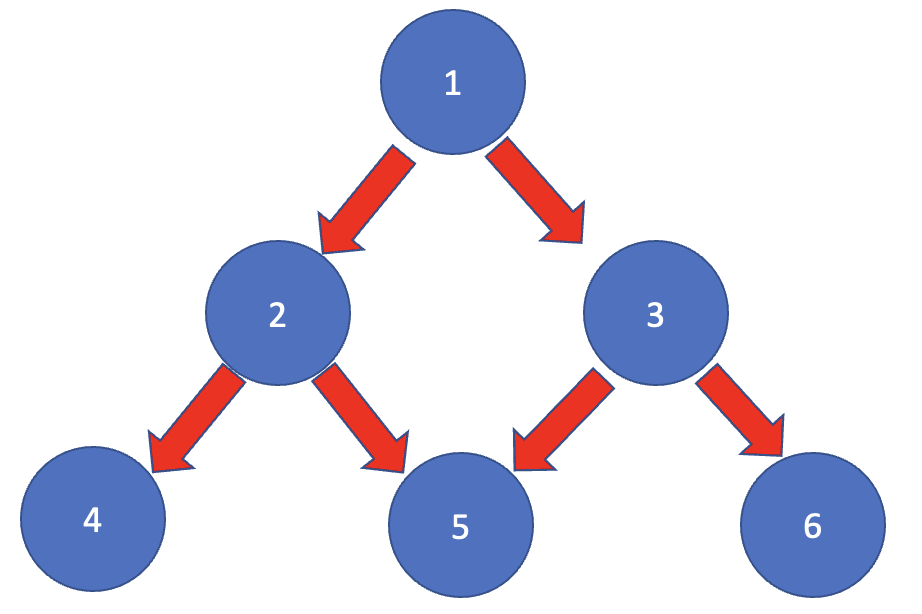
트리 구조는 크게 노드와 엣지 두가지로 구성되어 있습니다.
위 그림에서 동그라미가 노드, 화살표가 엣지를 나타냅니다.
노드는 크게 세가지로 나뉩니다.
가장 위 1번 동그라미를 루트 노드
중간의 2, 3번 동그라미는 부모 노드
가장 아래의 4, 5, 6번 동그라미는 리프 노드
트리 구조는 다음 3가지 조건을 만족해야합니다.
- 닫힌 회로가 없습니다. 즉 시작과 끝점이 서로 연결되어야 합니다.
- 루트 노드, 부모 노드, 리프 노드는 엣지로 연결됩니다.
- 부모 노드와 리프 노드는 각각 엣지 1개와 끝점 1개로 되어 있습니다.
5. 이진트리
이진트리란 ?
루트 노드, 부모 노드에서 시작하는 엣지가 1개 또는 2개인 트리 구조.
이진트리를 활용하여 간단한 수식 계산을 해봅시다.
예를들어 2 * (4 + 6) 을 계산하면, 곱셈 계산이 우선이지만 ( ) 가 있기 때문에 ( )로 묶인 4 + 6을 우선 계산하고 이후 나머지를 계산하면 됩니다.
이를 이진트리 구조로 나타내면
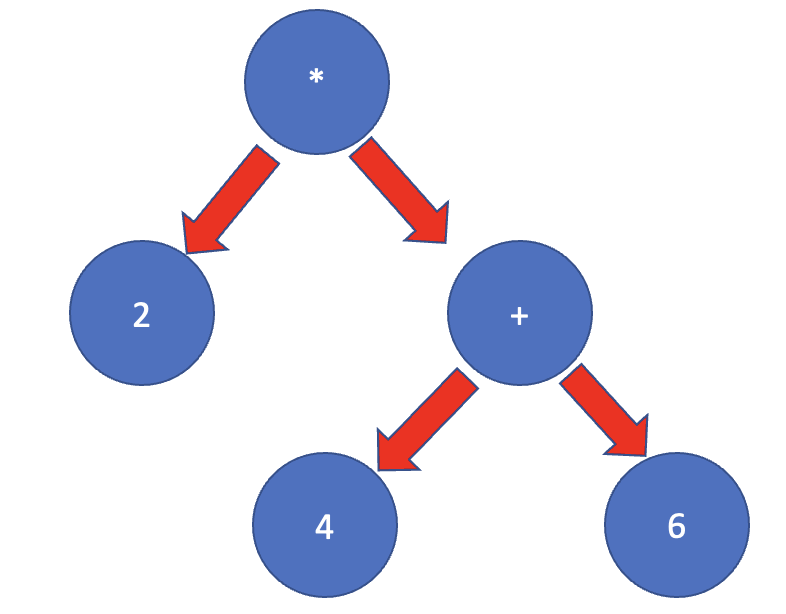
다음과 같이 표현할 수 있습니다.
이외 다양한 계산을 이진트리로 표현할 수 있습니다.
