Monad는 어떻게 정의할 수 있을까?

Monad

Monad: 다음의 연산들이 정의된 Functor

unit: T -> M<T> (return in Haskell)

flat: M<M<T>> -> M<T> (join in Haskell)

• Functor에 unit하고 flat추가한게 모나드다.
• 직관적으로만 이해하고, unit, flat이 어떤 조건을 만족해야 하는지는 가장 아래에서 알아보자.

Monad 함수의 추가 조건

• unit, flat 함수가 가져야할 추가 조건에 대해 설명한다.

Naturality for unit.

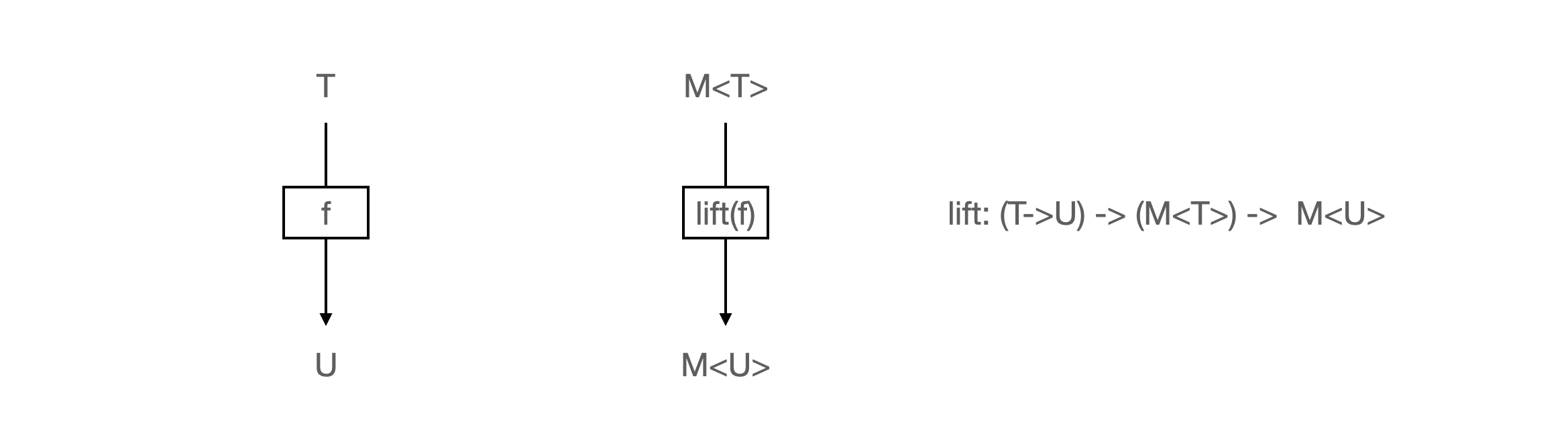
• T->U로 가는 함수를 f라고 정의해보자.
• lift함수에 f를 인자로 넣어서 나오는 반환 값의 타입은 M<T> -> M<U>이다.
• 그렇다면 이 반환 함수에 M<T>를 인자로 넣어서 나오는 반환 값의 타입은 M<U>이다.

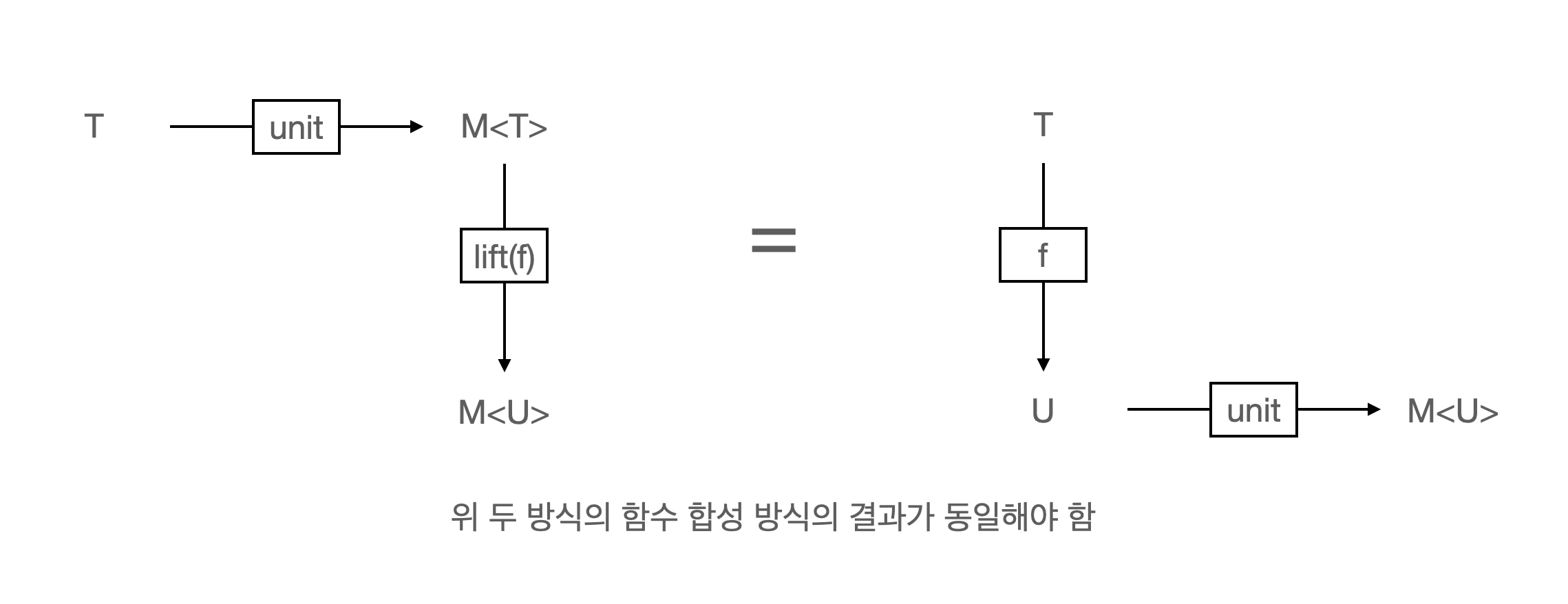
• 자연성을 만족한다는 말은,
• f를 적용한 후 unit함수를 적용한 것과
• unit함수를 통해 M<T>를 M<U>로 바꾸고, f를 적용한 것이 같다는 말이다.

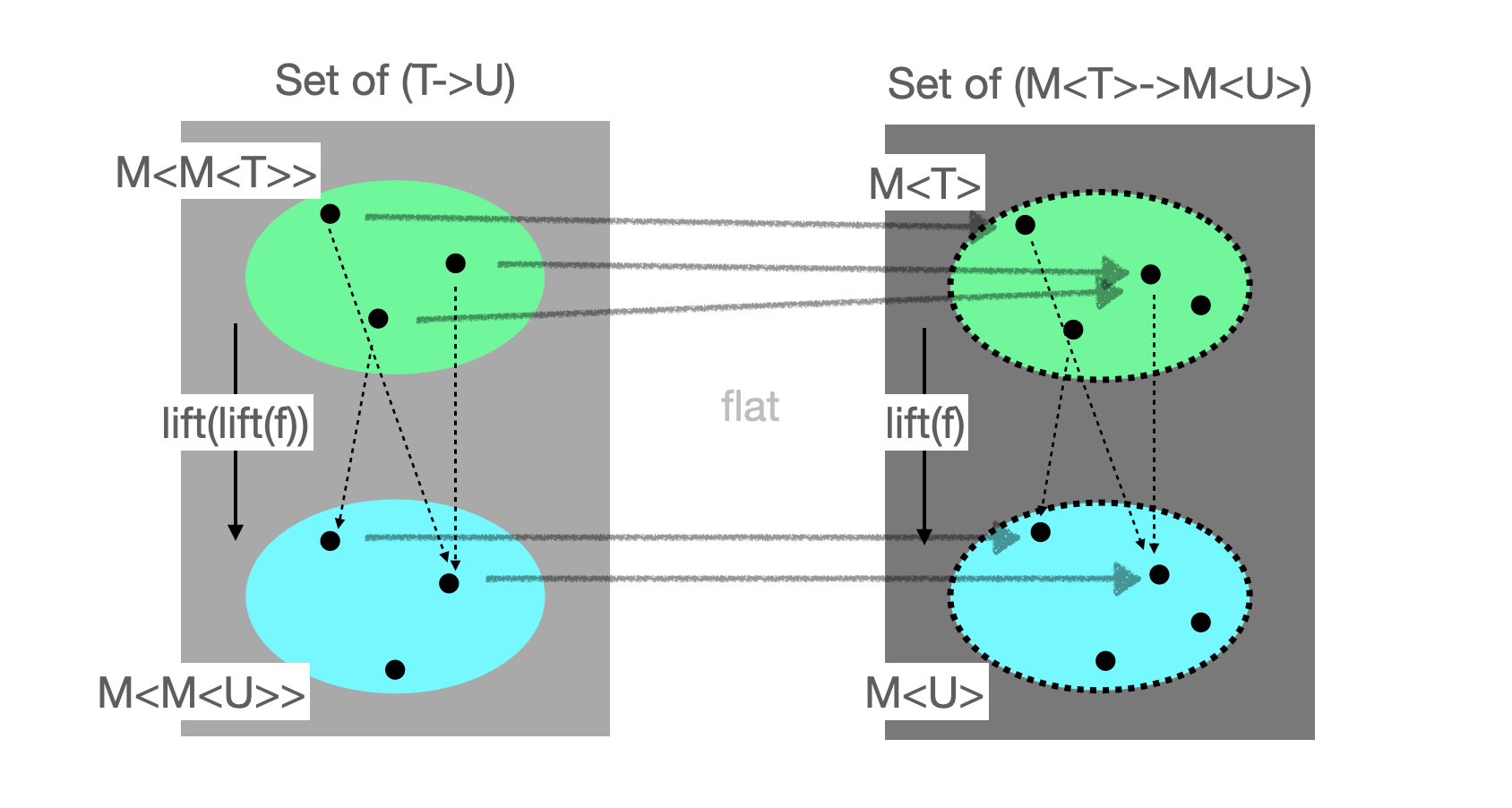
Naturality for flat

naturality for flat.

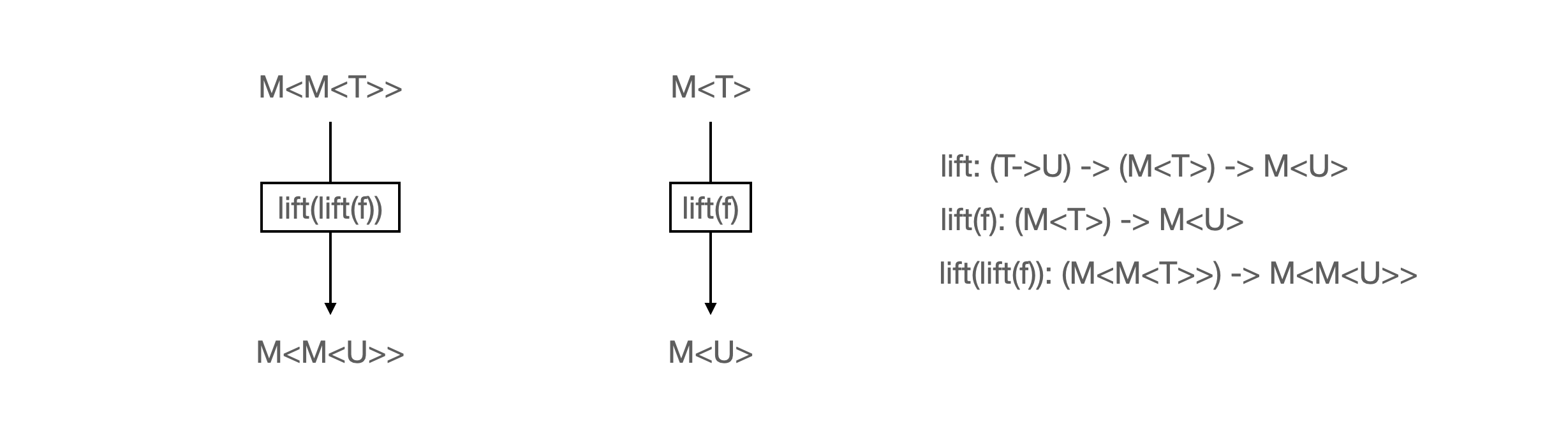
• 마찬가지로 T->U로 가는 함수를 f라고 정의해보자.
• lift함수에 f를 인자로 넣어서 나오는 반환 값의 타입은 M<T> -> M<U>이다.
• 당연히 M<T>를 위 함수에 넣으면 반환값은 M<U>이다.
• M<M<T>>를 M<M<U>>로 바꾸려면 lift(lift(f))를 적용해야 한다.

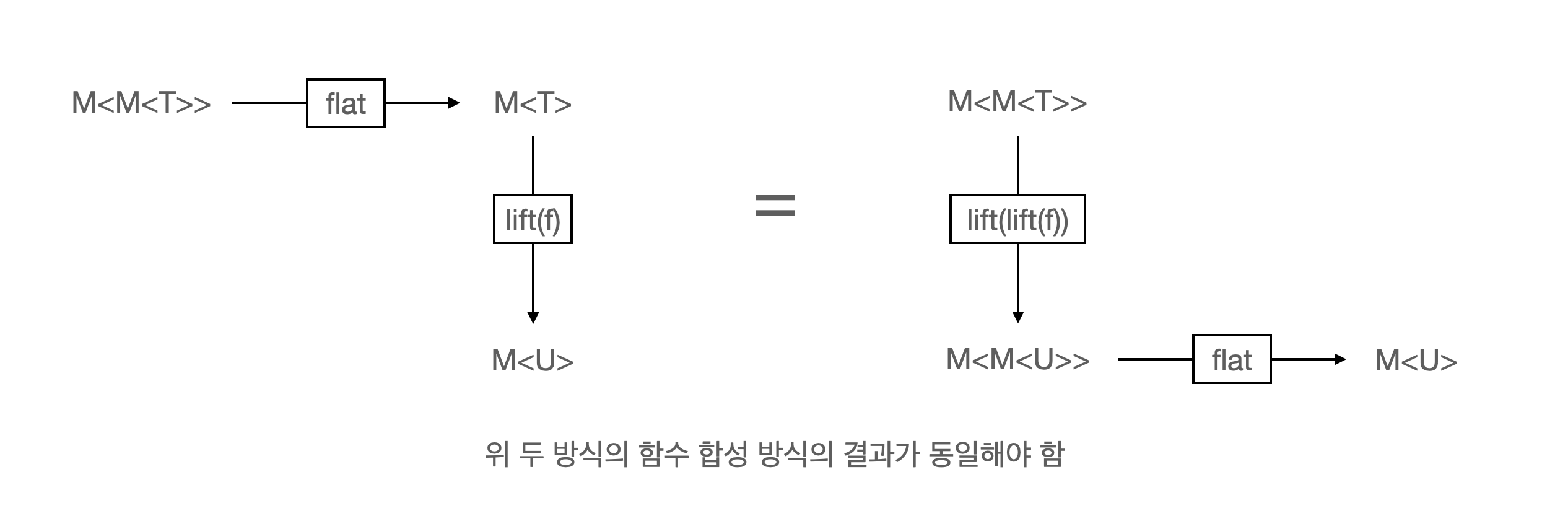
• 자연성을 만족한다는 말은,
• lift(lift(f))를 적용한 후 flat함수를 적용한 것과
• flat 함수를 적용하고 lift(f)를 적용한 것이 같다는 말이다.

Identity

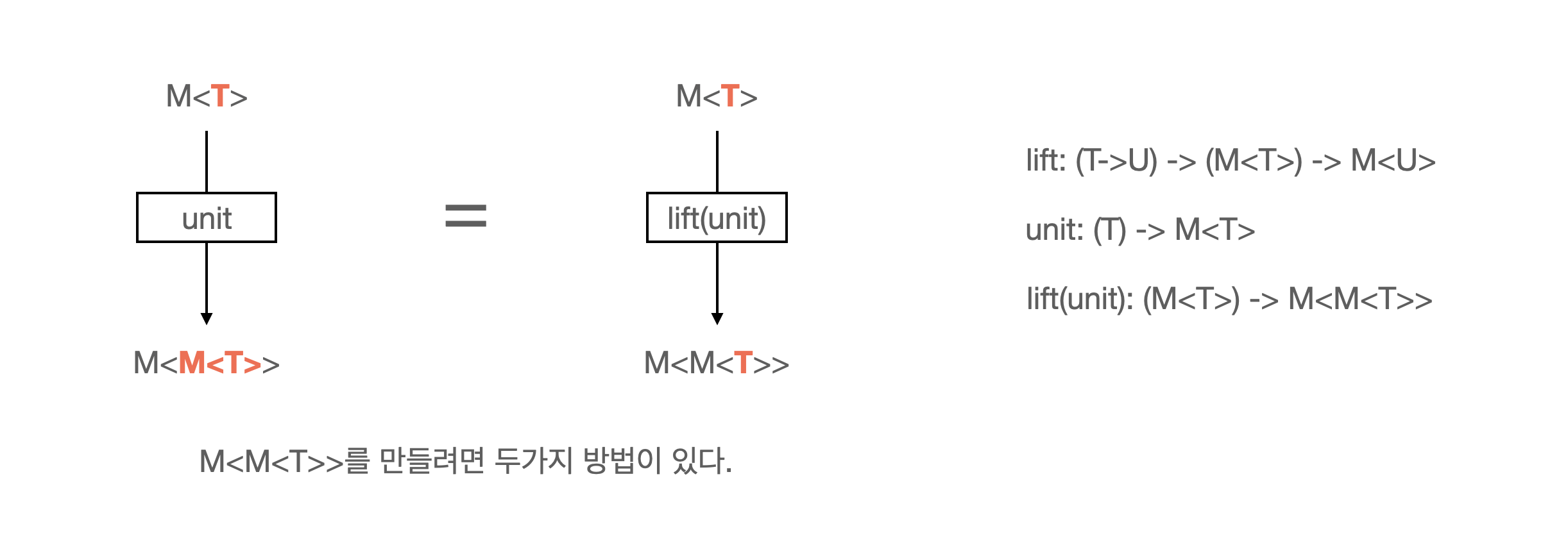
• M<T>를 M<M<T>>로 바꾸는 방법은 두개가 있다.
• unit을 적용하거나, lift(unit)을 적용하거나.
  • 지금 생각해보니 unit이라는 함수의 이름이 이 때문인 듯 하다.
  • lift를 여러번 적용했을 때의 함수와 unit을 적용했을 때의 함수가 같다.
  • 타입이 한꺼풀 싸져있는 것으로 보이지만, Generic이기 때문에 어떤 타입도 들어갈 수 있기 때문에 구조적으로 같다.
• unit을 적용한다는 것은 M<T> 타입 자체에 함수 동작을 걸어버리는 것이고,
• lift(unit)을 적용한다는 것은 T타입에 unit함수를 적용한다는 가정을 한 상황에서 lift를 통해 한차원 높인 상태의 함수를 만들고 적용한다고 생각할 수 있겠다.

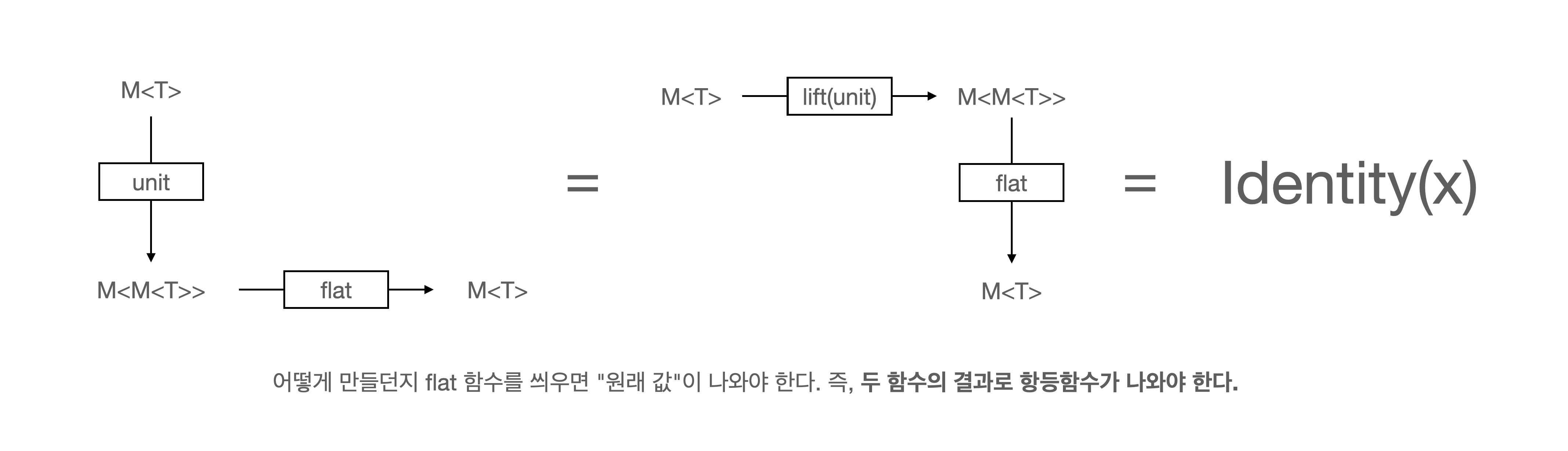
• 이렇게 나온 M<M<T>>에 flat함수를 걸었을 때 결과는 M<T>로 나와야 한다는 것이 항등성이다.
• 즉, 왼쪽과 오른쪽의 두식의 결과는 항등함수로 나와야 하며, 그 결과는 같아야 한다.

Associativity

• M<M<M<T>>>를 M<M<T>>로 바꾸는 방법은 두개가 있다.
• flat을 적용하거나, lift(flat)을 적용하거나.
• 이 순서를 바꿔서 연산하면 결과값은 다를 수 있다.

• 하지만 그 결과를 다시한번 flat으로 내렸을 때 나오는 결과는 반드시 같아야 한다.

위 내용이 의미하는 바

Semantics in Naturality

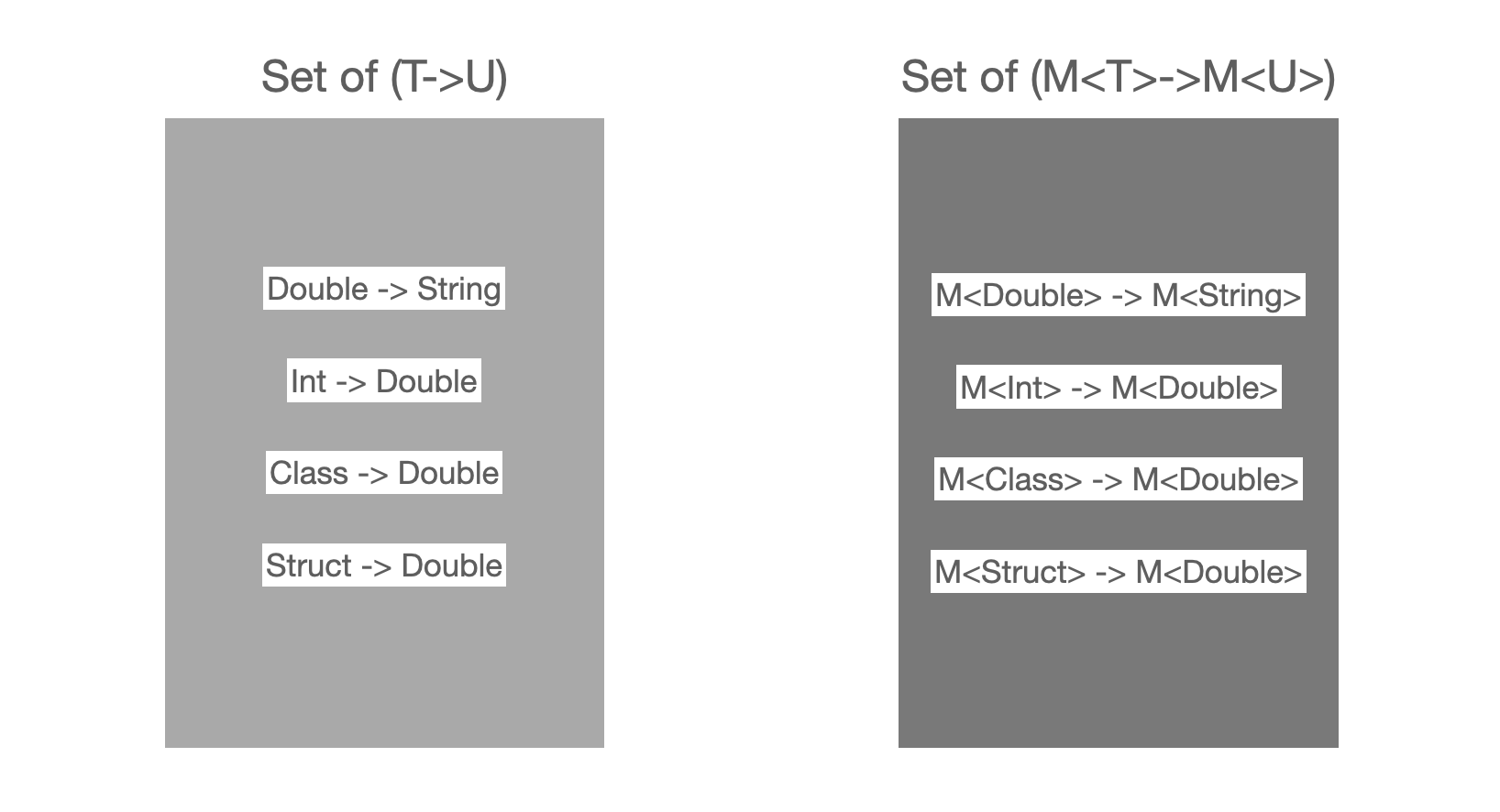
• T->U로 보내는 함수들의 집합을 하나 생각해보자.
• T, U는 제네릭으로 표현되었으니, 하나하나 구체 타입을 넣어보면 원소들이 있는 공간이 떠오를 것이다.
• 마찬가지로 M<T>->M<U>로 보내는 함수들의 집합도 생각해보자.
• 아마 수도없이 많을 것이다.
• 그리고 이 사상관계의 로직도 수도없이 많을 것이다.
  • Double->String으로 가는 함수 원소의 개수도 엄청많은데, 사실 그 변형 함수 로직의 다양성까지 포함해야한다.
  • 그렇다면 이 집합은 무한집합일 것이다.

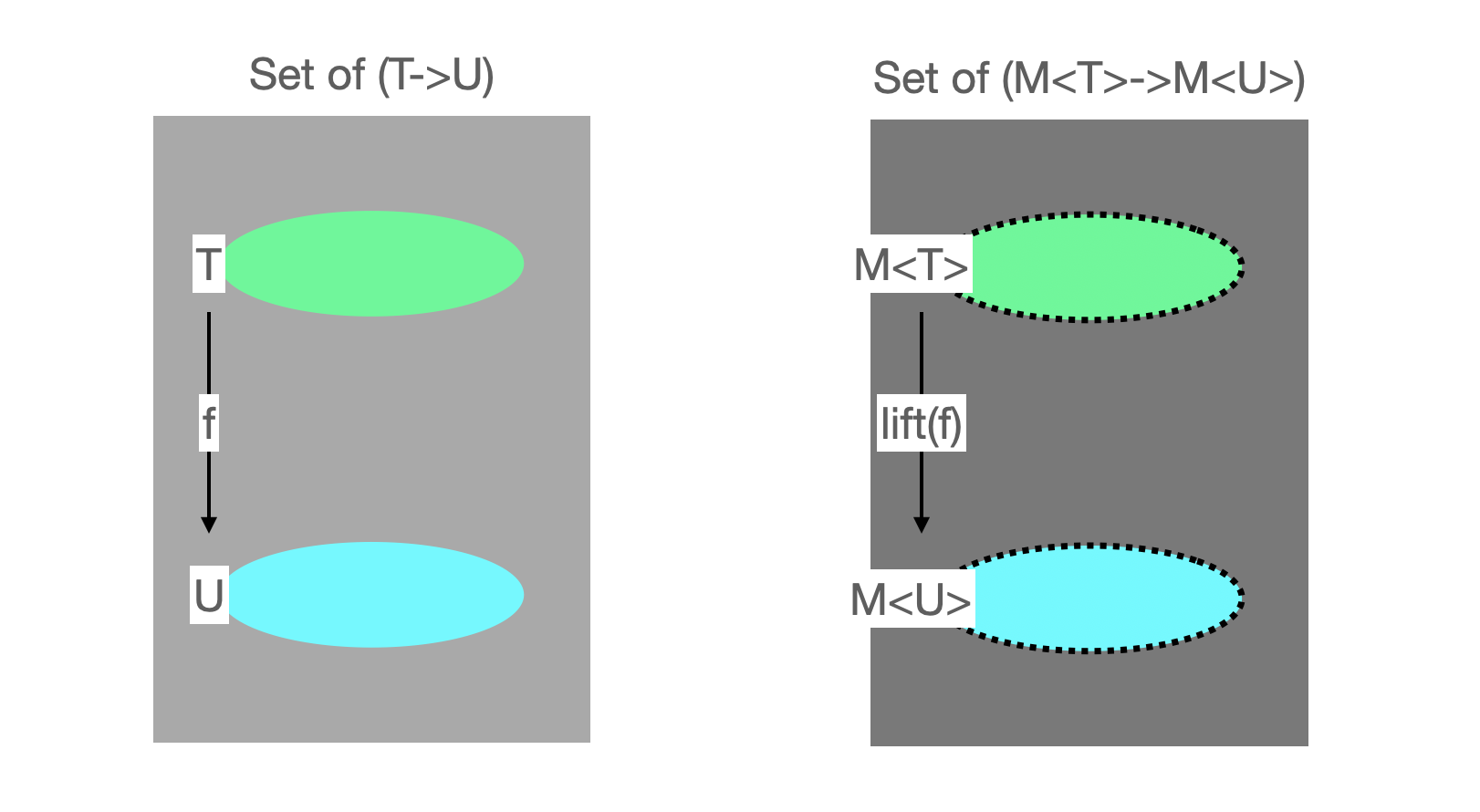
• 이 모든 원소를 예를 들면서 설명할 수 없으니,
• T->U로 가는 함수 원소를 대표할 수 있게 위와 같이 그림을 그려보았다.
• 함수의 형태에 따라 원소 개수가 늘어난다 했으니 이 역시도 f와 같은 형태로 변수로 표현했다.
• 이렇게 왼쪽 집합이 정의 된다면, Monad는 일단 Functor니까 오른쪽 집합도 당연히 정의될 수 있다.
• 이 때 변환에 대응되는 것은 lift(f)이다.

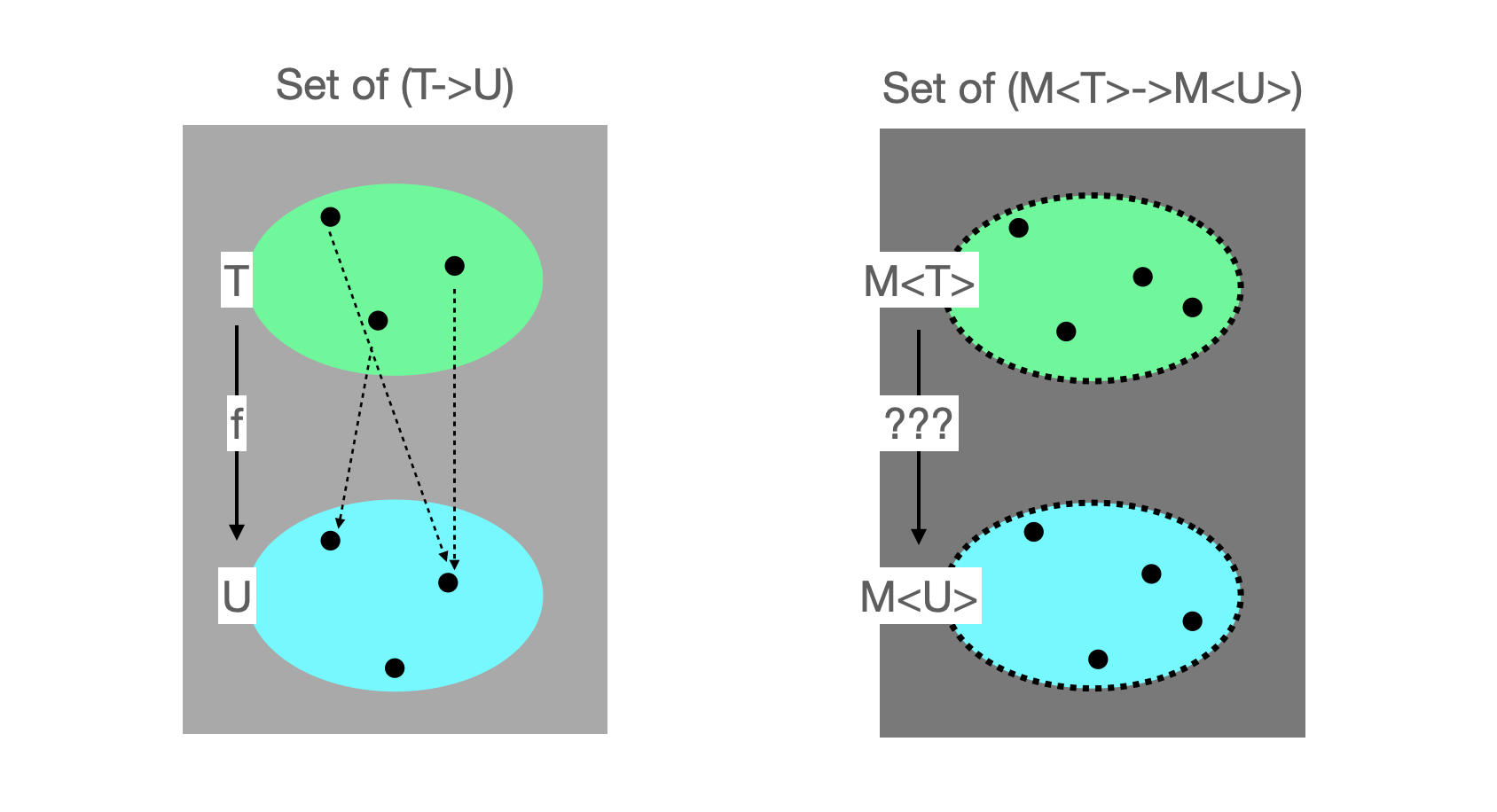
• 각 타입은 또 그 안에 들어갈 수 있는 값들을 대표하는 집합으로 생각할 수 있다.
• 가령 Double 자료형은 1.0, -3000과 같은 다양한 실수값을 반영할 수 있는 집합의 개념이다.
• 이렇게 타입에 해당하는 값을 "점"의 형태로 그림에 표현했다.
• 그리고 f라는 변환은 값들이 U의 공간에 특정 점에 매핑된다고 할 수 있다.
• 그럼 M<T>->M<U>에 대응되는 원소는 어떻게 그릴 수 있을까?
• 일단 원소가 있을 거라는 건 쉽게 예상할 수 있다.
• 그럼 모나드 인 경우 이 매핑관계 (f에 대응되는 녀석)은 무엇이 될 수 있을까?

unit

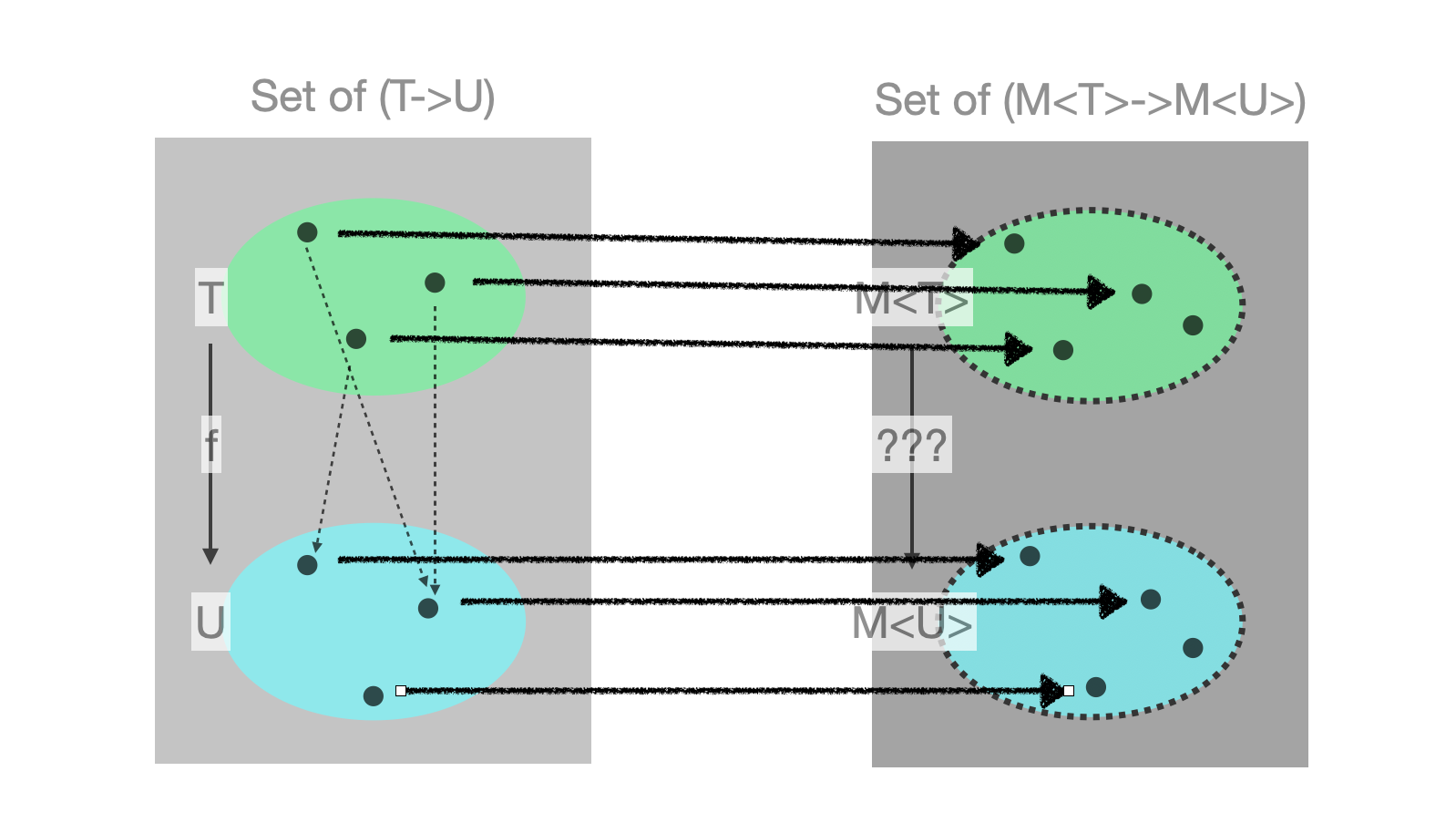
• 그 전에 먼저 Monad가 되기 위한 조건인 unit함수의 의미부터 알아보자.
• unit 함수는 함수를 원소로 갖는 두 집합 사이의 관계를 정의한다.
• 이 관계는 함수를 원소로 갖는 집합의 인자에 해당하는 타입을 모나드 타입의 원소로 연결해주는 역할을 한다.

lift

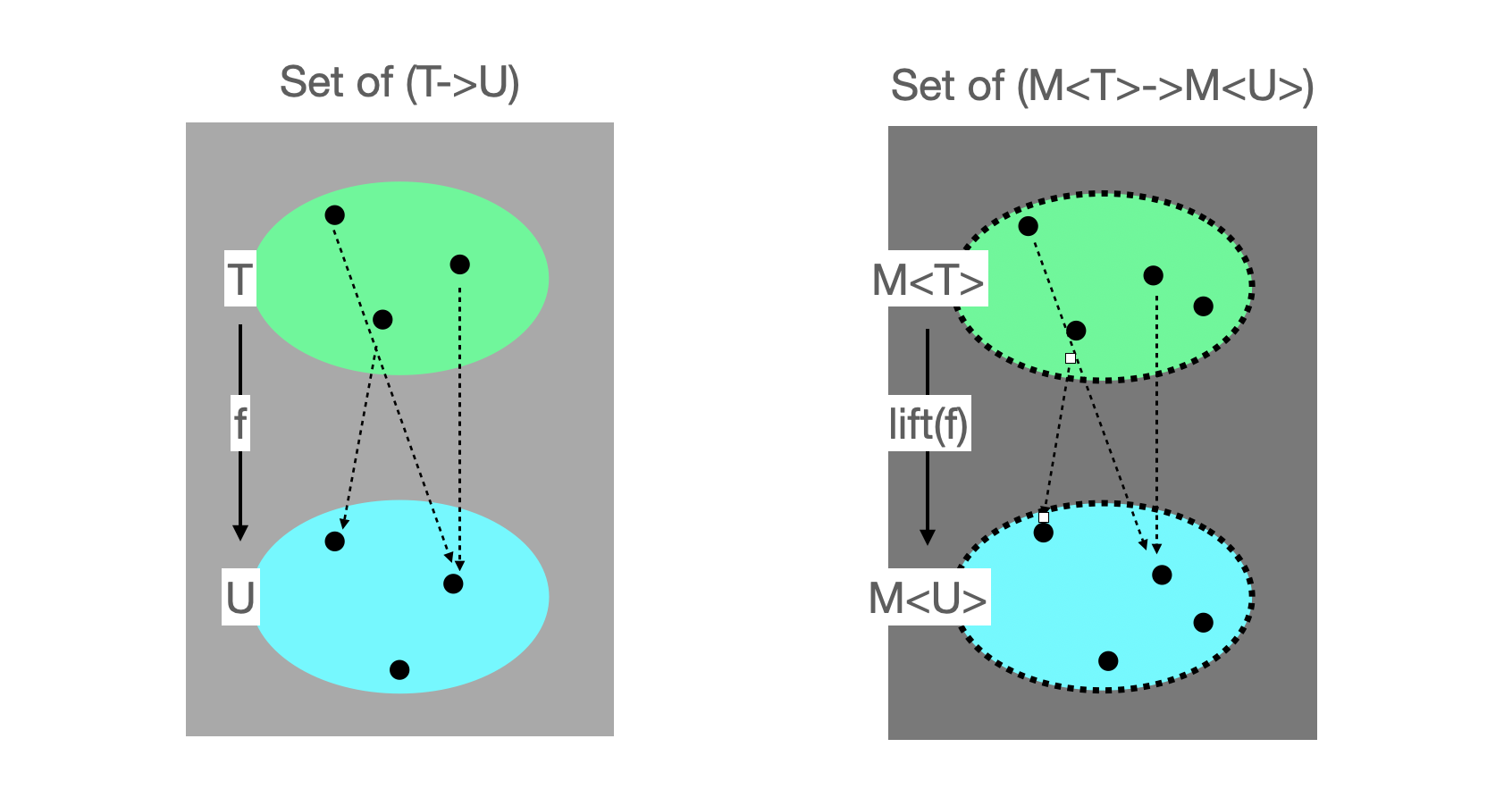
• 그렇다면 lift은 어떻게 도식할 수 있을까.
• T와 U사이에 f라는 논리적 관계가 정의되어 있다면,
• T와 U를 unit한 값들 사이에서도 lift(f)로 표현되는 논리적 관계가 존재해야 한다.
  • 모나드가 되기 위해서는 그래야 한다.
• 이러한 관계가 말이 되기 위해서는 unit이라는 관계는 값들 사이의 논리적 관계를 전부 보존하는 변환이어야 한다.
• 즉, T타입을 모나드화 하는 unit연산의 수행 결과는, T의 의미를 전부 보존해야만 한다.
• 그럴려면 값의 의미를 유지한 채 타입만 바꾸는 변환이 아니면 불가능하다.
• 예컨데 Int을 Double로 바꾸는 연산.
• 즉, M<T>는 T 또는 T와 논리적으로 동등한 개념을 지칭하는 타입이라는 것을 알 수 있다.

flat

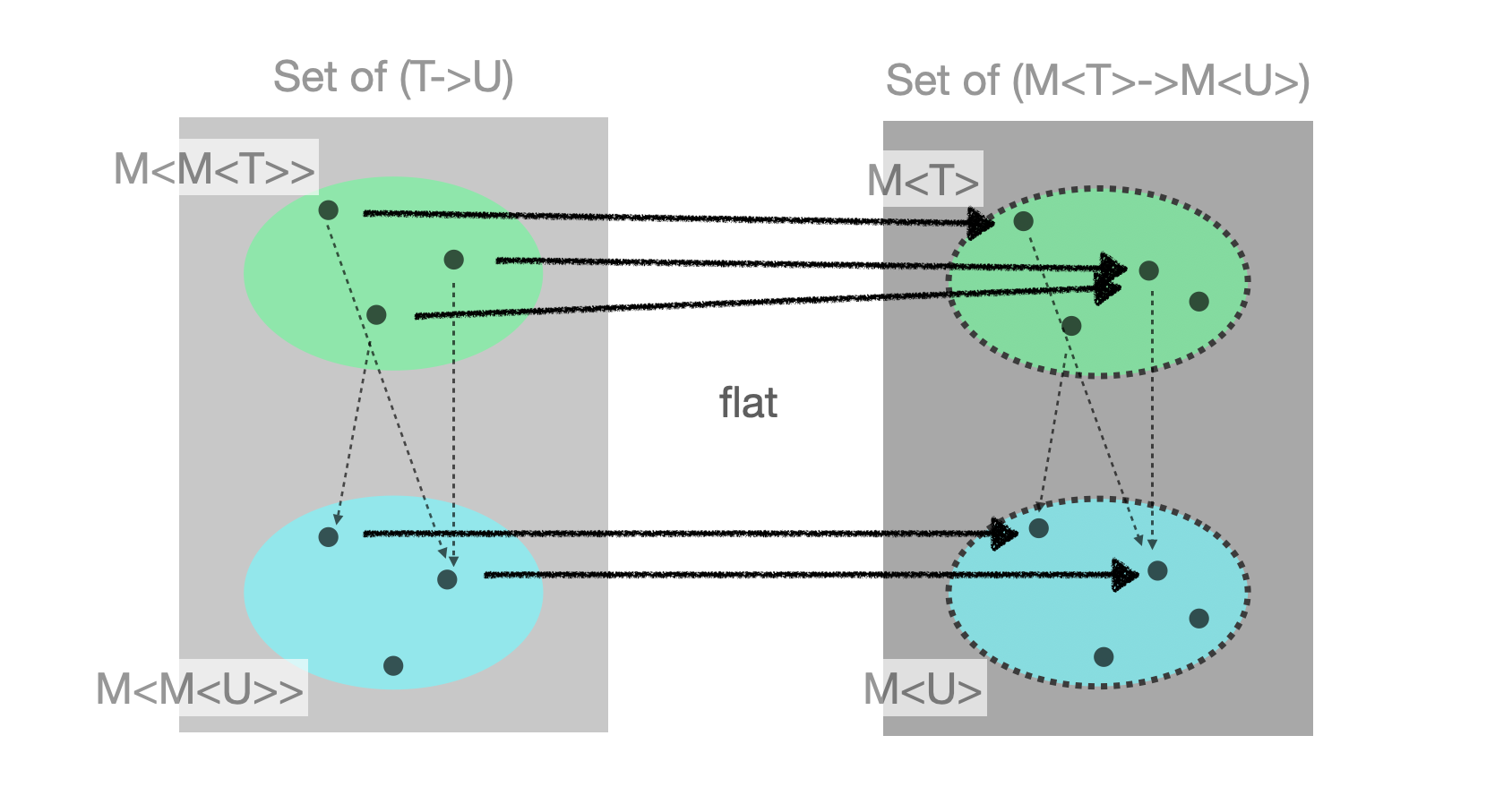
• flat은 M<M<T>>를 M<T>로 바꿔주는 연산이다.
• 이 때, 모든 논리적 관계를 보존할 필요는 없다.
  • 차원을 낮추는 행위이기 때문에 애초에 이상적으로는 불가능하다.

• 하지만 lift(lift(f))로 표현되었던 연산의 "일부" 논리적 관계는 보존해야 한다.
  • 모나드의 정의에서 원하는게 그거다.
• 그러러면 flat이라는 함수는 값의 의미를 적어도 일부는 보존한 채 M<M<T>>를 M<T>로 바꾸는 변환이 되어야 한다.

의미론적 고찰의 결론

• 위에서 한 작업은 모나드의 정의를 토대로 도식화한 뒤, 그 의미를 찾아보는 과정이었다.
• 이 결과 얻어지는 의미론적 결론은 다음과 같다.

1. M<T>는 T의 의미를 확장한 의미를 가진 타입이어야 한다. (unit)
2. M<M<T>>는 어떤 의미에서는 M<T>와 같이 간주될 수 있어야 한다. (flat)

예시

Optional

• T의 의미를 확장한 Optional의 의미는 T 또는 nil이다. 즉, 포함한 채로 확장한 의미이다.
• Optional<Optional<T>>는 Optional<T>와 같이 간주될 수 있다.

Array

• T의 의미를 확장한 Array의 의미는 T의 집합이다. 즉, 포함한 채로 확장한 의미이다.
• Array<Array<T>>는 Array<T>와 같이 간주될 수 있다.
  • 앞에서도 말했듯 완전한 정사영은 불가능하다.
  • 차원 축소의 개념이기 때문.
  • 하지만 의미론적으로 논리적 관계는 보존할 수 있다.
  • 추가적으로 순서의 개념까지 논리적 관계를 보존하는 것이 더 정확하겠다.

실전적 결론

모나드는 어떠한 개념에 대한 논리적 확장으로, 오직 한번만 의미있게 적용 가능한 것들을 통칭하는 개념이다.

M이 Monad라면,

1. T의 의미를 확장할 수 있는 방법이 정의되어 있어야 한다.
2. 같은 방법으로 재차 확장했을 경우, 다음의 의미가 있어야 한다.
   a. 의미 없거나
   b. 의미가 같거나
   c. 어떤 관점에서는 같다고 볼 수 있음

구현

• 이상적으로는 상위 클래스 정의해서 하는 게 맞다.
• 하지만 프로그래밍 언어에 따라 이 구현은 달라진다.
• 보통 타입 내에 연산을 추가하여 (flatMap) 구현하는 경우가 많다.

Optional

unit

extension Optional {
    internal func unit(_ t: T) -> T? {
        .some(t)
    }
}

flat

extension Optional {
    internal func flat<T>(_ oot: Optional<Optional<T>>) -> Optional<T> {
        switch oot {
        case .none:
            return .none
        case .some(let ot):
            return ot
        }
    }
}

부가설명

Natural transformation

• 앞에서 연산이 자연성(naturality)을 만족해야 한다고 했다.
• 수학적 명확한 정의는 내 머리로 이해가 정확하게 안되서 첨부한다.

"자연성(naturality)"은 수학에서 함수나 변환자(transformer) 사이의 관계가 다른 수학적인 구조를 변형해도 변환의 특성을 유지하는 것을 의미합니다. 이러한 관계는 수학적인 구조 간에 일관성을 유지하며 변환을 적용할 수 있도록 해줍니다.

예를 들어, 두 개의 함수 F와 G가 있고, 어떤 구조에서 F와 G를 적용할 때 일관성이 유지된다고 가정해봅시다. 그렇다면 이 두 함수 사이의 관계는 "자연성"을 가진다고 할 수 있습니다. 즉, 어떤 변환을 적용하더라도 결과가 일관성 있게 유지되는 것입니다.

Identity

모나드(Monad)의 항등성(identity law)은 함수형 프로그래밍에서 모나드가 가져야 하는 중요한 특성 중 하나입니다. 모나드는 데이터 형식을 다루는 추상적인 개념으로, 값을 감싸거나 조작하는 데 사용됩니다. 이 때 모나드의 항등성은 모나드의 동작을 보다 안정적이고 일관적으로 만들어줍니다.

모나드의 항등성은 크게 두 가지 관점에서 설명될 수 있습니다

Left Identity (왼쪽 항등성)

어떤 값을 모나드로 감싼 후에 해당 모나드를 특정 함수에 적용하는 것과, 그 값을 바로 그 함수에 적용하는 것은 같아야 합니다. 즉, m이라는 모나드와 함수 f가 있다면, 아래와 같은 관계가 성립해야 합니다

flatMap(unit(x), f) == f(x)

여기서 unit(x)는 값을 모나드로 감싸는 역할을 하는 함수입니다. flatMap은 모나드의 값을 함수에 적용하는 연산을 나타내며, f는 임의의 함수를 나타냅니다.

Right Identity (오른쪽 항등성

모나드에 값을 적용한 뒤에 모나드를 벗겨낸 결과와, 그 값을 바로 모나드에 감싸지 않은 결과는 같아야 합니다. 즉, m이라는 모나드와 함수 f가 있다면, 아래와 같은 관계가 성립해야 합니다:

flatMap(m, unit) == m

여기서 unit은 값을 모나드로 감싸는 역할을 하는 함수입니다.

Reference

• 모나드의 모든 것
• FunctionalProgramming
• Natural_transformation