SEC Serialization

최완식·2023년 2월 13일

<sec:>Byte Ordering Compressed SEC Serialization public key

Bitcoin Programming

목록 보기

6/8

비밀키, 공개키, 서명, 그리고 검증 방법까지 알아보았다. 하지만 이러한 값을 가지고 있기만 해서는 결제라는 행위가 이루어질 수 없다. 어딘가로 보내야 한다. 그때 필요한 기술인 직렬화를 알아보자.

직렬화

특정 객체의 정보를 비트로 변환하는 것
이 과정에서 부호화, 복호화가 필요하기 때문에, 일련의 합의하는 규칙이 필요하다.

비압축 SEC 형식

일단 S256Point를 직렬화해보자.
해당 클래스는 공개키를 표현하게 되는 클래스이다.
공개키는 타원 곡선위의 한 좌표를 의미하기 때문이다.
이런 공개키를 직렬화하는 형식은 SEC(Standard for Efficient Cryptography)라 한다.

방법

$P = (x, y)$ 에 대해 비압축 SEC 표현 방식은 다음과 같다.

0x04의 1바이트 prefix로 시작한다.
$x$ 를 32바이트 Big Endian 정수로 표현한다. (16진수로 64자)
$y$ 를 32바이트 Big Endian 정수로 표현한다. (16진수로 64자)
1, 2, 3을 한데 더한다.

047211a824f55b505228e4c3d5194c1fcfaa15a456abdf37f9b9d97a4040afc073dee6c89064984f03385237d92167c13e236446b417ab79a0fcae412ae3316677

- marker: 04
- x: 7211a824f55b505228e4c3d5194c1fcfaa15a456abdf37f9b9d97a4040afc073
- y: dee6c89064984f03385237d92167c13e236446b417ab79a0fcae412ae3316677

Big Endian, Little Endian에 대한 설명은 Byte Ordering을 참고하자.
쉽게 말하면, 특정 데이터를 비트로 변환할 때 이를 나열하는 순서에 대한 것이다.
Big Endian의 경우 우리가 일반 숫자를 쓰듯, 앞에 큰 단위를 의미하는 숫자가 오고,
- 0x182 = 2561 + 168 + 1*2 = $386_{(10)}$
Little Endian의 경우 그 역순으로 된다.
- 0x182 = 11 + 168 + 2*256 = $641_{(10)}$
비트를 어떤 순서로 나열하느냐에 따라 이를 파싱하여 나오는 결과값이 상이하기 때문에, 어떠한 규칙으로 저장하는지는 중요한 문제가 된다.

구현

class S256Point(Point):
...
    def sec(self):
        return b'\x04' + self.x.num.to_bytes(32, 'big') + self.y.num.to_bytes(32, 'big')

b'\x04'는 python에서 bytes 객체를 생성하는 방법이다.
자세한 것은 47.3 bytes, bytearray 사용하기를 참고하자.
to_bytes()함수는 정수형을 bytes 형으로 바꾸는 메서드이다.
- 32: 길이
- 'big': 방식

압축 SEC 형식

공개키는 결국 타원 곡선 위의 한 점이다.
이 특성을 알고 있다면 굳이 공개키를 압축할 때, $(x, y)$ 두개의 값을 담아서 보낼 필요가 없을 수 있다.
대신 $x$ 값 하나만 보내고, 받는쪽에서 이를 계산하여 $y$ 값을 얻으면 된다.
- 다만 연산력이 추가로 필요하기 때문에, 시스템에 따라 저장 비용이 중요한지 계산 비용이 중요한지 판단할 필요는 있다.

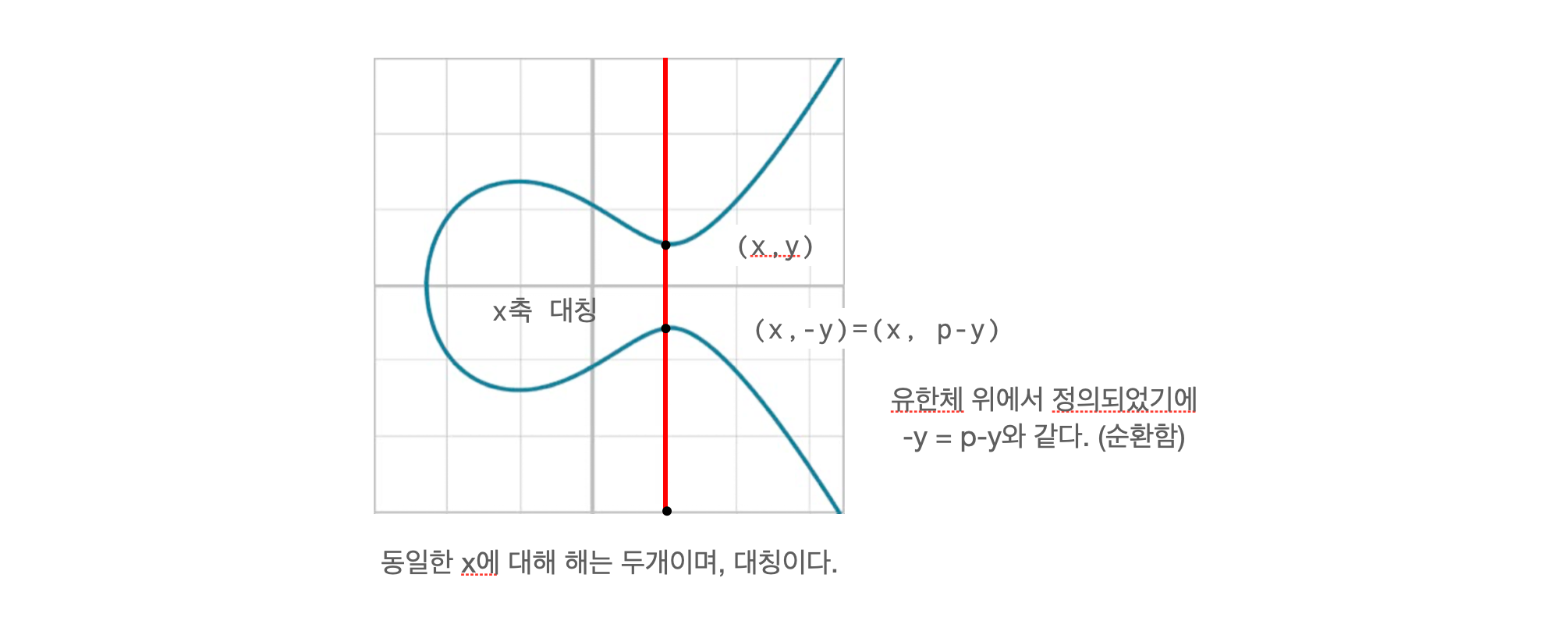
압축 SEC 형식의 핵심 아이디어는, x만 제공하고 그에 따른 y값은 계산하자.
그리고 그 y값의 결정은 타원 곡선 위에서 동일 x에 대한 해들의 대칭적 특성을 사용하여 최소한의 정보만 추가하여 결정짓자는 것이다.
쉽게 생각해보자.
x가 고정되어 있을 경우 타원 곡선에서 해는 두개이며 대칭이다.
유한체에서 p의 값은 2보다 큰 소수이다. 즉 "홀수"이다.
위쪽의 해의 y값이 홀수인 경우
- 아래쪽 p-y = 홀수-홀수 = 짝수
위쪽의 해의 y값이 짝수인 경우
- 아래쪽 p-y = 홀수-짝수 = 홀수
즉, x값과, 표현하고 싶은 y값의 홀수/짝수 여부만 표현하는 것으로 타원 곡선 위의 특정 좌표를 특정할 수 있다.

동작 방식 정리

타원 곡선 위의 점(공개키)를 보내고 싶은쪽을 A, 받는쪽을 B라 하겠다.

A는 보내고 싶은 점을 구한다.
y값의 홀수/짝수 여부를 판단한다.
x와 y의 홀수/짝수여부를 직렬화하여 보낸다.
B는 x와 y의 홀수/짝수여부를 파싱한다.
이미 서로가 알고 있는 타원곡선에 x를 적용한다.
결과로 나온 두개의 y에 대해 홀수/짝수에 따라 값을 결정한다.

표현 방식

0349c4e631e3624a545de3f89f5d8684c7b81386d94bdd531d2e213bf016b278a

- y marker - 03
  - even: 02
  - odd: 03
- × - 49c4e631e3624a545de3f89f5d8684c7b81386d94bdd531d2e213bf016b278a(32 bytes)

구현

class S256Point(Point):
...
    def sec(self, compressed=True):
        '''returns the binary version of the SEC format'''
        if compressed:
            if self.y.num % 2 == 0:
                return b'\x02' + self.x.num.to_bytes(32, 'big')
            else:
                return b'\x03' + self.x.num.to_bytes(32, 'big')
        else:
            return b'\x04' + self.x.num.to_bytes(32, 'big') + \
                self.y.num.to_bytes(32, 'big')
...

결과

65byte에서 33byte로 줄어들었다.
연산량 절약과 공간 절약 두개의 측면을 비교했을 떄 비트코인의 경우 트랜잭션을 모으고, 이를 저장하는 것이 더 중요하기 때문에
공간 절약 측면이 더 영향력이 크다고 볼 수 있다.
그렇기 때문에 압축 방식을 쓰는 것이 더 좋다.

파싱 방법

보낼 때는 저렇게 보내더라도, 받는쪽에서는 결국 계산을 해야 한다.
동일 $x$ 에 대해 대칭적인 두개의 $y$ 가 나오기 때문에, 다음과 같은 수학 문제를 풀어야 한다.
$w^2 = v$

풀이 방법

\begin{aligned} w^2 & = {w^2} \cdot 1 \\ & = w^2 \cdot w^{p-1} \\ & = w^{p+1} \end{aligned}

페르마의 소정리를 사용하면 $w^2$ 은 위와 같이 정리할 수 있다.

\begin{aligned} w & = {w^{2\cdot \frac{1}{2}} } \\ & = {w^{{(p+1)}\cdot \frac{1}{2}} } \\ & = {(w^2)^{ {{(p+1)}\cdot \frac{1}{4}} } } \\ & = {v^{ {{(p+1)}\cdot \frac{1}{4}} } } \\ \end{aligned}

여기서 ${{(p+1)}\cdot \frac{1}{4}}$ 값은 무슨 값일까?
유한체에서 정의했기 때문에, 사용되는 수 역시 유한체의 특성을 만족해야 한다.
즉, 위수보다 작은 수여야 하며, 정수여야 한다.
secp256k1에서 사용하는 p는 $p\%4 = 3$ 을 만족한다.
즉, $(p+1)\%4 = 0$ 이되어 정수가 된다.

파싱 방법

보내는 방법은 알았으니, 이제 받는 방법을 알아야 한다.
위에서 계산 방법을 알았으니 코드로 적용해보자.

class S256Field(FieldElement):
...
    def sqrt(self):
        return self**((P + 1) // 4)

class S256Point(Point):
...
    @classmethod
    def parse(self, sec_bin): # SEC 바이너리를 인자로 받음
        '''returns a Point object from a SEC binary (not hex)'''
        if sec_bin[0] == 4:  # 첫 값이 4라면, 비압축임
            x = int.from_bytes(sec_bin[1:33], 'big')
            y = int.from_bytes(sec_bin[33:65], 'big')
            return S256Point(x=x, y=y)
        is_even = sec_bin[0] == 2  # 2나, 3이라면 압축방식임
        x = S256Field(int.from_bytes(sec_bin[1:], 'big'))
        # right side of the equation y^2 = x^3 + 7
        alpha = x**3 + S256Field(B) # B = 7
        # solve for left side
        beta = alpha.sqrt()  # y값을 구함
        if beta.num % 2 == 0:  #  짝수라면 홀수값도 구해줘야 함
            even_beta = beta
            odd_beta = S256Field(P - beta.num)
        else: # 홀수라면 짝수값도 구해줘야 함
            even_beta = S256Field(P - beta.num)
            odd_beta = beta
        if is_even: # 최종적으로 바이너리에서 홀/짝 요청에 따른 값을 반환함
            return S256Point(x, even_beta)
        else:
            return S256Point(x, odd_beta)