백준 - 1167 트리의 지름 (파이썬)

문제 링크 : https://www.acmicpc.net/problem/1167
난이도 : 골드 2

문제풀이

---

문제 정리

• 노드사이 거리 중 가장 긴 거리를 출력하면 된다.

분석

• 트리의 지름을 구하는 방법은 DFS나 BFS를 두번 적용하여 풀 수 있는데, 이는 귀류법을 통해 증명할 수 있다. 자세한 내용은 트리의 지름을 구하는 분석은 해당 블로그를 참고하였다.
  https://blog.myungwoo.kr/112

  • 귀류법
    어떤 명제가 참이라고 가정한 후, 모순을 이끌어내 그 가정이 거짓임을, 즉 처음의 명제가 참임을 증명하는 방법이다.

• 해당 문제에서는 가장 먼 거리의 노드를 찾고, 다시 그 노드에서 가장 먼 거리의 노드를 찾는 탐색 두번으로 가장 먼 거리에 있는 노드를 찾을 수 있다. 이는 다음과 같은 상황을 내포한다.

  • 탐색 두번은 x -> y, y -> z을 의미한다.
  • x -> z 가 트리의 지름(u -> v)인지 생각해봐야 한다.
  • 이는 4가지의 경우로 생각해 볼 수 있다.
    • x가 u와 같은 경우
    • z가 v와 같은 경우
    • x, z가 u, v와 같은 경우
    • 둘 다 같지 않은 경우

• 위에 대한 상황을 귀류법으로 증명해볼 수 있다. (참이라 가정 후 맞는지 증명)

• x, z가 u, v와 같은 경우는 다음과 같은 두 가지 상황으로 나뉜다.

  • 정점 x와 정점 y를 연결하는 경로가 정점 u와 정점 v를 연결하는 경로와 한 점 이상 공유하는 경우

  • 정점 x와 정점 y를 연결하는 경로가 정점 u와 정점 v를 연결하는 경로와 완전히 독립인 경우

    • 점 x와 정점 y를 연결하는 경로가 정점 u와 정점 v를 연결하는 경로와 한 점 이상 공유하는 경우
      
      
      
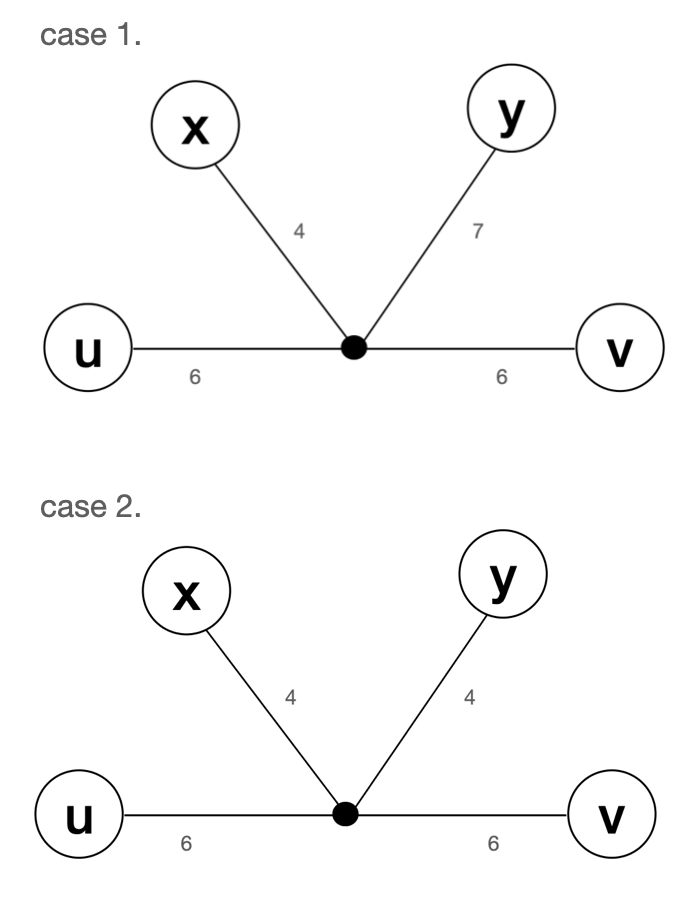
      - case1의 경우는 최대 거리가 13이고 노드는 u, y 가 되므로 트리의 지름은 u, v라는 전제에 어긋난다.
      - case2는 탐색을 두번 적용하면 최대거리가 나올 것이다.

    • 정점 x와 정점 y를 연결하는 경로가 정점 u와 정점 v를 연결하는 경로와 완전히 독립인 경우
      - x, y, u, v는 하나의 트리기 때문에 완전히 독립일 수 가 없다. 독립이면 트리의 지름은 u, v라는 전제에 어긋날 것이다.

시간복잡도

• BFS 두 번으로 인해 20만 카운트 정도 나올 것이다.

전체코드

---

from sys import stdin
from collections import deque

read = stdin.readline
N = int(input())
graph = [[] for _ in range(N+1)]

for _ in range(N):
    data = list(map(int, read().split()))
    for i in range(1, len(data) - 2 , 2):
        graph[data[0]].append([data[i], data[i+1]])

def bfs(start):
    visited = [-1] * (N+1)
    queue = deque([start])
    visited[start] = 0
    max_dist = [0,0]

    while queue:
        node = queue.popleft()

        for adj, weight in graph[node]:
            if visited[adj] == -1:
                visited[adj] = visited[node] + weight
                queue.append(adj)
                if visited[adj] > max_dist[1]:
                    max_dist = adj, visited[adj]    
    
    return max_dist

node, dist = bfs(1)
print(bfs(node)[1])

정리 및 느낀점

---

• 직관적인 아이디어에 착안하여 이를 검증할 수 있다.
• 검증 시 결론이 나올 수 있는 경우의 수에 대해 생각해 볼 필요가 있다.