[백준] (1654번) 랜선 자르기 (java)

<문제>

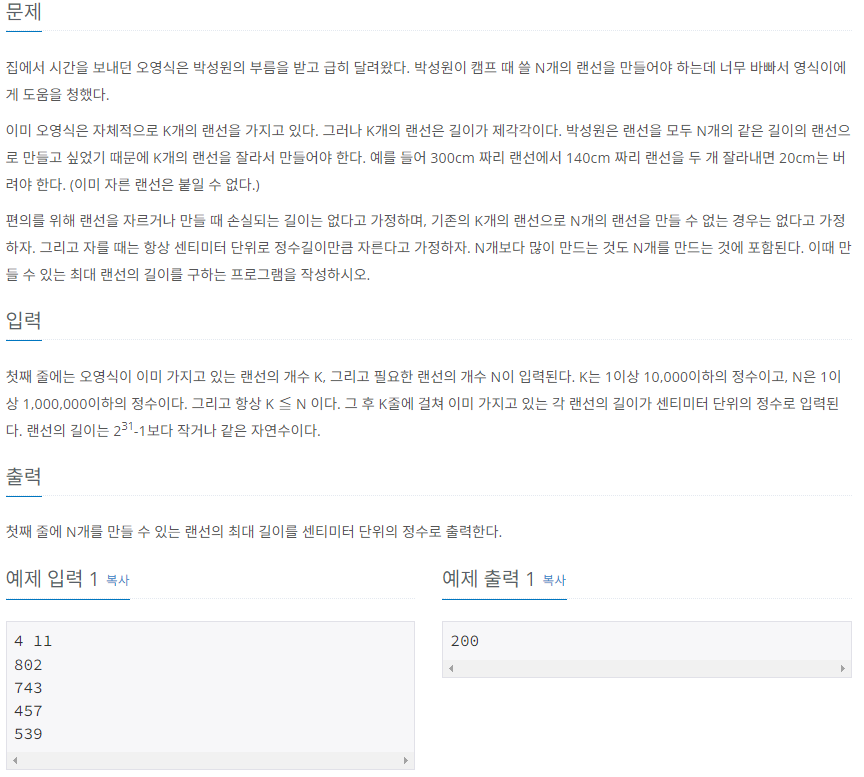
출처 : https://www.acmicpc.net/problem/1654

<나의 풀이>

import java.util.*;
import java.io.*;

public class Main {
    public static void main(String[] args)throws IOException {
		// BufferedReader로 값 받아주기. Scanner 보다 메모리를 적게 잡아먹음.
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
       
		int k = Integer.parseInt(st.nextToken());
		int n = Integer.parseInt(st.nextToken());
        
        int[] lines = new int[k];
        
        long max = 0;
        
        for (int i = 0; i < k; i++) {
            lines[i] = Integer.parseInt(br.readLine());    // 각 랜선의 길이를 받는 배열
            max = Math.max(max, lines[i]);	// 가장 큰 수를 뽑아줌.
        }
        long min = 1;    // 잘려진 랜선 길이가 자연수라 1부터 시작해야 함. 0이라 넣음 안됨.
        while (min <= max) {    // 이분탐색에 등호를 반드시 넣어야 완전하게 다 돌 수 있음.
            long mid = (min + max) / 2;
            long sum = 0;    // 2^31-1까지의 범위강 있어서 길이 합은 long형으로 지정.
            for (int line : lines) {
                sum += line / mid;
            }
            if (sum >= n) {
                min = mid + 1;
            } else {
                max = mid - 1;
            }
        }
        System.out.println(max);

    }
}

<다른 사람의 풀이>

public class Baekjoon1654 {
 
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        
        String[] firstLine = br.readLine().split(" ");
        int k = Integer.parseInt(firstLine[0]); // 가지고 있는 랜선의 개수
        int n = Integer.parseInt(firstLine[1]); // 필요한 랜선의 개수
        
        int[] inputArray = new int[k];
        for(int i=0; i<k; i++) {
            inputArray[i] = Integer.parseInt(br.readLine()); // 각 랜선의 길이 배열
        }
        Arrays.sort(inputArray);
        
        long max = inputArray[k-1]; // middle을 구하는 과정 중에 min,max 모두 int 범위를 넘을 수 있음.
        long min = 1; // 문제에서 랜선 길이는 자연수라 0으로 초기값으로 정하면 에러가 발생한다. 
        long middle = 0; // 만약 max에 int의 최대값이 들어가면 처음 middle값은 int 최대의 반인데 그 이상의 수라면 middle은 int를 넘어선다.
        
        while(max >= min) { // 이분탐색 시작
            middle = (max+min)/2;
            
            long allCount = 0;
            
            for(int j=0; j<inputArray.length; j++) {
                
                allCount += inputArray[j]/middle;
            }
            
            if(allCount >= n) { // 처음에는 ==이 되면 break를 걸어서 시간을 단축해보려고 했는데, 그건 구체적인 수를 찾을 때는 가능하지만,
                                // 문제처럼 가능한 경우의 수 중에서 최대값을 구할 경우에는 다음과 같은 부등호 처리를 해야한다.
                                // == 이 아니라도 문제에 답이 되는 경우가 존재하기 때문이다.
                
                min = middle + 1;
                
            }else if(allCount < n) {
                
                max = middle - 1;
                
            }
            
        }
        System.out.println(max);
        
    }
 
}

출처 : https://zorba91.tistory.com/56

<핵심 개념>

이분탐색은 max, min의 기준을 무엇으로 둘것인지 결정하는 것이 중요하다.
이분탐색을 더 많이 풀어보면서 max, min의 기준을 무엇으로 세울지 감을 찾는 일이 중요할 것 같다.

<피드백>

그리고 단번에 봤을 때 이분탐색인지 뭔지 모르겠으면 데이터 크기를 살펴보라는 조언을 들었다.
암튼 무지막지하게 값이 크고 (10억 이상으로 O(n)으론 절대 불가능해서 nlong(n) 사용해야 할 때 등) 최소시간, 최소 거리등의 문제가 나오면 이진탐색을 떠올리라고 한다.
그리고 이진 탐색의 풀이를 바로 떠올리기 힘들다면 파라메트릭 서치? 로 생각해보면 좋다고 하는데
파라메트릭서치 -> ~일 경우 ~인가? 에 대한 알고리즘이라고 하는데
예를 들어 k분 안에 모든 사람이 심사가 가능한가? 등의 물음에서부터 이진탐색의 기준을 찾아갈 필요가 있다고 한다.