UNIT 05 (재귀 호출)

하노이의 탑 옮기기

문제) 원반이 n개인 하노이의 탑을 옮기기 위한 원반 이동 순서를 출력하는 알고리즘을 만들어라.

# 하노이의 탑
# 입력 : 옮기려는 원반의 개수 n
# 옮길 원반이 현재 있는 출발점 기둥 from_pos
# 원반을 옮길 도착점 기둥 to_pos
# 옮기는 과정에서 사용할 보조 기둥 aux_pos
# 출력 : 원반을 옮기는 순서

def hanoi(n, from_pos, to_pos, aux_pos):
    if n == 1:
        print(from_pos, "->", to_pos)
        return

    # 원반 n-1개를 aux_pos로 이동(to_pos를 보조 기둥으로)
    hanoi(n - 1, from_pos, aux_pos, to_pos)
    # 가장 큰 원반을 목적지로 이동
    print(from_pos, "->", to_pos)
    # aux_pos에 있는 원반 n-1개를 목적지로 이동(from_pos를 보조 기둥으로)
    hanoi(n - 1, aux_pos, to_pos, from_pos)

print("n=1")
hanoi(1, 1, 3, 2)

print("n=2")
hanoi(2, 1, 3, 2)

print("n=3")
hanoi(3, 1, 3, 2)

#계산 복잡도 : O(2^n)

연습문제

5-1) 재귀 호출의 원리는 컴퓨터 그래픽에서도 많이 사용된다. 다음 그림은 모두 재귀 호출을 이용해서 만든 컴퓨터 그래픽이다.

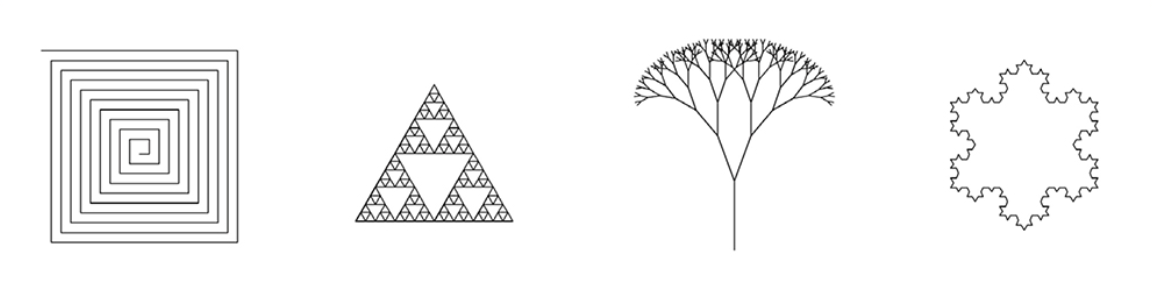
재귀 호출로 어떻게 이런 그림을 그릴 수 있을지 상상해 보고 부록 B에 있는 '재귀 호출을 이용한 그림 그리기' 부분을 읽어 봐라.

# 재귀 호출을 이용한 사각 나선 그리기
import turtle as t

def spiral(sp_len):
    if sp_len <= 5:
        return
    t.forward(sp_len)
    t.right(90)
    spiral(sp_len - 5)

t.speed(0)
spiral(200)
t.hideturtle()
t.done()

# 재귀 호출을 이용한 시에르핀스키(sierpinski)의 삼각형 그리기
import turtle as t

def tri(tri_len):
    if tri_len <= 10:
        for i in range(0, 3):
            t.forward(tri_len)
            t.left(120)
        return
    new_len = tri_len / 2
    tri(new_len)
    t.forward(new_len)
    tri(new_len)
    t.backward(new_len)
    t.left(60)
    t.forward(new_len)
    t.right(60)
    tri(new_len)
    t.left(60)
    t.backward(new_len)
    t.right(60)

t.speed(0)
tri(160)
t.hideturtle()
t.done()

# 재귀 호출을 이용한 나무 모형 그리기
import turtle as t

def tree(br_len):
    if br_len <= 5:
        return
    new_len = br_len * 0.7
    t.forward(br_len)
    t.right(20)
    tree(new_len)
    t.left(40)
    tree(new_len)
    t.right(20)
    t.backward(br_len)

t.speed(0)
t.left(90)
tree(70)
t.hideturtle()
t.done()

# 재귀 호출을 이용한 눈꽃 그리기
import turtle as t

def snow_line(snow_len):
    if snow_len <= 10:
        t.forward(snow_len)
        return
    new_len = snow_len / 3
    snow_line(new_len)
    t.left(60)
    snow_line(new_len)
    t.right(120)
    snow_line(new_len)
    t.left(60)
    snow_line(new_len)

t.speed(0)
snow_line(150)
t.right(120)
snow_line(150)
t.right(120)
snow_line(150)
t.hideturtle()
t.done()

출처

모두의 파이썬&알고리즘 합본호 / 이승찬 / 길벗 / 2018-12-10