최소 스패닝 트리

https://www.acmicpc.net/problem/1197

최소 신장 트리의 기본 문제

최소 신장 트리란

그래프에서 노드간 가중치가 최소가 되는 트리를 의미

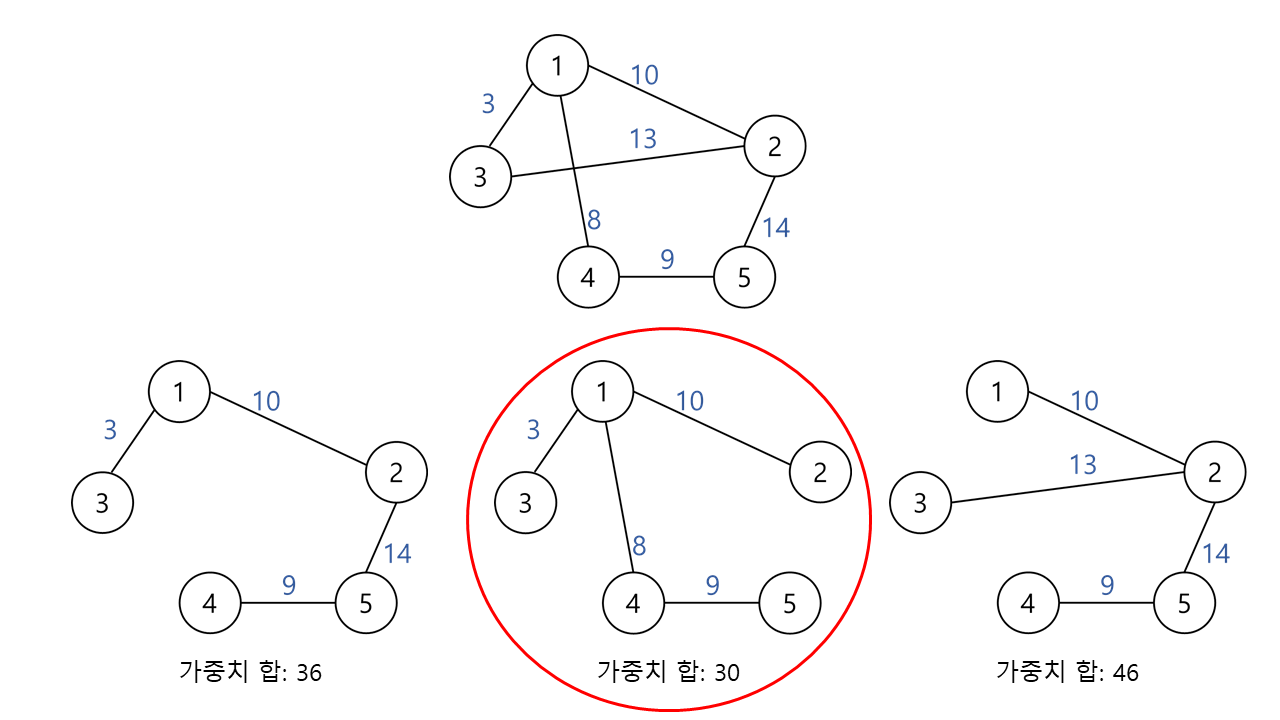
이를 해결하는 대표적인 알고리즘이 두가지 있다

• 프림 (Prim)
• 크루스카 (Kruskal)

프림 알고리즘 (Prim)

프림은 임의의 한 정점에서 시작하여 그 정점의 간선들중 가장 작은 가중치(참고로 이전 정점들의 간선들을 포함하여)의 간선을 따라가는 방식이다.

• 과정

  1. 임의의 정점을 선택하고 선택한 정점의 간선들을 가중치 올름차순 기준의 우선순위큐에 삽입
  2. 우선순위 큐에서 최우선 간선을 뽑음
     2.1 만약 뽑은 간선의 목표 정점이 방문한적이 있을 경우 넘어감
     2.2 만약 뽑은 간선의 목표 정점이 방문한적이 없을 경우 방문처리
  3. 우선순위큐가 빌때까지 2.을 반복

• 순서도
  

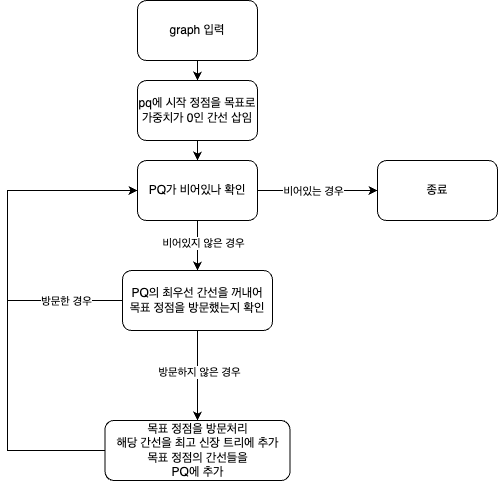
• 코드

import java.io.*;
import java.util.*;

public class Main {
    private static int V;
    private static int E;
    private static List<int[]>[] graph;
    private static boolean[] visited;
    private static int minCost;

    public static void main(final String[] args) throws IOException {
        problem(new InputStreamReader(System.in));
    }

    public static void problem(final InputStreamReader isr) throws IOException {
        init(new BufferedReader(isr));
        prim(1);
        System.out.println(minCost);
    }

    private static void init(final BufferedReader br) throws IOException {
        StringTokenizer st = new StringTokenizer(br.readLine());
        V = Integer.parseInt(st.nextToken());
        E = Integer.parseInt(st.nextToken());
        graph = new List[V+1];
        visited = new boolean[V+1];
        minCost = 0;
        for (int i = 1; i < V+1; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int i = 0; i < E; i++) {
            st = new StringTokenizer(br.readLine());
            final int start = Integer.parseInt(st.nextToken());
            final int end = Integer.parseInt(st.nextToken());
            final int weight = Integer.parseInt(st.nextToken());
            graph[start].add(new int[]{end,weight});
            graph[end].add(new int[]{start,weight});
        }
    }

    private static void prim(final int start){
        final PriorityQueue<int[]> priorityQueue = new PriorityQueue<>((o1, o2)->o1[1] - o2[1]);
        priorityQueue.add(new int[]{start,0});

        while(!priorityQueue.isEmpty()){
            final int[] edge = priorityQueue.poll();
            if (visited[edge[0]]){
                continue;
            }
            visited[edge[0]] = true;
            minCost += edge[1];
            for (final int[] nextEdge : graph[edge[0]]){
                priorityQueue.add(nextEdge);
            }
        }
    }
}

크루스카 알고리즘 (Kruskal)

모든 간선을 가중치를 오름차순 기준으로 정렬한 후 사이클이 형성하지 않은 간선들을 추가해나가는 방식

• Union&find 자료구조
  • 서로소(Disjoint Set)을 표현하는 자료구조
  • 노드가 바라보는 최상위 노드가 같은 노드인지 확인
  • find : 노드의 최상위 노드를 확인
  • Union : 한 노드를 다른 노드를 바라보게 하여 해당 노드가 다른 노듣의 집합에 포함되게 함
• 과정
  1. 모든 간선을 가중치의 오름차순으로 정렬
  2. 정렬된 간선을 순차적으로 방문
     2.1 방문한 간선의 출발 정점과 도착 정점이 서로소인 경우, 간선을 최고 신장 트리에 포함, 출발 정점과 도착 정점을 Union
     2.2 방문한 간선의 출발 정점과 도착 정점이 서로소가 아닌 경우, 무시하고 다른 간선 방문 제게
• 순서도
  
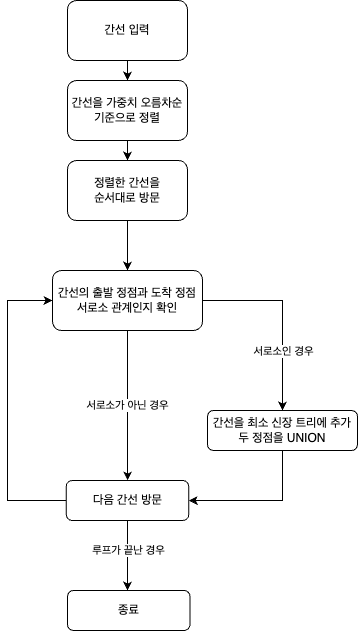
• 코드

import java.io.*;
import java.util.*;

public class Main {
    private static int V;
    private static int E;
    private static int[][] graph;
    private static int[] parent;
    private static int minCost;

    public static void main(final String[] args) throws IOException {
        problem(new InputStreamReader(System.in));
    }

    public static void problem(final InputStreamReader isr) throws IOException {
        final BufferedReader br = new BufferedReader(isr);
        StringTokenizer st = new StringTokenizer(br.readLine());
        V = Integer.parseInt(st.nextToken());
        E = Integer.parseInt(st.nextToken());
        minCost = 0;
        graph = new int[E][3];
        parent = new int[V+1];
        for (int i = 1; i < V+1; i++) {
            parent[i] = i;
        }
        for (int i = 0; i < E; i++) {
            st = new StringTokenizer(br.readLine());
            graph[i][0] = Integer.parseInt(st.nextToken());
            graph[i][1] = Integer.parseInt(st.nextToken());
            graph[i][2] = Integer.parseInt(st.nextToken());
        }
        Arrays.sort(graph, (o1,o2) -> o1[2] - o2[2]);
        for (int i = 0; i < E; i++) {
            kruskal(i);
        }
        System.out.println(minCost);
    }

    private static void kruskal(final int v){
        if (find(graph[v][0]) != find(graph[v][1])){
            union(graph[v][0],graph[v][1]);
            minCost += graph[v][2];
        }
    }

    private static void union(final int a, final int b){
        final int aParent = find(a);
        final int bParent = find(b);
        if (aParent > bParent){
            parent[aParent] = bParent;
            return;
        }
        parent[bParent] = aParent;
    }

    private static int find(final int x){
        if (parent[x] == x){
            return x;
        }
        parent[x] = find(parent[x]);
        return parent[x];
    }
}