Tools

이 글에서는 통계학 및 딥러닝/머신러닝 분야에서 많이 사용되는 수학적 도구들을 정리하고자 한다.

---

공돌이의 수학노트님의 블로그들을 통해 많은 지식을 얻었으며 아래 정리 또한 많이 참고했음을 알린다. 좋은 자료 공유해주셔서 감사합니다.

공돌이의 수학노트: https://angeloyeo.github.io

---

1. Entropy

엔트로피는 확률분포가 지닌 불확실성, 즉 평균 정보량을 나타내는 지표이다. 엔트로피는 여러 방식으로 표기할 수 있으며, 대표적인 세 가지 표현은 다음과 같다.

• 이산형 확률분포:

  $H(X) = -\sum_{x \in X} p(x) \log p(x)$

• 연속형 확률분포:

  $H(X) = -\int_{x \in X} p(x) \log p(x) \, dx$

• 기댓값 표기법:

  $H(X) = -\mathbb{E}_{p}[\log p(x)]$

엔트로피가 높을수록 해당 분포는 불확실성이 크고, 반대로 낮을수록 결정성이 높다고 할 수 있다. 예를 들어, 모든 면이 동일한 확률로 나오는 공정한 주사위의 엔트로피는, 특정 면(예: 2)의 확률이 1/2이고 나머지 면의 확률이 1/10인 편향된 주사위의 엔트로피보다 높다.

2. Cross Entropy

크로스 엔트로피는 실제 분포 (P)와 모델 분포 (Q) 사이의 차이를 측정하는 지표로, 실제 분포로부터 샘플링된 데이터를 모델 분포로 인코딩할 때 필요한 평균 정보량을 나타낸다. 역시 다양한 방식으로 표현할 수 있다.

• 이산형 확률분포:

  $CE(P, Q) = -\sum_{x \in X} P(x) \log Q(x)$

• 연속형 확률분포:

  $CE(P, Q) = -\int_{x \in X} P(x) \log Q(x) \, dx$

• 기댓값 표기법:

  $CE(P, Q) = -\mathbb{E}_{P}[\log Q(x)]$

두 분포가 완전히 일치할 경우 크로스 엔트로피는 엔트로피와 동일한 값을 가지며, 분포 차이가 클수록 그 값은 더 커진다.

3. Kullback-Leibler Divergence

쿨백-라이블러 발산(또는 KL 발산)은 두 확률분포 (P)와 (Q) 사이의 차이를 측정하는 도구이다. 이는 실제 분포 (P)를 모델 분포 (Q)로 근사할 때 발생하는 추가 정보량, 즉 부정확한 근사로 인한 추가 코드 길이를 의미한다.

• 이산형 확률분포:

  $D_{KL}(P \parallel Q) = \sum_{x \in X} P(x) \log \frac{P(x)}{Q(x)}$

• 연속형 확률분포:

  $D_{KL}(P \parallel Q) = \int_{x \in X} P(x) \log \frac{P(x)}{Q(x)} \, dx$

쿨백-라이블러 발산은 항상 0 이상의 값을 가지며, (P)와 (Q)가 완전히 동일할 경우 $D_{KL}(P \parallel Q) = 0$ 이 된다.

또한, 크로스 엔트로피는 엔트로피와 쿨백-라이블러 발산의 합으로 나타낼 수 있다:

이를 통해 모델 분포 (Q)가 실제 분포 (P)를 얼마나 잘 근사하는지 평가할 수 있으며, 근사 오차가 줄어들수록 크로스 엔트로피는 엔트로피에 가까워진다.

4. Bayes' Theorem

베이지안 정리는 주어진 조건 하에서 사건의 확률을 갱신하는 방법을 제공한다. 베이지안 정리는 다음과 같이 정의된다.

생성형 네트워크에서 추론 과정을 거칠때 필수적으로 들어가는 요소이다.

5. MLE

Maximum Likelihood Estimate란 관측된 데이터를 가장 그럴싸하게(확률적으로) 만들어냈을 것으로 추정되는 파라미터를 찾는 방법이다. 여기서 우도란, 가정한 분포하에서 관측된 데이터가 나올 가능도를 말한다.

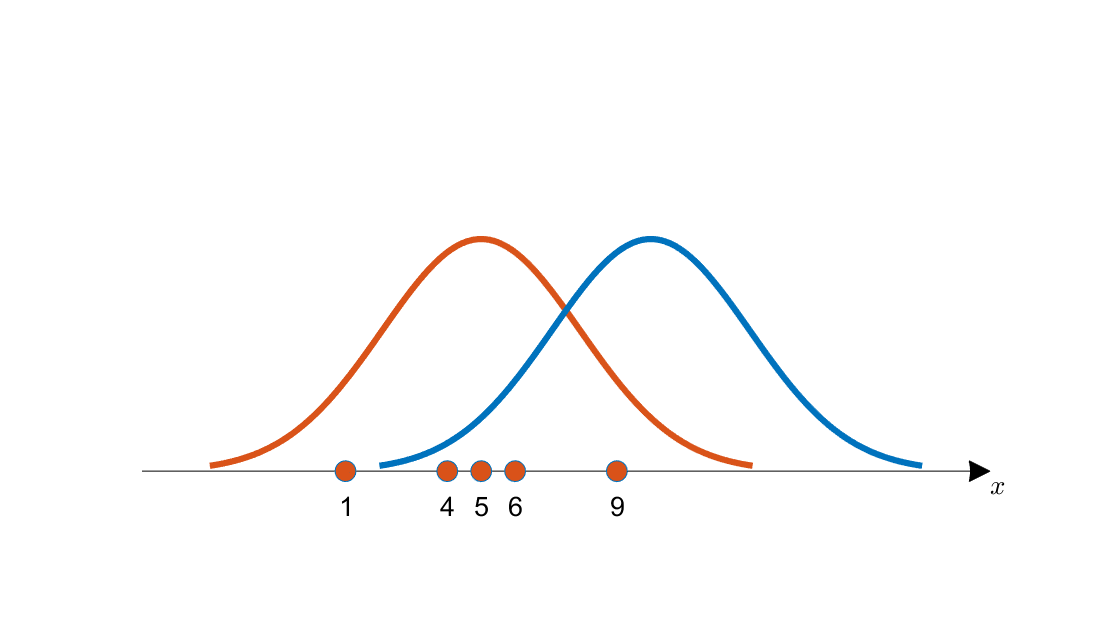
다음과 같이 관측된 데이터를 $x= [1,4,5,6,9]$ 라고 하자. 그리고 이를 생성했을 법한 후보 분포(오렌지색과 파란색)가 두 가지 있다고 가정하자.

관측된 데이터가 4, 5, 6에 많이 몰려 있음을 직관적으로 확인할 수 있다. 따라서 이 데이터를 생성했을 분포가 어느 쪽인지 직관적으로는 오렌지색 분포가 더 그럴싸해 보인다.

전체 가능도(우도)를 구하는 방법은 다음과 같다. 이때 각 데이터 포인트는 $iid$ 를 가정한다.

다시 MLE로 돌아와서 이제 파라미터 추정을 해보자.

위의 $L(\theta)$ 형태에서는 연산이 힘드므로 $log$ 연산을 통해 $product$ 연산을 빼자.

이제 위 $l(\theta)$를 미분 연산하여 가장 기여도를 크게 만드는 $\theta$를 추정하자.

위 과정을 최대우도추정법 MLE라고 한다.

6. MAP