UIBezierPath

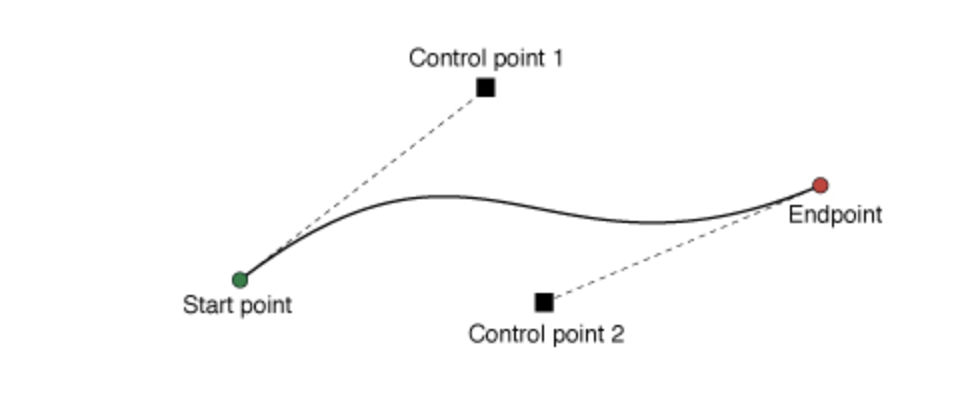
• 코드로 그림도 그리고 이미지를 원하는 모양으로 클리핑하는것들이 가능한 BezierPath.
• 근데일단. 나는 베지어곡선이 뭔지 모름.

베지어곡선?

• 특정한 기준점을 중심으로 그려지는 매끄러운 곡선그래프

1차 베지어곡선

• 두 점을 잇는 직선
• 식으로 나타내면 아래와 같다.

P=t * P_1+(1-t)P_2
// t는 0 부터 1까지의 모든 실수
//모든 t에 대한 자취가 바로 베지어곡선

ex) p_1 가 (0,100) p_2가 (100, 0)인 경우의 자취점을 대강 찾아보면
1) t가 0 : P = 0 >> (100,0)
2) t가 0.1 : P = 0.1 (0,100) + 0.9 (100, 0) >> (90, 10)
3) t가 0.2 : P = 0.2 (0,100) + 0.8 (100, 0) >> (80, 20)
4) ...
n) t가 1 : P = 1 (0,100) + 0 (100, 0) >> (100, 100)

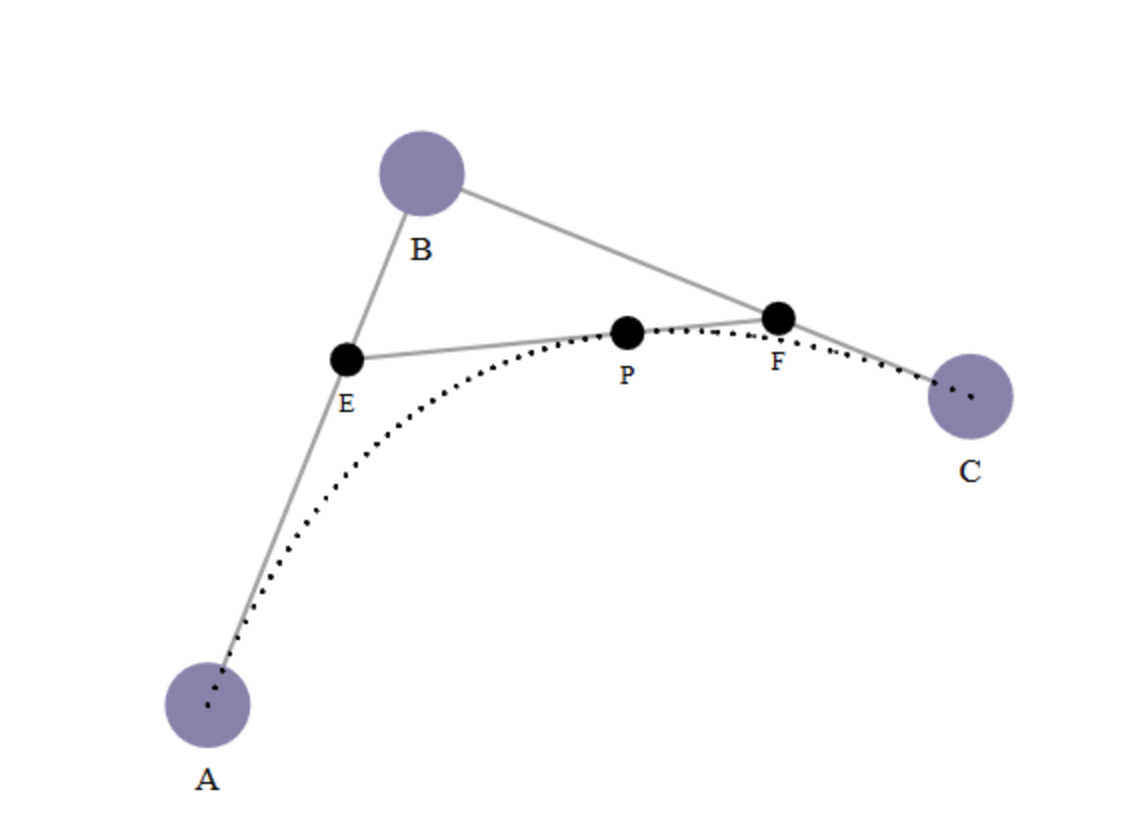
2차 베지어곡선

• 2차 베지어 곡선은 3개의 기준점을 통해 그리기를 완성한다.
• 직선 AB와 직선 BC위에 내분점 E, F가 만들어지는데
• 이때, E와 F사이에 점 P가 천천히 돌아가는 방향으로 발생한다.

P(t) = (1-t){(1-t)A + tB} + t{(1-t)B+tC}

ex) A(0, 100), B(50, 0), C(100, 50) 인경우의 곡선을 그려보면

1) t가 0
P(0) = A (0, 100)
2) t가 0.1
P(0.1) = 0.9(0.9A + 0.1 B) + 0.1(0.9B + 0.1C)
= 0.81A + 0.09B + 0.09B + 0.01C
= (0, 81) + (9,0) + (1, 0.5)
= (10, 81.5)
3) t가 0.2
P(0.2) = 0.8(0.8A + 0.2 B) + 0.2(0.8B + 0.2C)
= 0.64A + 0.16B + 0.16B + 0.04C
= (0, 64) + (16,0) + (4, 2)
= (20, 66)
5) t가 0.3
P(0.3) = 0.7(0.7A + 0.3 B) + 0.3(0.7B + 0.3C)
= 0.49A + 0.21B + 0.21B + 0.09C
= (0, 49) + (21,0) + (9, 4.5)
= (30, 53.5)
…
P(1) = C
= (100, 50)

• ABC지점만 보고 어떤 수치로 그려질지 바로 떠오르진 않겠지만 t가 증가할수록 점p 가 b,c와 가까워진다는거랑 b쪽으로 곡선이 치우쳐져 그려질것이라는 정도는 추측이 가능할거같다.

  3차 베지어곡선

• 3차 베지어 곡선은 4개의 기준점을 통해 그리기를 완성한다.

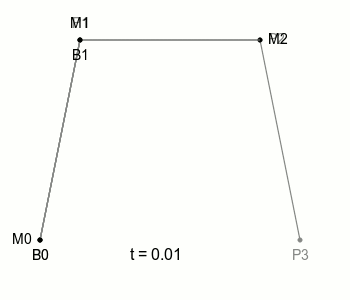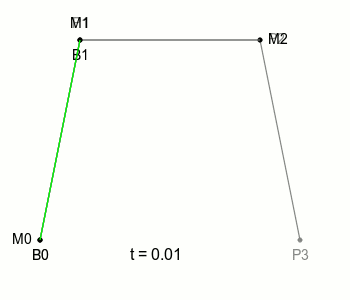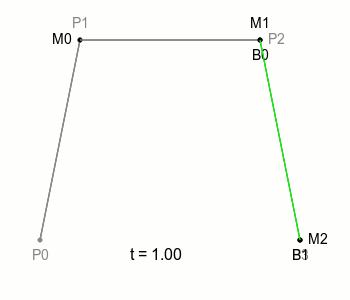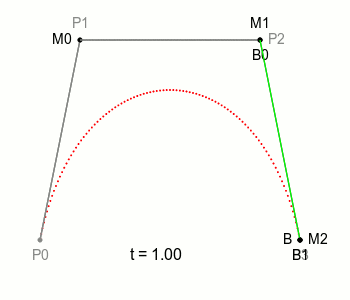
• 예시로가져온 아래 그림을 보면

• P0P1직선 P1P2직선 P2P3직선을 지나는 M0, M1, M2(세점은 같은 속도로 이동한다.)의 내분점 B0, B1(두점도 같은속도로 이동)로 그어진 직선의 내분점 B를 이용해 그려진 곡선을 확인할 수 있다.
  
  참고 : https://blog.coderifleman.com/2016/12/30/bezier-curves/index.html

UIBezierPath

• 곡선과 직선을 조합하는 세그먼트들로 구성된 Path들로, 커스텀한 view를 보여줄수 있다. (직사각형, 타원, 호, 글리프(도형 기호)와 같은 모양을 그릴 수있다.)
• 하나의 Path는 두 끝점을 연결하여 단일 경로를 close하거나 open된 상태로도 둘 수있다.

UIBezierPath객체

• NSBezierPath 객체는 disconnected된 여러개의 path들을 갖는다. (여기서 path는 closed거나 open이거나 무관)
• 각 path들을 subPath라고 부른다.
• Bézier path object의 subpaths는 그룹으로 컨트롤되어야한다.
• subpaths를 개별로 조작할수 있는 방법은 NSBezierPath objects를 새로 생성하는 방법뿐이 없다.
• NSBezierPath 객체로 path의 outline을 잡거나 path에 의해 잡힌 영역을 채울수도 있다.
• path를 view나 다른 영역의 clipping영역으로 사용할 수도 있다.
• NSBezierPath의 method를 사용해서 filled되어있거나 strock(선부분)되어있는 곳의 hit감지를 할수도있다(영역터치/드래깅 등)

몇가지 메소드들

func move(to point: CGPoint)

• path의 현재 포인트를 특정 location으로 이동시켜준다.
• 진행중인 subpath를 닫고 파라미터로 들어온 포인트를 현재 포인트로 설정한다.
• 곡선이나 세그먼트 그리는 명령하기 전에 꼭 이메서드를 호출해야한다.
  path

func addLine(to point: CGPoint)

• path에 직선 긋기
• point : 직선의 도착지점
• method사용하기 전에 move(to:) 를 이용해서 path의 현재 point를 세팅해줘야한다.

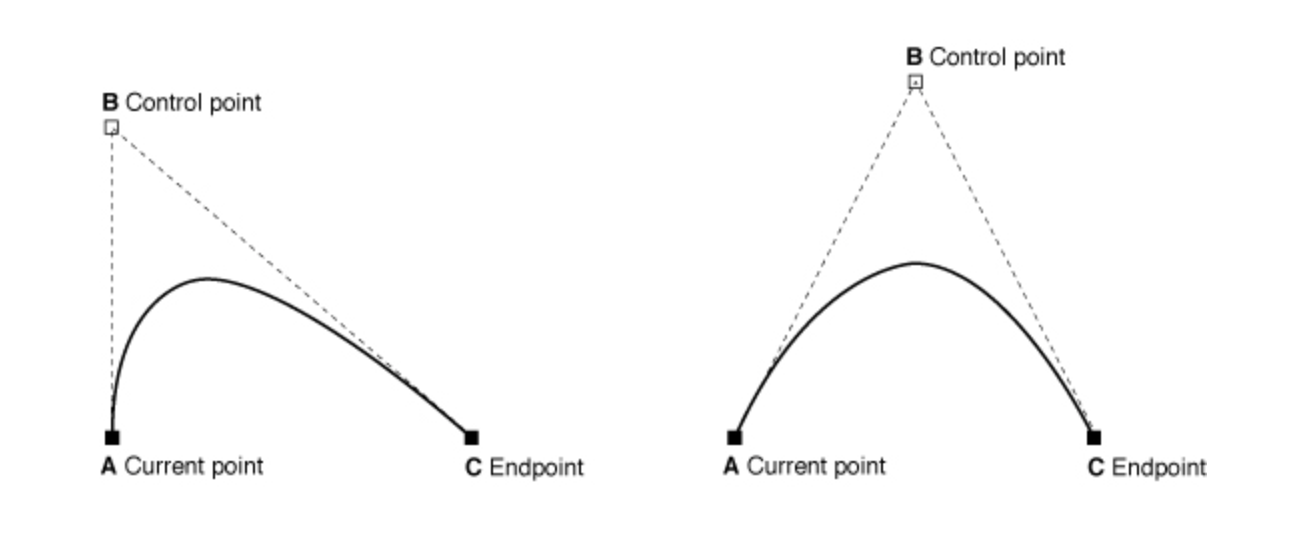
func addQuadCurve(to endPoint: CGPoint, 
     controlPoint: CGPoint)

• path에 2차 베지어곡선을 추가한다.
• endPoint : 곡선의 end 지점
• controlPoint: 곡선의 control point
• method사용하기 전에 move(to:) 를 이용해서 path의 현재 point를 세팅해줘야한다.
  

func addCurve(to endPoint: CGPoint, 
controlPoint1: CGPoint, 
controlPoint2: CGPoint)

• path에 3차 곡선을 추가한다.
• aPoint: curve segment의 목적 point
• controlPoint1: 현재 포인트에서 가까운쪽의 curve모양
• controlPoint2: destination 포인트에 가까운쪽에서의 curve모양
• method사용하기 전에 move(to:) 를 이용해서 path의 현재 point를 세팅해줘야한다.