
Chapter 3. 연산자
10. 산술 변환
- 연산 전에 피연산자 타입의 일치를 위해 자동 형변환되는 것은 이항 연산자에서만 아니라 단항 연산에서도 일어남
🍕 규칙
① 두 피연산자의 타입을 같게 일치 시킴(보다 큰 타입으로 일치)
▶ 피연산자의 값손실을 최소화하기 위한 것
long + int → long + long → long
float + int → float + float → float
double + float → double + double → double
② 피연산자의 타입이 int보다 작은 타입이면 int로 변환
▶ 타입의 표현범위가 좁아서 연산 중에 오버플로우(overflow) 발생 가능성이 높기 때문
byte + short → int + int → int
char + short → int + int → int
- 연산결과의 타입은 피연산자와의 타입과 일치
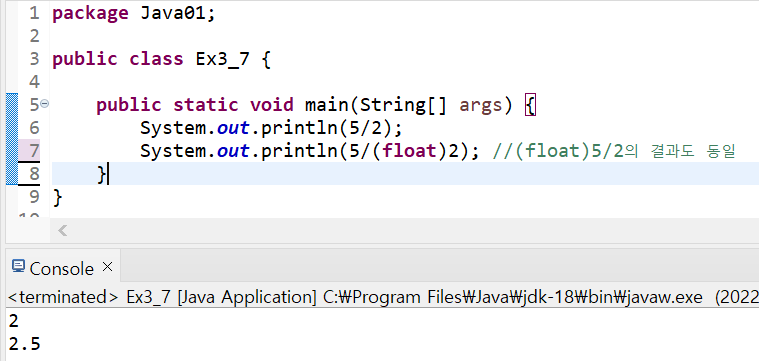
▶ 예를들어 int와 int의 나눗셈 연산결과는 int
byte a = 10;
byte b = 20;
byte c = a + b; ▶컴파일하면 에러 발생.
System.out.println(c);
▶ a와 b는 모두 int형보다 작은 byte형이기 때문에 연산자 '+'는 두개의 피연산자들의 자료형을
int형으로 변환한 다음 연산을 수행
: byte c = (byte)(a+b); 로 변환
▶ 그래서 'a+b'의 연산결과는 byte형(1byte)이 아닌 int형(4byte)임- 크기가 작은 자료형의 변수를 큰 자료형의 변수에 저장할 때는 자동으로 형변환(typeconversion, casting)되지만, 큰자료형의 값을 작은 자료형의 변수에 저장하면 명시적 형변환 연산자를 사용하여 변환필요
-
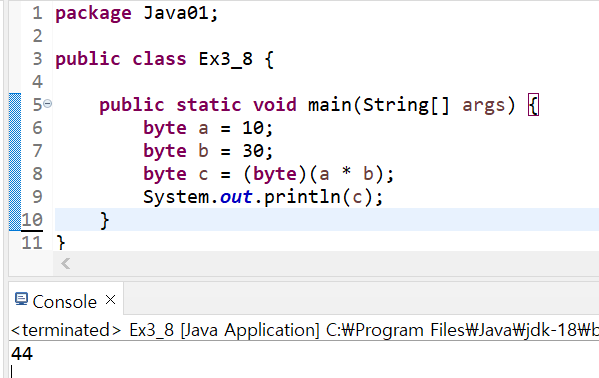
위 예제를 실행하면 44가 출력. '10 * 30'의 결과는 300이지만, 큰 자료형에서 작은 자료형으로 형변환(캐스팅,casting)하면 데이터의 손실이 발생하므로 값이 변경될 수 있음. 즉, 300은 byte형의 범위를 넘기 때문에 byte형으로 변환하면 데이터 손실이 발생
✅byte → int: 값손실 없음
✅int → byte: 값손실 있음
-
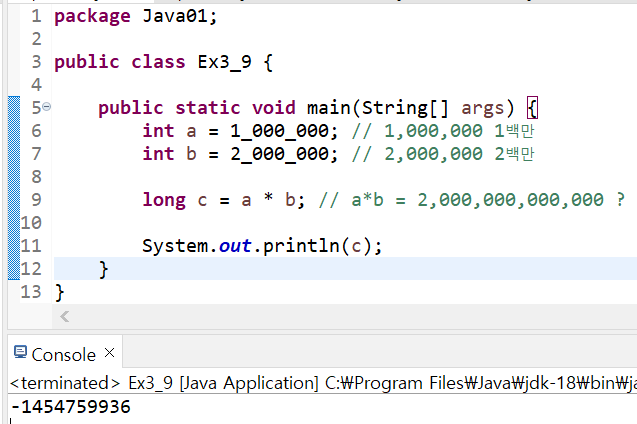
식 'a * b'의 결과 값을 담는 변수 c의 자료형이 long타입(8byte)이지만, int타입과 int타입의 연산결과는 int타입이기 때문에 결과는 int타입의 값(-1434759936)이므로 long형으로 자동 형변환되어도 값은 변하지 않음
▶올바른 결과를 얻기 위해서 변수 a 또는 b타입을 'long'으로 형변환 필요
long c = (long)a * b;
long c = (long)1000000 * 2000000;
long c = 1000000L * 2000000;
long c = 1000000L * 2000000L;
long c = 2000000000000L;
1000000(int)*1000000(int) → -727379968(int) 오버플로우 발생!
1000000(int)*100000L(long) → 1000000L(long)*1000000L(long) → 1000000000000L(long)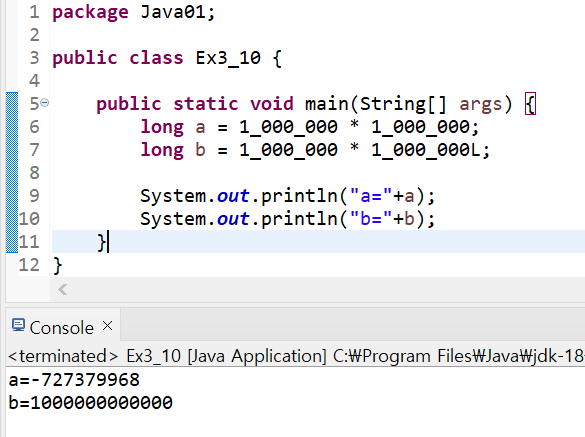
11. Math.round()로 반올림하기
Math.round(): 반올림 메서드. 소수점 첫째 자리에서 반올림한 결과를 정수로 변환
▶ long result = Math.round(4.52); //result에 5저장- 만일 소수점 첫째 자리가 아닌 다른 자리에서 반올림하려면 10의 n제곱으로 적절히 곱하고 나누어야 함
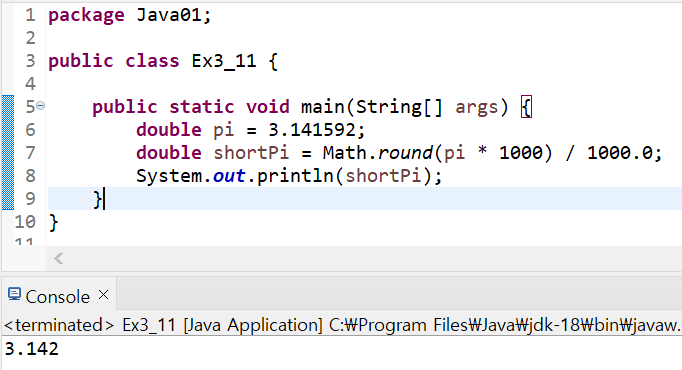
Math.round(pi*1000) / 1000.0
→ Math.round(3.141592 * 1000) / 1000.0
→ Math.round(3141.592) / 1000.0
→ 3142 / 1000.0(double) (*)
→ 3.142
(*)위 과정에서 1000.0이 아니라 1000으로 나누었으면 결과는 3.142가 아닌 3이 됨. int와 int의 나눗셈 결과는 int이기 때문
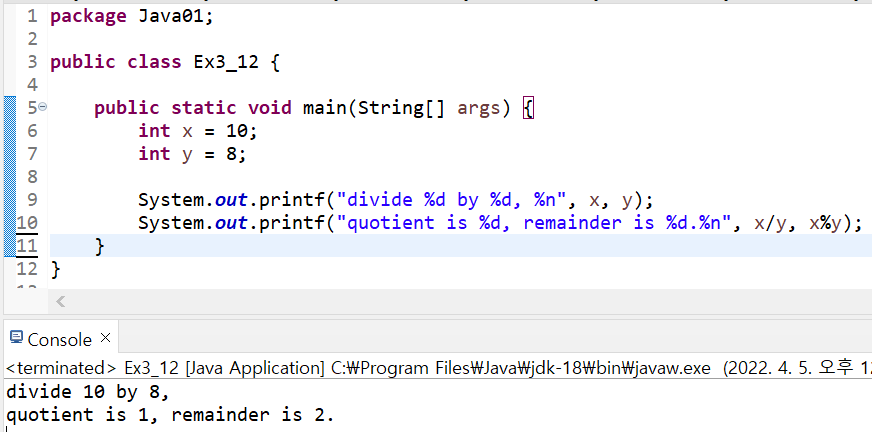
12. 나머지 연산자
-
나머지 연산자: 왼쪽의 피연산자를 오른쪽 피연산자로 나누고 난 나머지 값을 결과로 반환 -
나누는 수(오른쪽 피연산자)로 0 사용 불가
-
피연산자로 정수와 실수 허용
-
주로 짝수, 홀수 또는 배수 검사 등에 사용
-
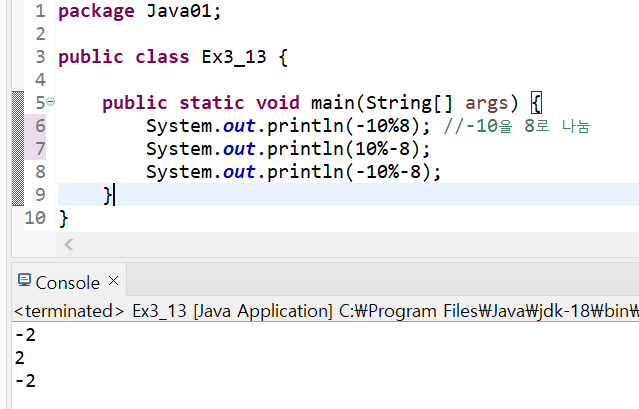
나머지 연산자(%)는 나누는 수로 음수도 허용. 그러나 부호는 무시되므로 결과는 음수의 절대값으로 나눈 나머지와 결과가 같음
-
피연산자의 부호를 모두 무시하고, 나머지 연산을 한 결과에 왼쪽 피연산자(나눠지는 수)의 부호를 붙이면 됨
