세그먼트 트리(Segment Tree)

• 여러 개의 데이터가 존재할 때 특정 구간의 합(최솟값, 최댓값, 곱 등)을 구하는 데 사용하는 자료구조입니다.
• 트리 종류 중에 하나로 이진 트리의 형태이며, 특정 구간의 합을 가장 빠르게 구할 수 있다는 장점이 있습니다. 시간복잡도 : O(logN)

단순히 반복문을 활용하여 구간합을 구할 경우, 시간복잡도는 O(N) 입니다.
하지만, 세그먼트 트리는 O(logN)이므로 단순히 N이 1억인 케이스만 비교해도 세그먼트 트리는 최악의 경우 약 27번 정도의 검색으로 합을 구할 수 있게 됩니다.

세그먼트 트리 구현하기

세그먼트 트리 공간 만들기

세그먼트 트리는 완전 이진트리(Full Binary Tree)입니다.
따라서 크기가 N인 배열을 세그먼트 트리를 만들 때는 다음과 같은 노드의 수가 필요합니다.

세그먼트 트리는 가장 마지막 노드가 단일원소의 합이므로 리프노드의 갯수가 N인 트리가 됩니다.

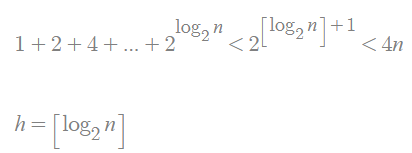
위의 공식에 의해 높이가 h라면 필요한 배열의 크기는 2^(h+1) - 1이며 편의를 위해 2^(h+1) 또는 4n으로 크기를 정하게 됩니다.

이제 예제와 함께 시작해보겠습니다.

arr = [1,2,3,4,5,6,7,8,9,10]
tree = [0] * (len(arr)*4)

arr의 크기는 10이고, 저는 쉽게 계산하기 위해서 len(arr)*4(4n) 정도의 크기로 생성하겠습니다.

세그먼트 트리 초기화하기

먼저 루트노드에는 모든 구간합이 담기고, 루트노트의 자식노드는 각 구간을 반으로 나눈 값이 저장됩니다. (루트노드 0~9, 루트노드의 자식노드 0~4, 5~9)

그리고 이걸 자식노드까지 계속 적용하면 아래와 같은 형태가 됩니다.

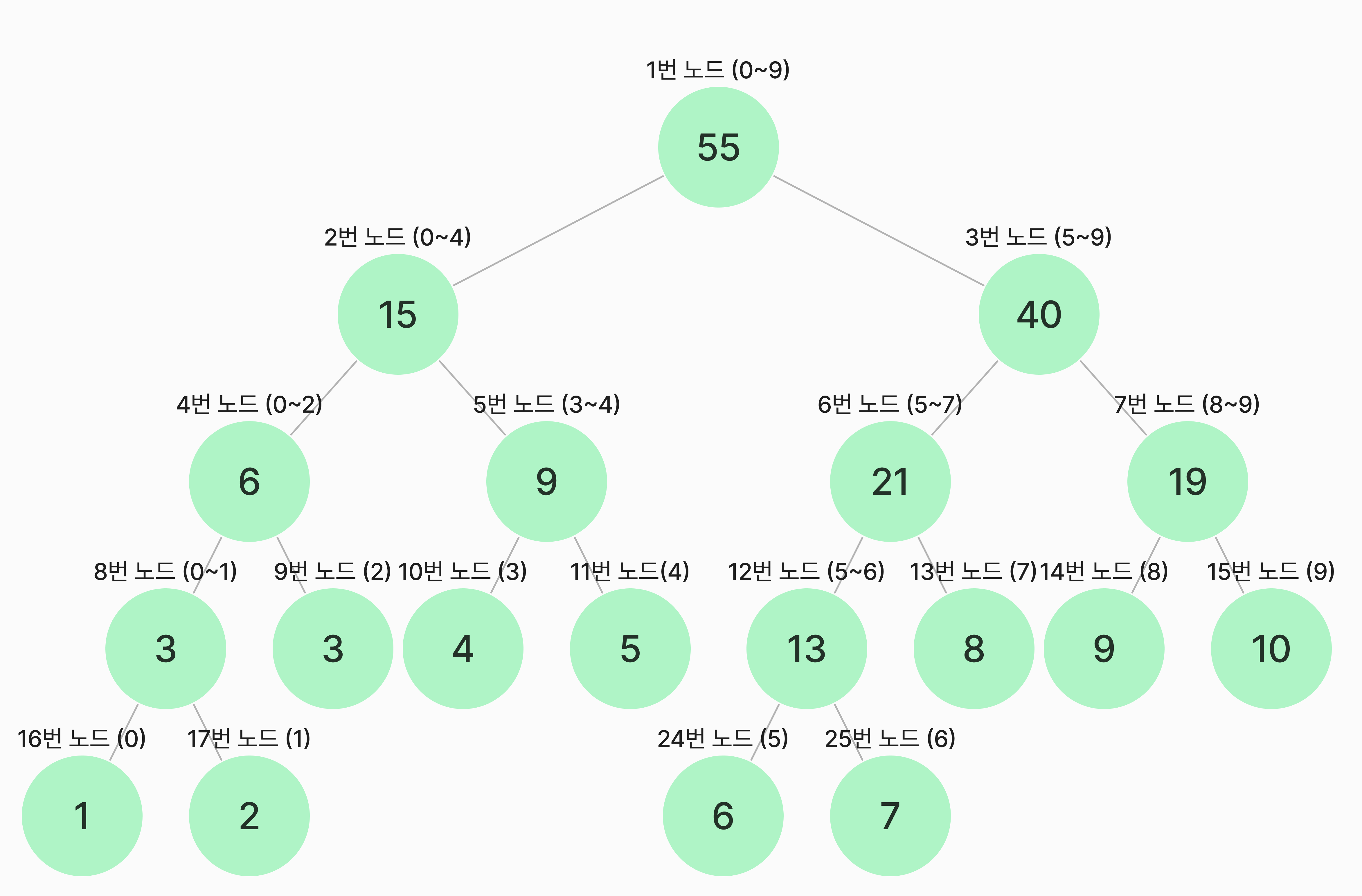
세그먼트 트리는 각 노드가 이미 특정 구간의 합을 가지고 있는 형태가 됩니다. 저는 세그먼트 트리가 하나만 존재하니 함수인자에 미리 초기값을 지정했습니다.

node가 1부터 시작하는 이유?
> 노드값이 1부터 시작해야 부모노드의 자식노드를 계산하기가 쉽기 때문입니다.

arr = [1,2,3,4,5,6,7,8,9,10]
tree = [0] * (len(arr)*4)

def init(left_node=0, right_node=len(arr)-1, node=1):
    if left_node == right_node:
        tree[node] = arr[left_node]
        return tree[node]
    mid = (left_node+right_node)//2
    tree[node] = init(left_node, mid, node*2) + init(mid+1, right_node, node*2+1)
    return tree[node]
    
init()
print(tree)
# [0, 55, 15, 40, 6, 9, 21, 19, 3, 3, 4, 5, 13, 8, 9, 10, 1, 2, 0, 0, 0, 0, 0, 0, 6, 7, 0, 0, ...]

세그먼트 트리를 구축할 때는 시간복잡도가 O(NlogN)입니다. 그렇다면, 구간합(ex. PrefixSum) 방식으로 구현하는게 더 빠른게 아닐까? 할 수 있습니다. 실제로 구간합을 위해서 미리 계산할 땐 O(N)의 시간복잡도 밖에 되지 않습니다.

하지만 세그먼트 트리의 장점은 중간에 데이터가 변경되는 경우에 있습니다.
데이터 변경이 생기면 구간합은 O(N)의 시간복잡도가 필요하지만 세그먼트 트리는 구축할 때만 O(NlogN)일 뿐, 합을 구하거나 데이터변경이 생긴다고 해도 O(logN)의 시간복잡도만 가집니다.

세그먼트 트리를 활용하여 구간합 구하기

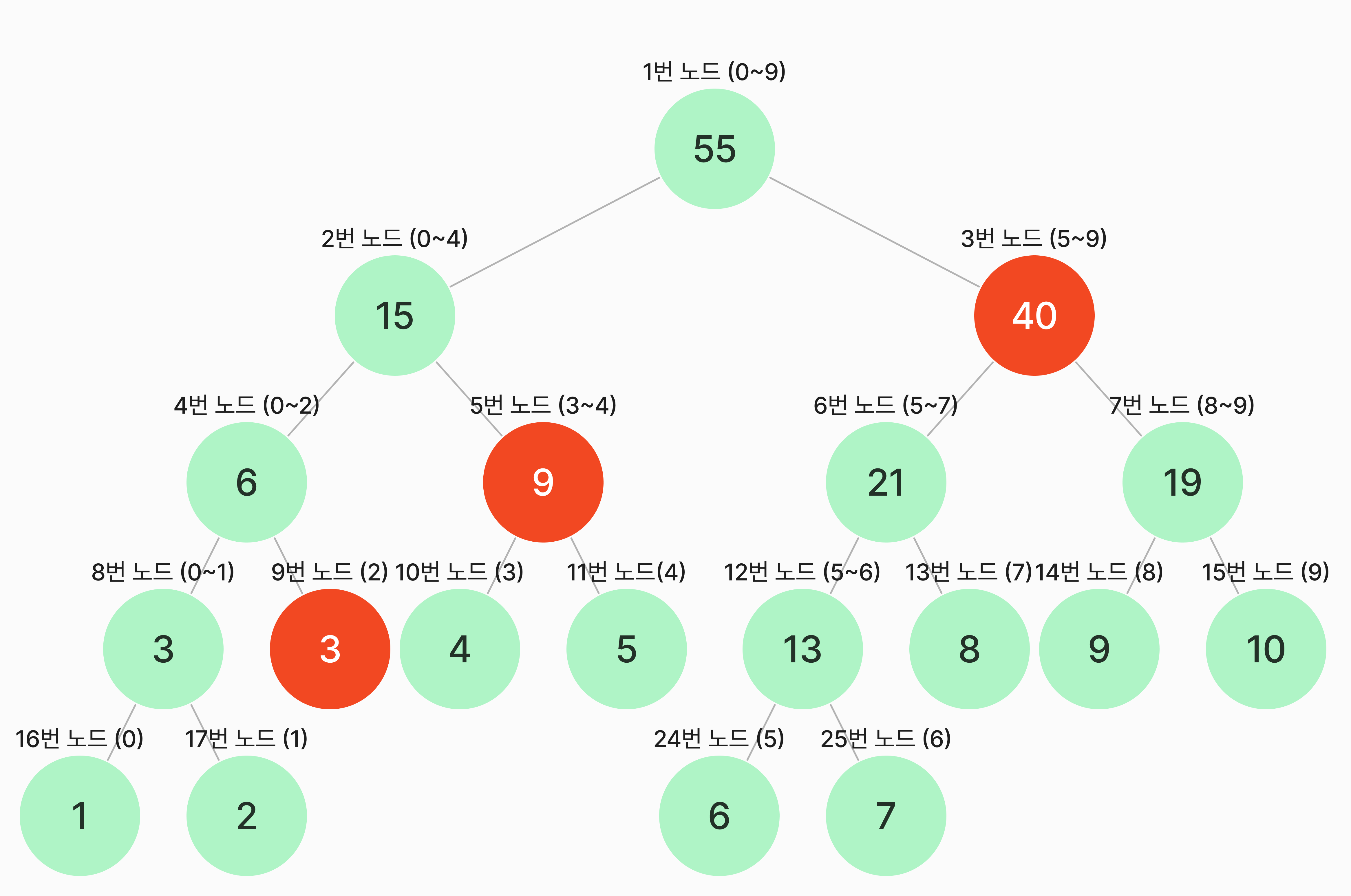
arr를 기준으로 index 2에서부터 9까지의 합을 구하고자 할때 반복문을 사용한다면 arr[2]+arr[3]+arr[4]+... + arr[9] = 52를 얻을 수 있습니다. 이제 세그먼트 트리를 활용했을 때 어떻게 log2(N)의 시간복잡도가 나오는지 확인해봅시다.

먼저, 이미지 상으로 확인했을 때 2~9까지의 구간합은 9번 노드, 5번 노드, 3번 노드를 합한 값이 됩니다.

call_def = 0

def segment_sum(start, end, left_node=0, right_node=len(arr)-1, node=1):
    global call_def
    call_def += 1
    # 범위 밖에 있는 경우
    if start > right_node or end < left_node:
        return 0
    # 범위 안에 있는 경우
    if start <= left_node and right_node <= end:
        print(f"구간 {left_node}~{right_node} : {tree[node]}")
        return tree[node]
    mid = (left_node+right_node)//2
    return segment_sum(start, end, left_node, mid, node*2) + segment_sum(start, end, mid+1, right_node, node*2+1)
    
res = segment_sum(2, 9)
# 구간 2~2 : 3
# 구간 3~4 : 9
# 구간 5~9 : 40
print(f"합은 {res}, 함수는 {call_def}번 호출되었습니다.")
# 합은 52, 함수는 7번 호출되었습니다.

이번에도 편의를 위해 함수인자에 초기값을 미리 저장해뒀습니다.
디버그를 위해 넣어둔 print문을 확인해보면, 총 3번의 합으로 2~9까지의 구간합을 계산했습니다.

특정 원소의 값 변경

세그먼트 트리는 미리 구간 합을 계산해놓기 때문에 데이터의 값이 변경될 경우, 영향을 받는 구간은 모두 다시 합을 계산해야 합니다.

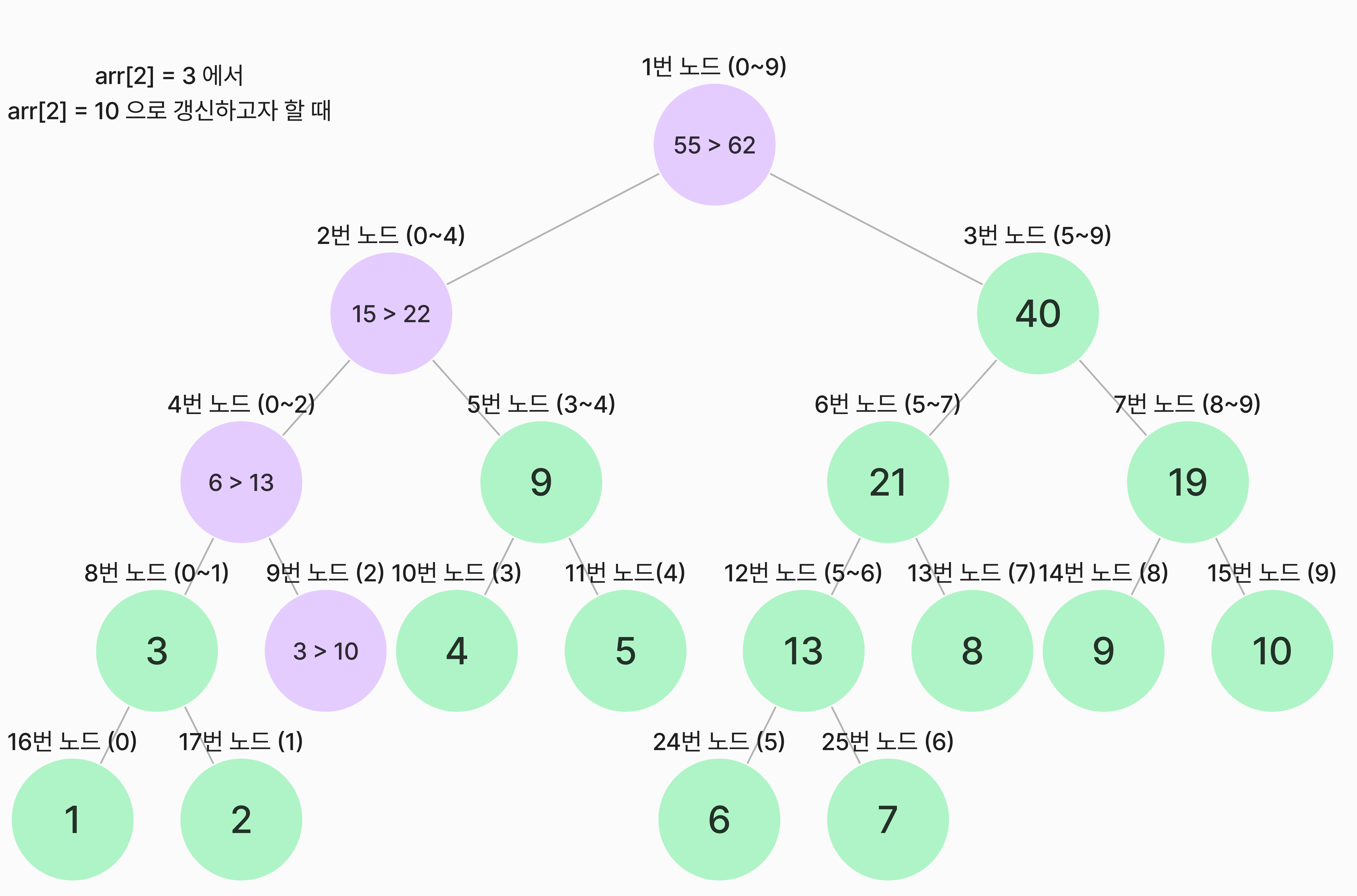
arr에서 index 2번의 원소를 3에서 10으로 변경하고자 할 때 세그먼트 트리에서는 위의 이미지와 같은 갱신이 이루어져야 합니다.

def update(index, value, left_node=0, right_node=len(arr)-1, node=1):
    if index < left_node or index > right_node:
        return
    # 범위 안에 있으면
    tree[node] += value-arr[index]
    if left_node == right_node:
        return
    mid = (left_node + right_node)//2
    update(index, value, left_node, mid, node*2)
    update(index, value, mid+1, right_node, node*2+1)

update(index=2, value=10)
print(tree)
# [0, 62, 22, 40, 13, 9, 21, 19, 3, 10, 4, 5, 13, 8, 9, 10, 1, 2, 0, 0, 0, 0, 0, 0, 6, 7, 0, 0, ...]

전체코드

arr = [1,2,3,4,5,6,7,8,9,10,]
tree = [0] * (len(arr)*4)

# 함수 호출 횟수 체크
call_def = 0

def init(left_node=0, right_node=len(arr)-1, node=1):
    if left_node == right_node:
        tree[node] = arr[left_node]
        return tree[node]
    mid = (left_node+right_node)//2
    tree[node] = init(left_node, mid, node*2) + init(mid+1, right_node, node*2+1)
    return tree[node]

def segment_sum(start, end, left_node=0, right_node=len(arr)-1, node=1):
    global call_def
    # 범위 밖에 있는 경우
    call_def += 1
    if start > right_node or end < left_node:
        return 0
    # 범위 안에 있는 경우
    if start <= left_node and right_node <= end:
        print(f"구간 {left_node}~{right_node} : {tree[node]}")
        return tree[node]
    mid = (left_node+right_node)//2
    return segment_sum(start, end, left_node, mid, node*2) + segment_sum(start, end, mid+1, right_node, node*2+1)

def update(index, value, left_node=0, right_node=len(arr)-1, node=1):
    if index < left_node or index > right_node:
        return
    # 범위 안에 있으면
    tree[node] += value-arr[index]
    if left_node == right_node:
        return
    mid = (left_node + right_node)//2
    update(index, value, left_node, mid, node*2)
    update(index, value, mid+1, right_node, node*2+1)

init() # segment tree init
print(tree)

res = segment_sum(2, 9) # 
print(f"합은 {res}, 함수는 {call_def}번 호출되었습니다.")

update(index=2, value=10)
print(tree)

이미지는 피그마를 활용하여 제작하였습니다.