참고자료
- [한빛미디어] 이것이 취업을 위한 코딩 테스트다 with 파이썬 (나동빈 저)
- https://github.com/ndb796/python-for-coding-test
0. 최단 경로 문제
최단 경로 알고리즘은 가장 짧은 경로를 찾는 알고리즘을 의미한다.
- 다양한 문제 상황
- 한 지점에서 다른 한 지점까지의 최단 경로
- 한 지점에서 다른 모든 지점까지의 최단 경로
- 모든 지점에서 다른 모든 지점까지의 최단 경로
- 각 지점은 그래프에서 노드로 표현
- 지점 간 연결된 도로는 그래프에서 간선으로 표현
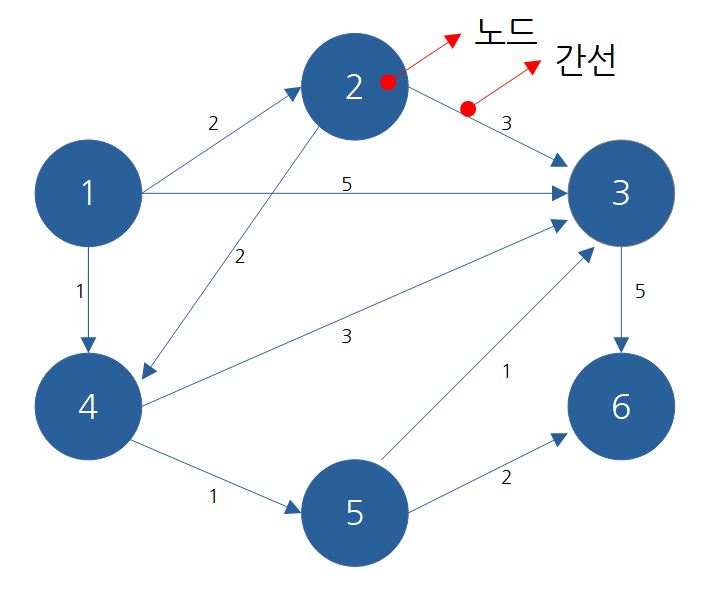
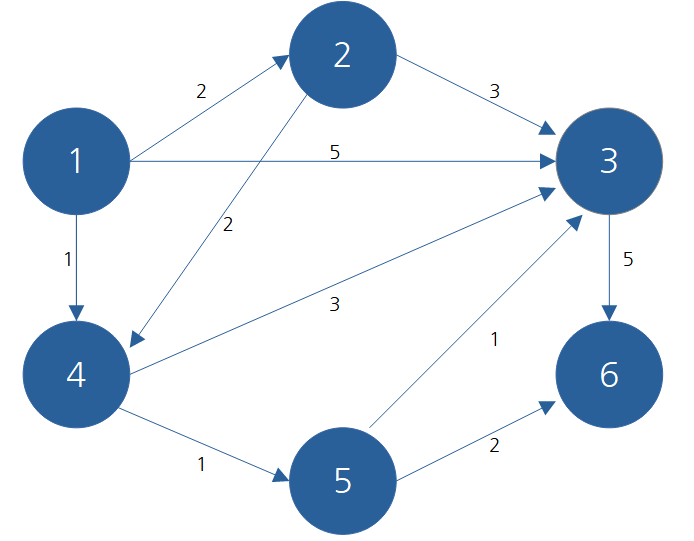
1번 노드에서 2번 노드로 이동이 가능하다고 하면 위와 같이 하나의 간선 형태로 표현이 가능하다. 이와 같이 특정 노드에서 다른 특정 노드로 이동이 가능하다고 하면 방향성이 있는 간선으로 표현한다.
1. 다익스트라 알고리즘이란?
다익스트라 알고리즘은 음의 가중치(음의 간선, 음의 값)가 없는 그래프의 한 노드에서 각 모든 노드까지의 최단거리를 구하는 알고리즘을 말한다.
'에츠허르 비버 다익스트라'가 고안한 대표적인 최단 경로 알고리즘이며 다익스트라가 제안한 알고리즘 중에서 가장 대표적인 알고리즘이 다익스트라 최단 경로 알고리즘이기 때문에 흔히 이를 줄여서 다익스트라 알고리즘이라고 부르기도 한다.
가능한 적은 비용으로 가장 빠르게 해답에 도달하는 경로를 찾아내는 알고리즘이기 때문에 네비게이션과 같은 문제에 응용된다.
- 특정한 노드에서 출발하여 다른 모든 노드로 가는 최단 경로를 계산
- 다익스트라 최단 경로 알고리즘은 음의 간선이 없을 때 정상적으로 동작
- 현실 세계의 도로는 음의 간선으로 표현되지 않음
- 다익스트라 최단 경로 알고리즘은 그리디 알고리즘으로 분류
- 매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정을 반복
2. 동작 과정
1) 출발 노드 설정
2) 최단 거리 테이블 초기화
3) 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택
(그리디 알고리즘으로 볼 수 있음)
4) 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신
5) 3~4과정 반복
단계0
출발 노드 설정 및 최단 거리 테이블 초기화
출발 : 1번노드
노드 번호 1 2 3 4 5 6 거리 0 무한 무한 무한 무한 무한
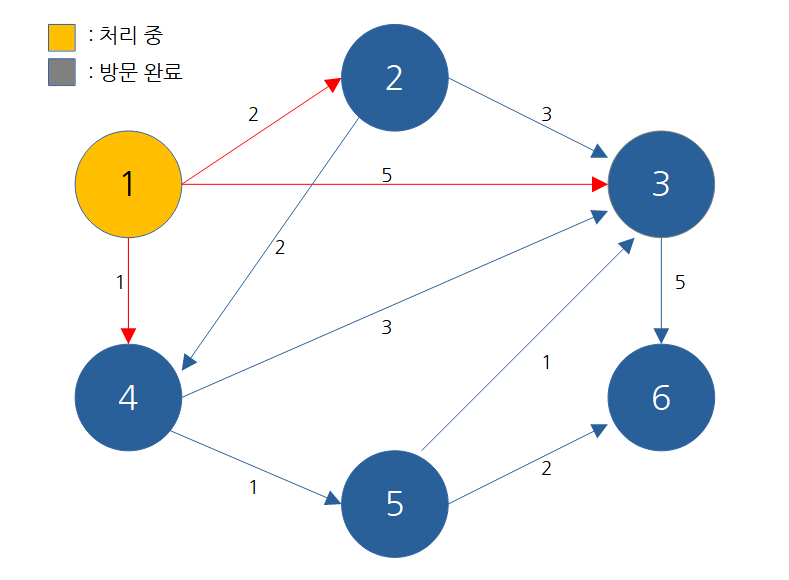
단계1
방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택 -> 1번
노드 번호 1 2 3 4 5 6 거리 0 2 5 1 무한 무한
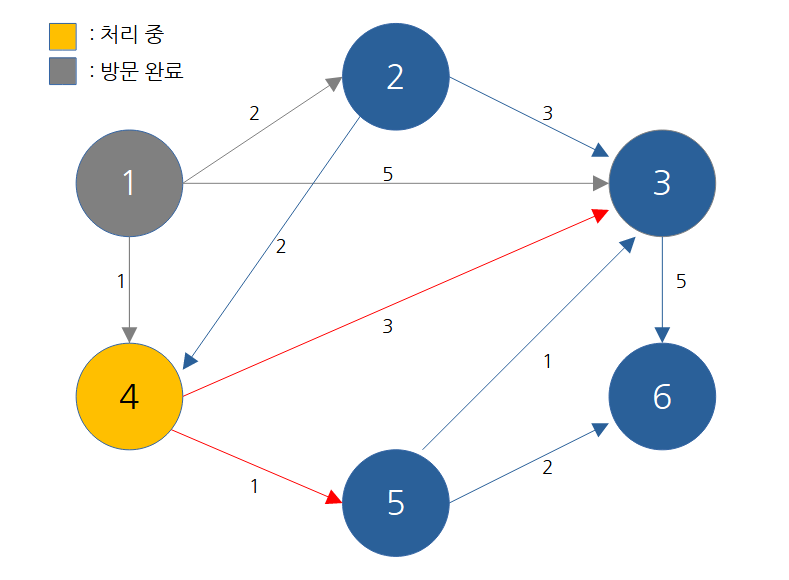
단계2
방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택 -> 4번
인접 노드 현재 값 거쳐갈 때 3번 5 1+3 5번 무한 1+1
해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신
노드 번호 1 2 3 4 5 6 거리 0 2 4 1 무한 무한
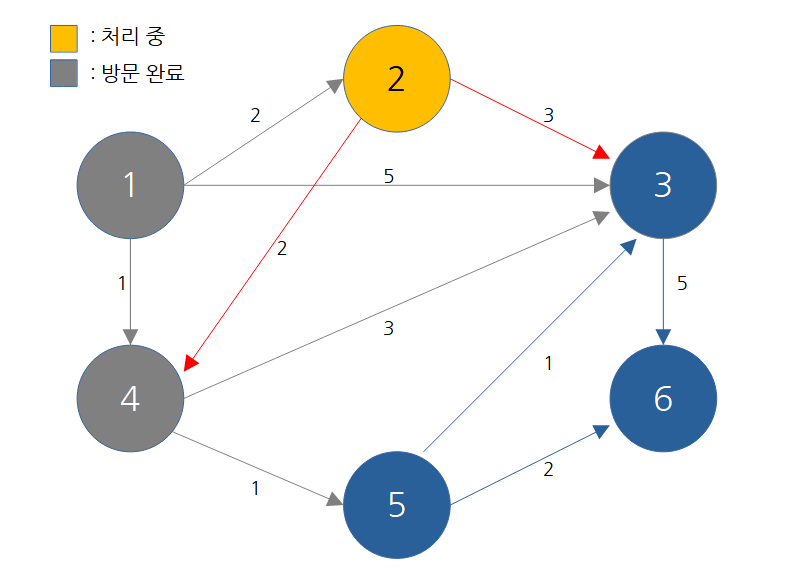
단계3
방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택 -> 2번
인접 노드 현재 값 거쳐갈 때 3번 4 2+3 4번 1 2+2
해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신
노드 번호 1 2 3 4 5 6 거리 0 2 4 1 2 무한
단계4
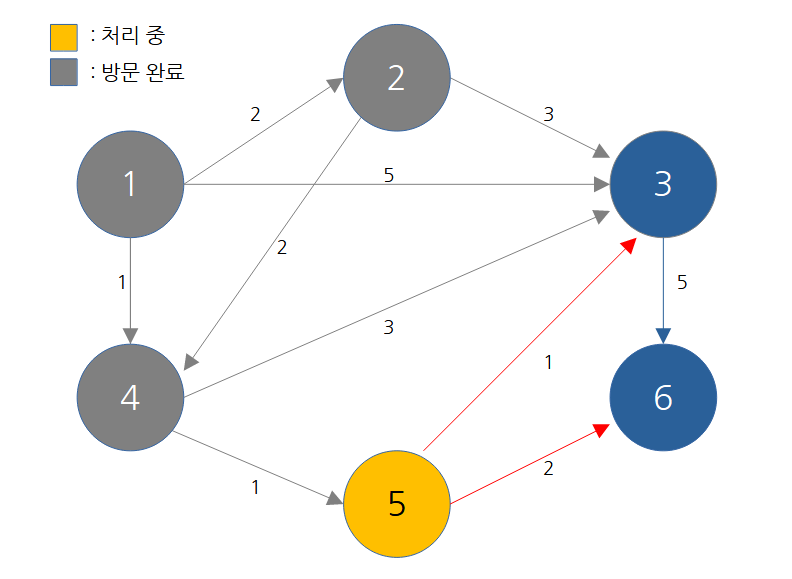
방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택 -> 5번
인접 노드 현재 값 거쳐갈 때 3번 4 2+1 6번 무한 2+2
해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신
노드 번호 1 2 3 4 5 6 거리 0 2 3 1 2 4
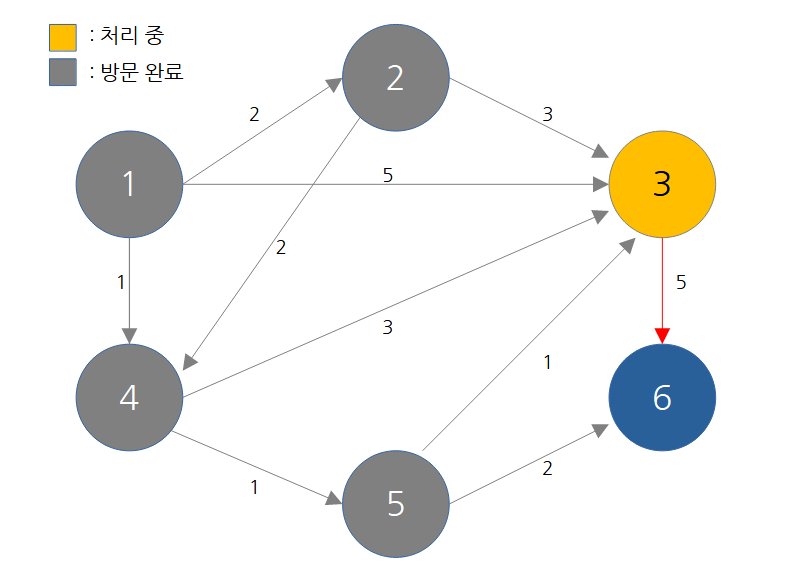
단계5
방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택 -> 3번
인접 노드 현재 값 거쳐갈 때 6번 4 3+5
해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신
노드 번호 1 2 3 4 5 6 거리 0 2 3 1 2 4
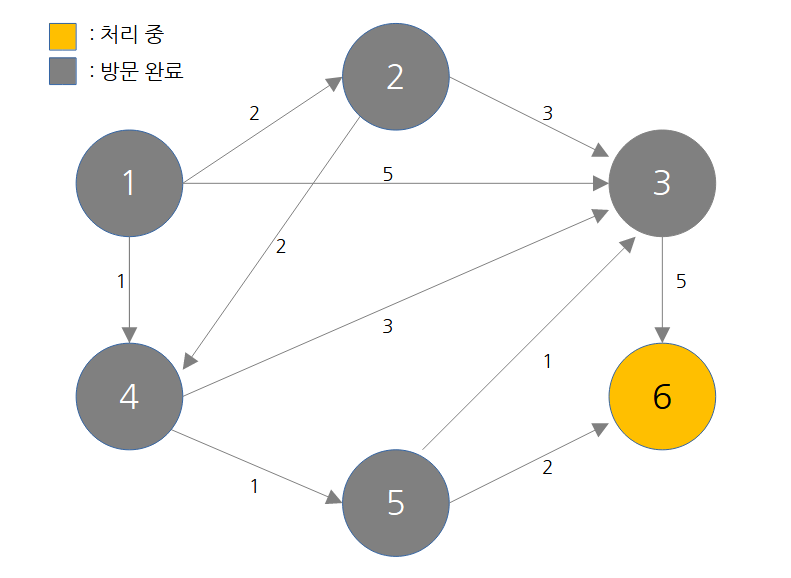
단계6
방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택 -> 6번
인접 노드 현재 값 거쳐갈 때 이동불가 - -
해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신
노드 번호 1 2 3 4 5 6 거리 0 2 3 1 2 4
3. 성능
다익스트라 알고리즘은 총 O(V)번에 걸쳐 최단 거리가 가장 짧은 노드를 매번 선형탐색해야 한다.
때문에 전체 시간 복잡도는 O(V^2)이다.
일반적으로 코딩 테스트의 최단 경로 문제에서 전체 노드의 개수가 적다면 다익스트라 알고리즘으로 충분히 문제를 해결할 수 있지만 노드의 개수가 10,000개를 넘어가는 문제라면 1억건 이상의 연산을 수행하므로 오래걸릴것이다.