삽입 정렬(Insert Sort)

개념

한 장을 뽑아 앞 자료들과 비교하며 제자리를 찾아간다.

• key 값은 두 번째 자료부터

구체적인 개념

• 삽입 정렬은 두 번째 자료부터 시작하여 그 앞(왼쪽)의 자료들과 비교하여 삽입할 위치를 지정한 후 자료를 뒤로 옮기고 지정한 자리에 자료를 삽입하여 정렬하는 알고리즘이다.
• 즉, 두 번째 자료는 첫 번째 자료, 세 번째 자료는 두 번째와 첫 번째 자료, 네 번째 자료는 - 세 번째, 두 번째, 첫 번째 자료와 비교한 후 자료가 삽입될 위치를 찾는다. 자료가 삽입될 위치를 찾았다면 그 위치에 자료를 삽입하기 위해 자료를 한 칸씩 뒤로 이동시킨다.
  
  
  

예시

배열에 8, 5, 6, 2, 4가 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해 보자.

코드

def insertionSort(arr):
    n = len(arr)
    for i in range(1,n):
        key = i # i를 뽑는다 
        for j in range(i-1,-1,-1): #j는 i전꺼 부터 거꾸로
            if arr[key] <= arr[j]: # 뽑은게 j보다 작으면
                arr[key], arr[j] = arr[j], arr[key] # 둘이 바꿔주고
                key = j # k에다 j를 넣어줘야 arr[key]가 뽑은 카드로 유지된다
        
arr = [8, 5, 6, 2, 4,1,3,7,9]
insertionSort(arr)
print(arr)

특징

• 장점
  - 안정한 정렬 방법
  - 레코드의 수가 적을 경우 알고리즘 자체가 매우 간단하므로 다른 복잡한 정렬 방법보다 유 리할 수 있다.
  - 대부분위 레코드가 이미 정렬되어 있는 경우에 매우 효율적일 수 있다.
• 단점
  - 비교적 많은 레코드들의 이동을 포함한다.
  - 레코드 수가 많고 레코드 크기가 클 경우에 적합하지 않다.

시간복잡도

최선의 경우

비교 횟수

• 이동 없이 1번의 비교만 이루어진다.
• 외부 루프: (n-1)번
• Best T(n) = O(n)

최악의 경우(입력 자료가 역순일 경우)

비교 횟수

• 외부 루프 안의 각 반복마다 i번의 비교 수행
• 외부 루프: (n-1) + (n-2) + … + 2 + 1 = n(n-1)/2 = O(n^2)

교환 횟수

• 외부 루프의 각 단계마다 (i+2)번의 이동 발생
• n(n-1)/2 + 2(n-1) = (n^2+3n-4)/2 = O(n^2)
• Worst T(n) = O(n^2)

[출처]https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html

---

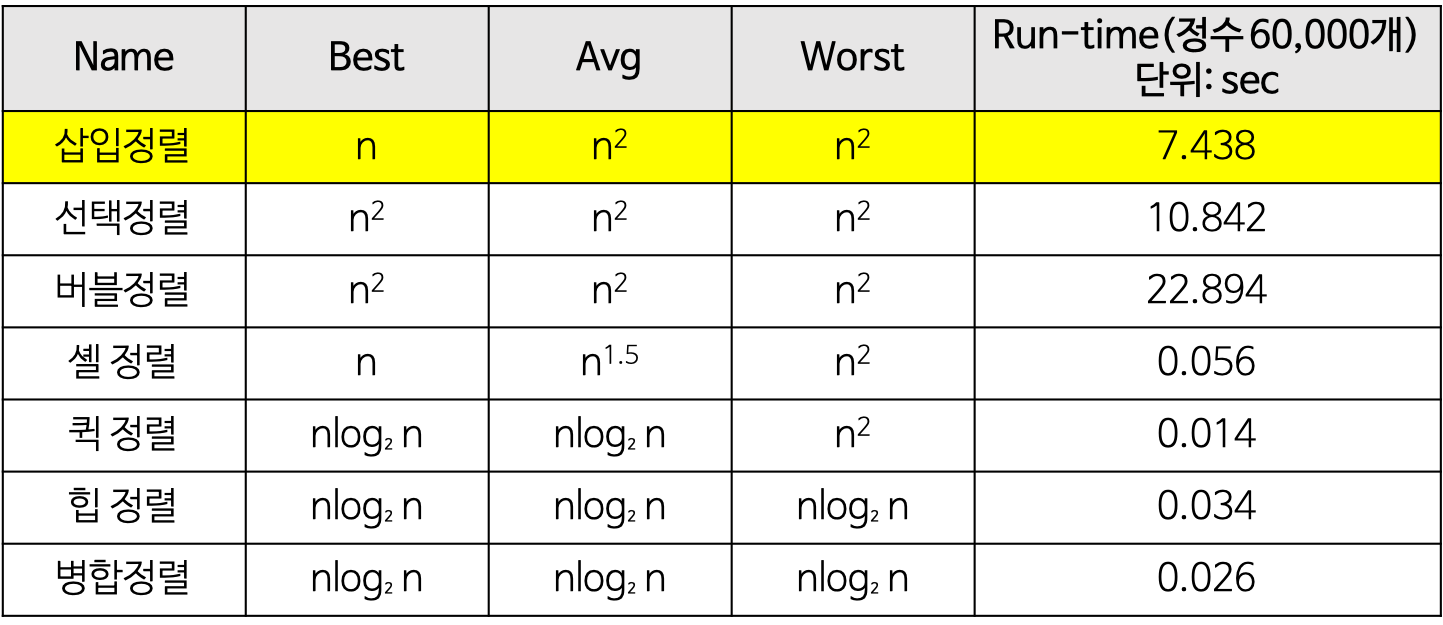
정렬 알고리즘 시간복잡도 비교