https://programmers.co.kr/learn/courses/30/lessons/49189

문제 설명

n개의 노드가 있는 그래프가 있습니다. 각 노드는 1부터 n까지 번호가 적혀있습니다. 1번 노드에서 가장 멀리 떨어진 노드의 갯수를 구하려고 합니다. 가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다.

노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 vertex가 매개변수로 주어질 때, 1번 노드로부터 가장 멀리 떨어진 노드가 몇 개인지를 return 하도록 solution 함수를 작성해주세요.

제한사항

• 노드의 개수 n은 2 이상 20,000 이하입니다.
• 간선은 양방향이며 총 1개 이상 50,000개 이하의 간선이 있습니다.
• vertex 배열 각 행 [a, b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.

풀이

이번 문제는 전형적인 BFS문제라 쉽게 풀 수 있었다.
다만,
인접 행렬과 인접 리스트의 차이점을 잘 몰라서 시간초과가 났다.

먼저 처음에 인접 행렬로 푼 코드이다.

def solution(n, edge):
    answer = 0
    g = [[0 for _ in range(n+1)]for _ in range(n+1)]
    visited = [0]*(n+1)
    for e in edge:
        g[e[0]][e[1]] = 1
        g[e[1]][e[0]] = 1

    q = deque()
    layer = 1
    q.append((1, layer))
    visited[1] = 1
    history = []
    while q:
        now, n_layer = q.popleft()
        history.append((now, n_layer))
        for i in range(len(g[now])):
            if g[now][i] == 1 and visited[i] == 0:
                visited[i] = 1
                q.append((i, n_layer+1))

    history.sort(key=lambda x: x[1], reverse=True)
    maxEdge = history[0][1]
    for h in history:
        if h[1] == maxEdge:
            answer += 1
        else:
            break
    return answer

0 0 0 0 0 0 0
0 0 1 1 0 0 0
0 1 0 1 1 1 0
0 1 1 0 1 0 1
0 0 1 1 0 0 0
0 0 1 0 0 0 0
0 0 0 1 0 0 0

이런식으로 행렬을 만들어 풀었다.
근데 만약에 n이 2만이라면?
공간 복잡도도 어마어마해지고 시간 복잡도도 어마어마하다

인접 리스트로 푼 코드를 살펴 보겠다.

def solution(n, edge):
    answer = 0
    visited = [0]*(n+1)
    arr = [[]for _ in range(n+1)]  # 인접리스트
    for e in edge:
        arr[e[0]].append(e[1])
        arr[e[1]].append(e[0])
    q = deque()
    layer = 1
    q.append((1, layer))
    visited[1] = 1
    history = []
    while q:
        now, n_layer = q.popleft()
        history.append((now, n_layer))
        for i in arr[now]:
            if visited[i] == 0:
                visited[i] = 1
                q.append((i, n_layer+1))

    history.sort(key=lambda x: x[1], reverse=True)
    maxEdge = history[0][1]
    for h in history:
        if h[1] == maxEdge:
            answer += 1
        else:
            break
    return answer

arr이라는 인접 리스트를 만들고
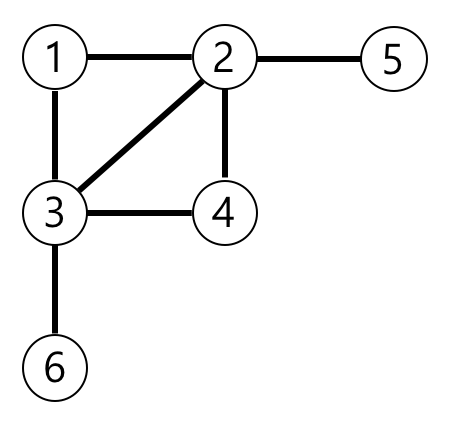
arr[1] : [2,3]
arr[2] : [1,3,4,5]
arr[3] : [1,2,4,6]
arr[4] : [2,3]
arr[5] : [2]
arr[6] : [3]
각각의 자리에 인접하는 노드를 넣어줬다(순서와 상관없음).
모든 노드들을 방문해야하는데 edge의 개수의 비례하게 탐색하면된다.

정리

인접 행렬

장점

• 구현이 쉽다

• 노드 i와 노드 j가 연결되어 있는지 확인하고 싶을 때, indexing으로 접근하기 때문에 O(1)의 시간 복잡도를 가진다

단점

• 전체 노드의 개수를 V개, 간선의 개수를 E개라고 하면, 노드 i에 연결된 모든 노드들에 방문하고 싶은 경우 adj[i][1]부터 adj[i][V]를 모두 확인해봐야 하기 때문에 총 O(V)의 시간이 걸린다.

• 노드의 수에 비해 간선의 개수가 훨씬 적은 그래프면 적절하지 않다.

인접 리스트

장점

• 실제 연결된 노드에 대한 정보만 저장하기 때문에, 모든 원소의 개수의 합이 간선의 개수와 동일하다

• 즉, 간선의 개수에 비례하는 메모리만 차지하여 구현이 가능하다

• 각 노드에 연결된 모든 노드들을 방문해 보아야 하는 경우, 인접 리스트로 연결 관계를 저장하는 것이 시간상 큰 이점을 가진다

단점

• 노드 i와 노드 j의 연결 여부를 알고 싶을 때, adj[i] 리스트를 순회하며 j 원소가 존재하는지 확인해야 한다 - 시간복잡도 O(V)

• 인접 행렬은 adj[i][j]가 1인지 0인지만 확인하면 i와 v 노드의 연결 여부를 O(1)로 확인 가능하다

노드의 연결여부를 알고 싶다면 인접 행렬
모든 노드를 돌아야한다면 인접 리스트