벡터가 뭔가요?
- 목차
- 벡터란
- 벡터 연산
- 벡터의 노름
- 두 벡터사이의 거리, 각도
- 내적
벡터란
- 벡터는 숫자를 원소로 가지는 리스트(list) 또는 배열(array)이다.
- 벡터는 공간에서 한 점을 나타낸다.
- 벡터는 원점으로부터 상대적 위치를 표현한다.
벡터 연산
- 스칼라 곱
- 백터에 스칼라곱을 하여 벡터의 길이를 변화시킬 수 있다.
- 성분곱(Hadamard product)
- 벡터끼리 같은 모양을 가지면 성분곱을 계산할 수 있다.
- 같은 모양을 가지면 덧셈, 뺄셈이 가능함
- 덧셈 : 다른 벡터로부터 상대적 위치이동을 표현한다.
- 뺄셈 : 방향을 뒤집은 덧셈
벡터의 노름
- 벡터의 노름(norm)은 원점에서부터의 거리를 말한다.
- -노름
- 각 성분의 변화량의 절대값을 모두 더한 것
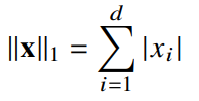
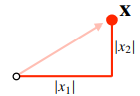
- 각 성분의 변화량의 절대값을 모두 더한 것
- -노름
- 피타고라스 정리를 이용해 유클리드 거리를 계산한 것
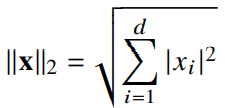
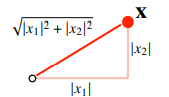
- 피타고라스 정리를 이용해 유클리드 거리를 계산한 것
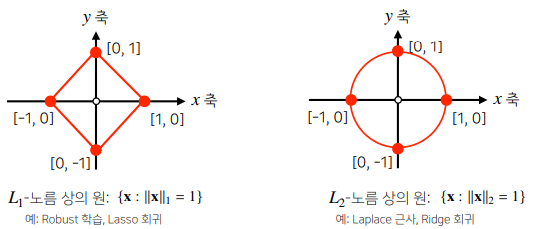
- -노름
- 노름은 그 종류에 따라 기하학적 성질(원에 대한 관점)이 달라짐
두 벡터 사이의 거리
- 노름을 이용해 두 벡터 사이의 거리를 계산할 수 있음
-
두 벡터사이의 거리를 계산할 때는 벡터의 뺄셈을 이용함
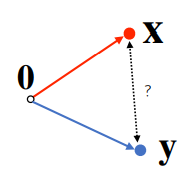
위 그림에서 X->Y의 길이는 ?
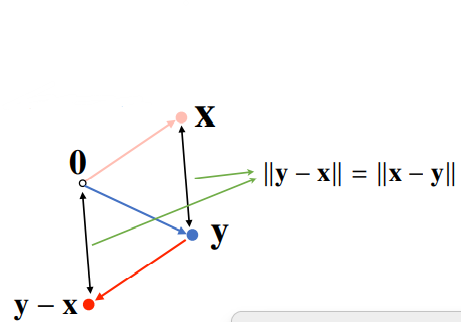
원점에서 y-x 까지의 거리와 같다 !
-
두 벡터 사이의 각도
- (노름만 가능) 두 벡터 사이의 거리를 알면, 제2 코사인 법칙을 통해 두 벡터 사이의 각도를 계산할 수 있다.
제2 코사인 법칙 참고
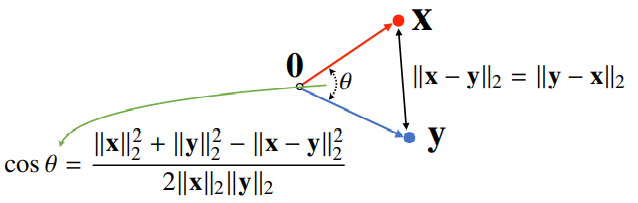
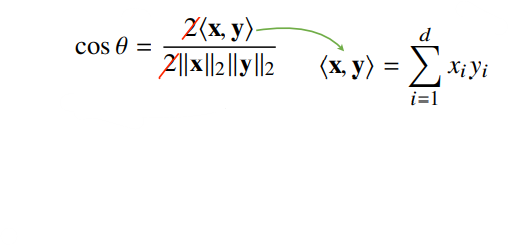
이러한 연산을 내적(inner product)이라 부른다.
내적 : 벡터들을 성분곱한 뒤, 이를 모두 더해주는 것
내적
-
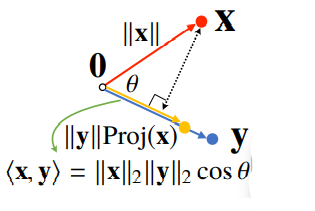
내적은 정사영(orthogonal projection)된 벡터의 길이와 관련 있다.
** 내적은 두 벡터의 유사도를 측정하기 위해 많이 사용된다.
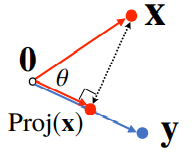
proj(x)는 벡터y로 정사영된 벡터 x의 그림자를 의미함
-
proj(x)의 길이는 코사인법칙에 의해 cos 가 된다.
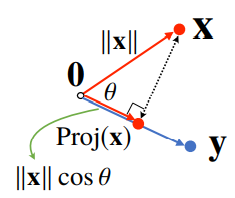
-
결국, 내적은 정사영의 길이를 벡터 y의 길이 ||y||만큼 조정한 값이다.