백준 1432 | 그래프 수정 (위상정렬, 우선순위 큐)

문제 출처 : https://www.acmicpc.net/problem/1432

문제

• n 개의 정점이 있는 그래프가 주어진다.
• 모든 정점의 번호는 1보다 크거나 같고 n보다 작거나 같다.
• 조건 :
  • v1에서 v2로 연결된 간선이 있다면, v2의 번호는 v1보다 커야 한다.
• 위 조건을 이용하여 그래프의 번호를 다시 매긴 후에, 1번 정점의 새로 고친 번호를 m1, 2번 정점의 새로 고친 번호를 m2, ... , n번 정점의 새로 고친 번호를 mn 이라고 하면, n개의 수열이 만들어진다.
• 이 수열을 출력하는 프로그램을 작성하시오

입력

• 첫째 줄에 정점의 개수 n 주어진다. ( 1 <= n <= 50 )
• 둘째 줄부터 n개의 줄에는 인접행렬 형식으로 입력이 주어진다.
  • 0 : 연결되지 않았음
  • 1 : 연결 되었음

출력

• 첫째 줄에 수열의 각 원소를 차례대로 공백을 사이에 두고 출력한다.
• 그래프의 번호를 수정할 수 없다면 -1 출력
• 답이 여러 개일 경우 사전 순으로 제일 앞서는 것을 출력

위상 정렬의 동작 방법

1. 노드 및 간선 개수를 입력
2. 모든 노드의 진입/진출 차수를 0으로 초기화
3. 각 노드에 연결된 간선정보를 담기 위한 연결 리스트를 초기화
4. 방향 그래프의 모든 간선 정보를 입력받고, 이때 입력받으면서 진입차수 테이블을 갱신
   (Topology Sort 함수)
5. 알고리즘 수행 결과를 저장할 리스트 생성
6. 처음 시작시 진입 차수가 0인 노드 큐에 삽입
7. 큐가 빌 때까지 아래 내용 반복
   1) 큐에서 원소 꺼내기 (꺼내면서 결과 리스트에 추가)
   2) 해당 노드와 연결된 노드들의 진입 차수 빼기
   3) 7-2)의 과정에서 새롭게 진입 차수가 0이 되는 노드 큐에 삽입
8. 결과 출력 (끝 ~ !)

문제 접근 방법

• 위상 정렬과 우선순위 큐를 이용하여 풀었다.
• 이 문제는 크게 3개의 조건을 잘 이용해서 풀어야 한다.

1. 문제의 조건에서 v1에서 v2로 가는 간선이 있다면 v2가 v1보다 커야한다.
2. 답이 여러 개 일 경우 사전순으로 출력해라.
3. 만약 그래프의 번호를 수정할 수 없다면 -1 을 출력해라.

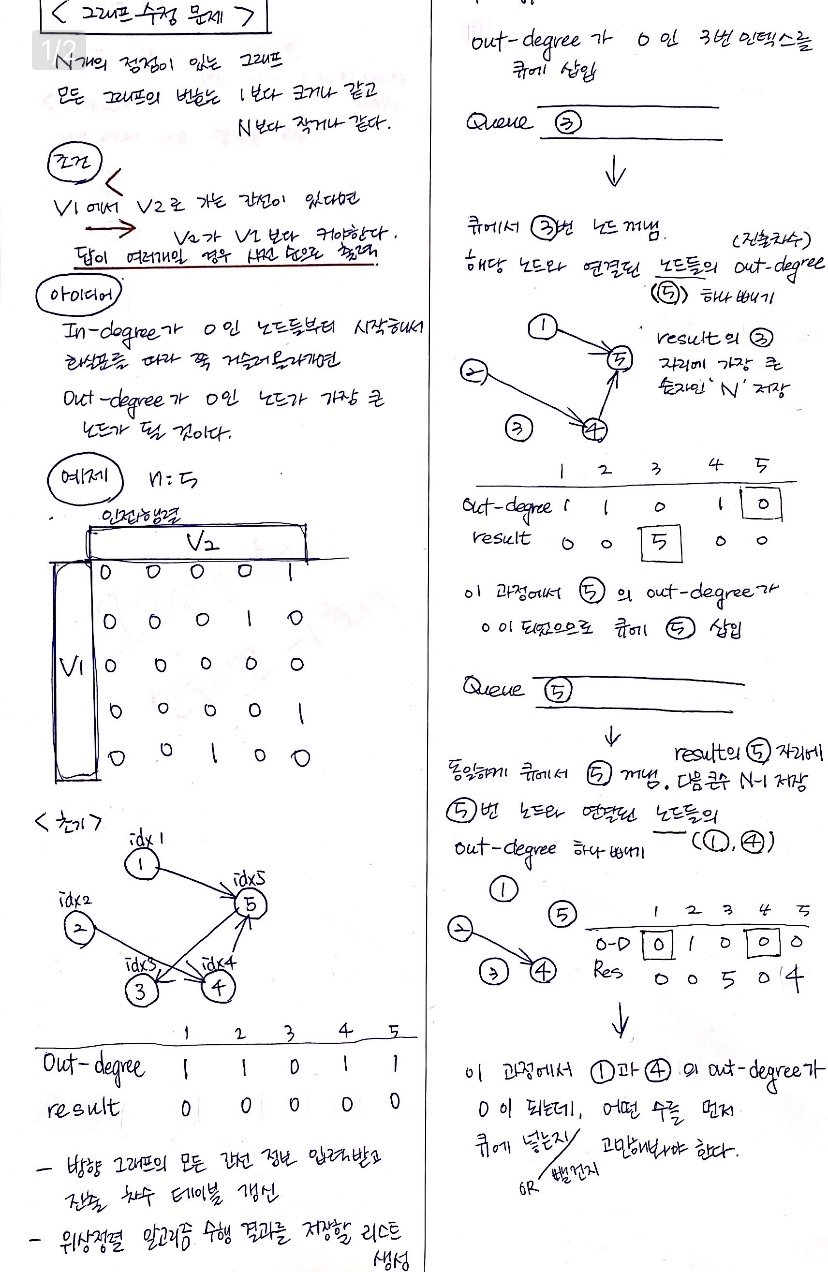
과정 1

문제의 조건에서 v1에서 v2로 가는 간선이 있다면 v2가 v1보다 커야한다.

• 진입 차수(In-degree)가 0 인 노드들부터 시작해서 화살표를 따라 쭉 거슬러 올라가면
  진출 차수(Out-degree)가 0인 노드를 만나게 되고 그 노드가 가장 큰 노드가 될 것이다.
• 따라서 위상 정렬을 이용하여
  1. 초기에 진출 차수(Out-degree)가 0인 정점에 가장 큰 수를 넣고
  2. 해당 정점과 연결된 정점들의 진출 차수를 1 빼면서
  3. 그 과정에서 진출 차수가 0인 정점을 큐에 넣는 과정의 반복을 통해
  4. 큰 수부터 차례로 작은 수를 result 리스트에 저장한다.

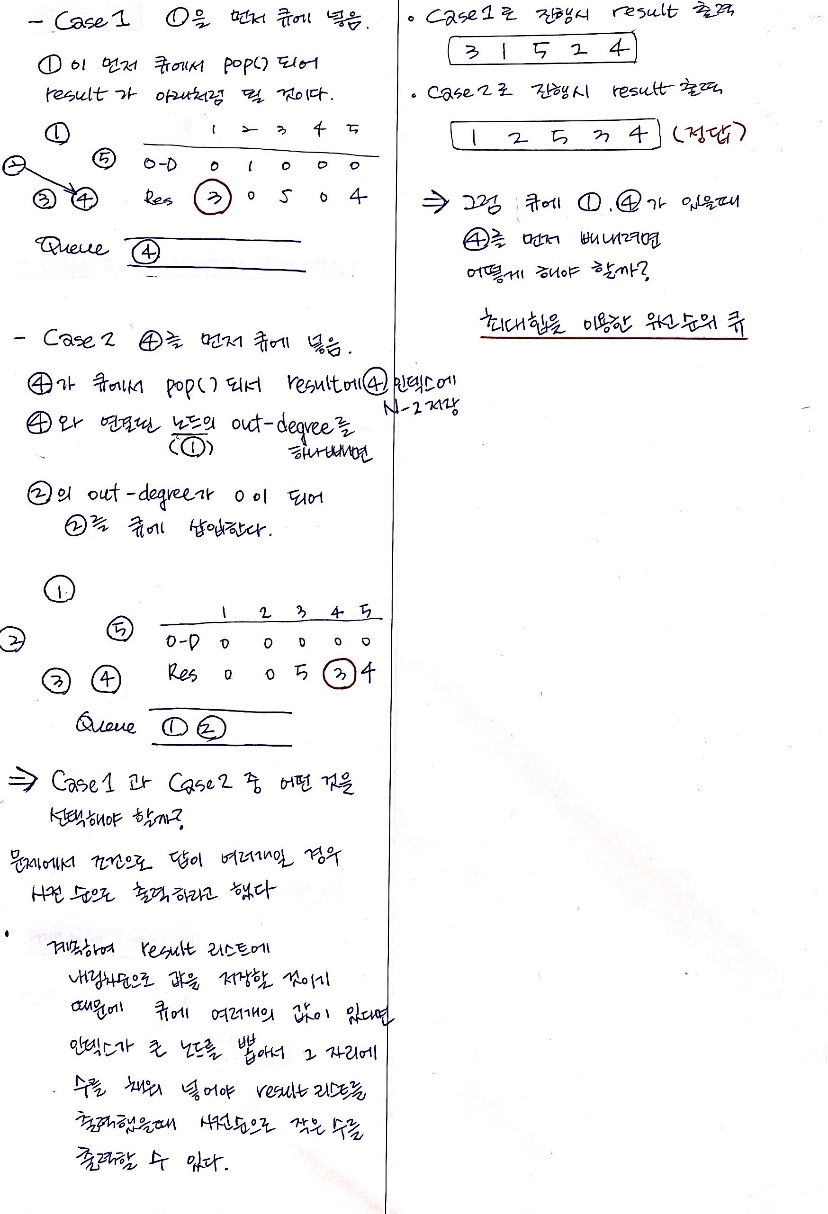
과정 2

답이 여러 개 일 경우 사전순으로 출력해라.

result_1 = [ 3, 1, 5, 2, 4 ]
result_2 = [ 1, 2, 5, 3, 4 ]

위 와 같은 경우에는 31524 > 12534 이므로 result_2 가 사전 순으로 작은 수 이다.
더 작은 인덱스(0번)에 더 작은 수가 있을 수록 사전순으로 작은 수가 출력된다.

• 문제 접근 방법 1을 통해 위상 정렬을 통해 큐에 진출 차수가 0인 정점들이 저장된다.
• 큐에서 먼저 꺼내는 정점에는 상대적으로 더 큰 수(번호)를 저장한다.
  • 따라서 큐에 진출차수가 0인 정점이 여러개 있을 때,
    사전 순으로 출력하기 위해서는 인덱스가 큰(뒤)에 있는 인덱스를 큐에서 먼저 꺼내야
    나중에 0번 인덱스부터 n번 인덱스까지 차례로 출력했을 때
    더 작은 수가 출력된다.

과정 3

• 만약 그래프의 번호를 수정할 수 없다면, 사이클이 생겨서 위상정렬을 수행할 수 없다는 의미이다.
• 사이클이 생기려면 최소 3개 이상의 정점이 필요하다.
• 위상 정렬을 통해 사이클을 형성하는 정점에 들어와서 그 정점과 연결된 진입/진출 차수를 뺀다고 해도 나머지 정점들이 큐에 들어가지 않게 되어 위상 정렬이 제대로 수행되지 않는다.
• 위상정렬이 제대로 수행되지 않는다면 결과(result)에 값이 변하지 않는다.

코드

import heapq

n = int(input())

# 각 노드에 연결된 간선 정보를 담기 위한 연결 리스트 초기화
graph = [[] for _ in range(n + 1)]

# 모든 노드에 대한 진출차수는 0으로 초기화
outdegree = [0] * (n + 1)

# 결과 정보 저장을 위한 result 변수 선언 및 초기화
result = [0] * (n + 1)

# 방향 그래프의 모든 간선 정보를 입력 받기
for i in range(1, n + 1):
    connection = list(map(int, input()))
    
    # 인접행렬에서 인접한 노드들만 graph 리스트에 추가
    for idx, val in enumerate(connection):
        if val == 1:
            graph[idx + 1].append(i)
            outdegree[i] += 1

# 위상 정렬
def topology_sort(n):
    # 큐에 여러 노드가 있을 경우 인덱스가 큰 노드를 먼저 큐에서 빼기 위해 우선순위 큐(heapq) 사용
    # ( 답이 여러 개일 경우 사전 순으로 제일 앞서는 것 출력하기 위해서 )
    heap = []

    # 차수 0인 노드 큐에 삽입
    for i in range(1, n + 1):
        if outdegree[i] == 0:
            heapq.heappush(heap, -i)

    while heap:
        # 우선순위 큐를 이용하여 큐에서 인덱스가 가장 큰 노드 꺼내고
        # 해당 노드와 연결된 노드들의 진출 차수 빼기
        # 큐에서 빼낸 노드번호를 인덱스로 result 리스트에 가장 큰 숫자 (n) 저장 
        # 이 과정에서 새롭게 진출 차수가 0이 되는 노드 큐에 삽입
        now = -heapq.heappop(heap)
        result[now] = n

        for connected_node in graph[now]:
            outdegree[connected_node] -= 1
            if outdegree[connected_node] == 0:
                heapq.heappush(heap, -connected_node)

        n -= 1

topology_sort(n)

# 사이클이 돌아서 그래프 번호를 수정할 수 없다는는 노드가 2개 이상이라면 -1 출력
# 사이클이 돌려면 최소 3개의 노드가 서로를 가리키고 있어야하는데 
# 그러면 2개이상의 노드는 진출 차수가 0이 될 수 없어서 큐에 넣을 수 없다.
if result.count(0) > 2:
    print(-1)
else:
    # print(*result[1:])
    print(' '.join(map(str, result[1:])))

정리 노트

더 알아볼 것

• 같은 방식으로 진입 차수(In-degree)를 이용한 위상정렬과 최소힙을 이용한 우선순위 큐를 이용하여 코드를 작성하면 안되는 이유 알아보기
  • 참고 ) https://syogeng.wordpress.com/2017/09/06/test/