문제 : https://www.acmicpc.net/problem/5639
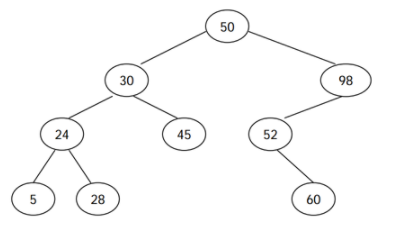
문제 해결 아이디어
- 이진 검색 트리의 경우
- 왼쪽 서브 트리의 노드들은 루트의 값보다 키가 작고,
- 오른쪽 서브 트리의 노드들은 루트의 값보다 키가 크다
문제에서 입력은 전위 순회*로 노드들을 방문한 결과이다.
-
전위 순회는 루트노드 - 왼쪽 서브트리 - 오른쪽 서브트리 순으로 방문한다.
- 따라서 배열의 0번 인덱스는 루트 노드의 값임을 알 수 있다.
-
또한 이진 검색트리의 조건에 따라
- 왼쪽 서브트리의 노드들은 모두 루트 노드보다 크기가 작고,
- 오른쪽 서브 트리의 노드들은 모두 루트 노드보다 크기가 크기때문에
- 입력된 리스트에서 루트노드보다 첫번째 큰 노드 이후의 리스트는 루트 노드의 오른쪽 서브트리임으로 알 수 있다.
-
루트노드 : 첫번재 인덱스
-
오른쪽 서브트리 : 루트보다 큰 값의 인덱스 ~ 끝까지
-
왼쪽 서브트리 : 루트 + 1 인덱스 ~ 루트보다 큰 값의 인덱스 - 1
임을 알 수 있으므로, 각 서브트리에 대해서도 재귀적으로 루트노드, 왼쪽 서브 트리, 오른쪽 서브트리를 찾는다.
⚡ 주의 ⚡
만약 루트노드보다 큰 값이 없을 경우에는
루트 노드를 제외한 나머지 노드들이 왼쪽 서브트리에 있다는 의미이므로
for loop을 돌면서 right_idx의 값을 + 1 씩 증가시켜주어야 한다.
import sys
sys.setrecursionlimit(10 ** 6)
preorder_list = []
while True:
try:
preorder_list.append(int(sys.stdin.readline()))
except:
break
def postorder(start, end):
# 종료 조건
if start > end:
return
# 변수 초기화
# root : 해당 트리의 루트 노드 값
# right_idx 해당 트리의 오른족 서브 트리 인덱스
root = preorder_list[start]
right_idx = start + 1
# 루트보다 큰 값의 인덱스 찾기 (오른쪽 서브트리)
for i in range(start + 1, end + 1):
right_idx = i
if preorder_list[i] > root:
break
# print(f'root : {root}, right_idx : {right_idx}, right_val : {preorder_list[right_idx]}')
# 왼쪽, 오른쪽 서브트리에 대해서 재귀적으로 다시 트리를 타고 들어감
# 후위순회 (왼쪽, 오른쪽, 루트)
postorder(start + 1, right_idx - 1)
postorder(right_idx, end)
print(root)
postorder(0, len(preorder_list) - 1)