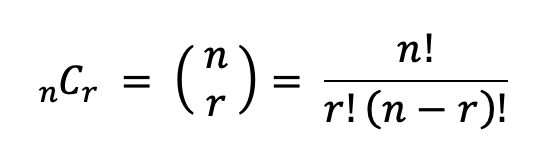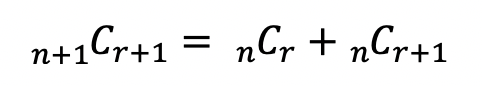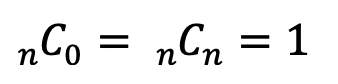동적 계획법이란?
DP, 즉 동적 계획법은 하나의 큰 문제를 여러 개의 작은 문제로 쪼개어서 그 결과를 저장하여 다시 큰 문제를 접근하여 해결할때 사용 된다.
일반적으로 재귀(recursive) 방식 또한 DP와 유사하다. 차이점으로는 재귀는 일반적은 재귀를 단순하게 사용하기에 불필요한 작업이 반복되어 비효율적인 시간이 낭비된다.
예를 들어 피보나치 수를 구하고 싶을때 대게 재귀함수를 이용한다.
return f(n) = f(n-1) + f(n-2)여기서 두 f(n-1), f(n-2) 함수에서 각각 호출되어 동일한 값을 2번 계산하게 되고 ㅇ호출 되는 함수의 횟수는 기하급수적으로 늘어나게 된다.

위의 그림에서 DP를 활용하게 되면 시간복잡도를 다음과 같이 줄일 수 있다.
O(n^2) -> O(f(n)), f(n) = 다항식 수준
DP의 사용 조건
1. Overlapping Subproblems
DP는 기본적으로 문제를 나누고 그 문제의 결과 값을 재활용하여 최종 답을 구한다. 때문에 동일한 작은 문제들이 반복되는 경우에 사용이 가능하다.
위에 그림에서 양쪽의 자식 노드에서 f(2) 부분이 4번이나 반복되는데 이것을 계산 1회를 통해서 나머지 3회의 값을 재활용을 통해 이용할 수 있는 것이다.
2. Optimal Substructure
부분 문제의 최적 결과 값을 이용하여 전체 문제의 최적 결과를 낼 수 있는 경우이다.
부분 문제의 결과값이 전체 문제에 대입 하였을때에도 결과가 변하지 않을때 DP를 사용할 수 있는 것이다.
DP 사용 방법
DP는 특정한 알고리즘이 아니라 하나의 방법론이기에 다양한 문제해결에 쓰인다. 때문에 문제를 보고 DP가 적용 가능한 것인지 파악이 중요하다.
DP는 과정은 아래와 같다.
1) DP로 해결 가능한 문제인지 판단
2) 문제의 변수를 파악
3) 변수 간 점화식(관계식)을 생성
4) memoization(top down) or tabulation(bottom up)
5) 기저 상태 확인
6) 구현
DP 구현 방법
1. Bottom up
이름에서 보이듯이, 아래에서 부터 계산을 누적하여 전체 큰 문제를 해결하는 방식이다.
메모를 위해 dp라는 배열은 생성후 dp[0]가 기저 상태이고 dp[n]을 구하고자 하는 값이라고 하자.
즉 dp[0]부터 시작하여 반복문을 통해 dp[n]까지 값을 전이시켜 재활용 하는 것이다.
2. Top down
이 방식은 dp[0]의 기저 상태에서 시작하여 dp[n]의 값을 찾기 위해 위에서 부터 바로 호출을 시작하여 dp[0]의 상태까지 내려가 해당 결과값을 재귀를 통해 전이 시켜 재활용하는 방식이다.
피보나치 예시처럼 f(n)= f(n-1) + f(n-2)의 과정에서 n=5일때 f(3), f(2)의 동일한 계산이 포함되고 가장 최근의 상태 값을 메모해 두었다고 해서 memoization이라고 부르는 것이다.
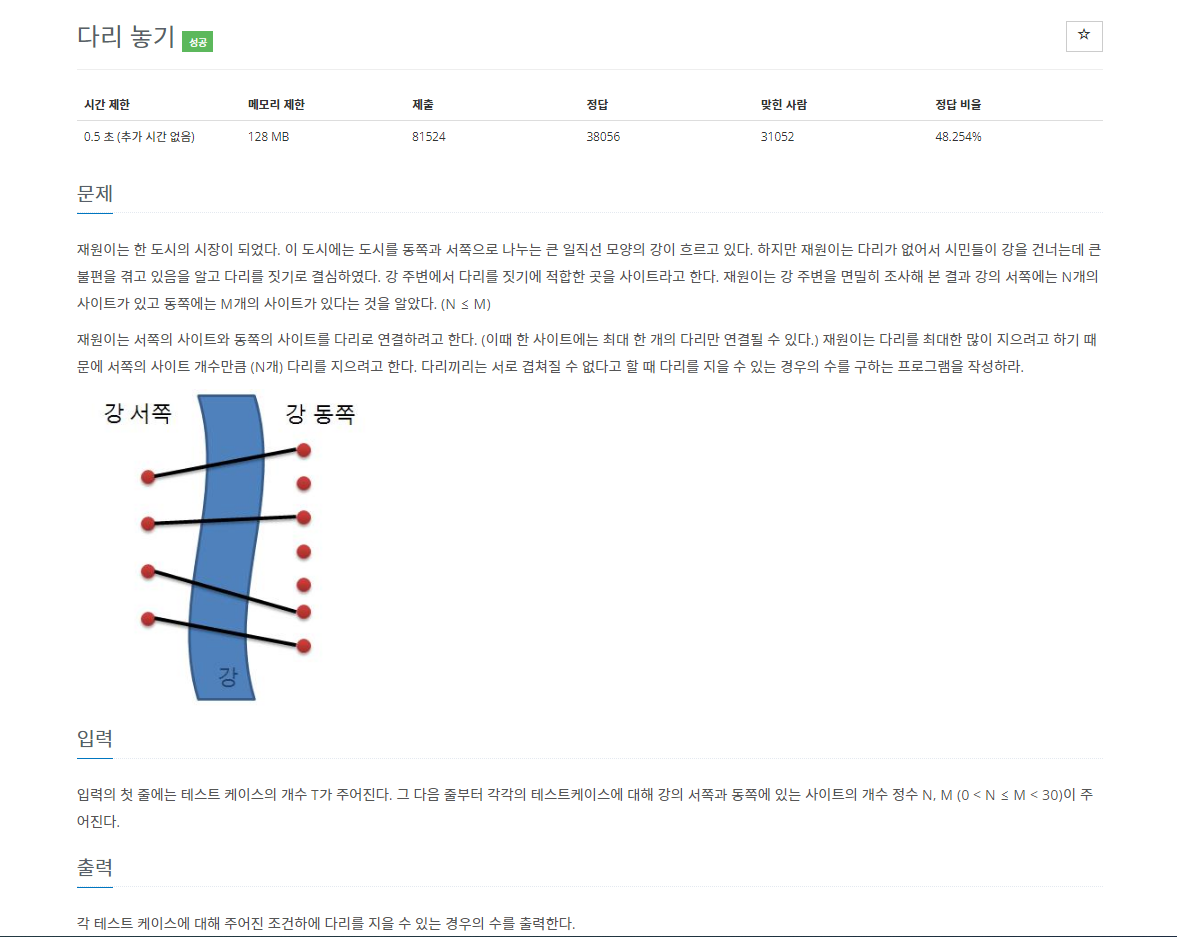
다음 문제를 통해 이해를 높여보자
이 문제는 시간 제한이 촉박한 문제이다. 문제를 보면 겹치면 안되고 N <= M인 조건에서 M개에서 N개를 선택 중복이 되면 안된다. 여기서 Combination 공식을 찾는다면 처음 접근은 쉽다.
-조합의 1번 성질
-조합의 2번 성질
2가지의 성질을 memoization을 이용하면 코드는 쉽게 구현가능하며 문제의 변수 dp배열에서 값이 주어졌다면 계산과정을 넘어가는 코드를 추가하여 시간 제한을 해결할 수 있다.
import java.util.Scanner;
public class Main {
static int[][]dp = new int[30][30];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
StringBuilder sb = new StringBuilder();
for(int i=0; i<T;i++){
int N = sc.nextInt();
int M = sc.nextInt();
sb.append(combi(M,N)).append("\n");
}
System.out.println(sb);
}
public static int combi(int n, int r){
if(dp[n][r] > 0)
return dp[n][r];
if(n == r || r == 0)
return dp[n][r] = 1;
dp[n][r] = combi(n-1, r-1) + combi(n-1, r);
return combi(n-1, r-1) + combi(n-1, r);
}
}
정리
이번시간에 DP에 대해서 알려진 것에 비해 아주 간단하게 다루어 보았다. 다음에 기회가 되면 더 자세하게 알아보았다.