[알고리즘] 탐욕 알고리즘(Greedy Algorithm)

그리디 알고리즘 (Greedy Algorithm)이란?

1. 매 순간 최적 또는 최선의 경우를 선택하는 방식으로 최적의 값을 도출하는 방식이다.
2. 그 시점의 선택이 가장 좋아 보이지만 목적지에 도달했을때 최적의 해가 아닐 수 있다.
3. 즉 매 순간 가장 좋은 결과를 도출하지만 결과적으로는 최적의 해를 보장해 주지 않는다.

그리디 알고리즘의 정당성

그리디 알고리즘을 적용 가능한 문제는 두가지의 조건을 만족해야한다.
1.greedy choice property: 현재의 선택이 이 후의 선택에 영향을 주지 않는다.
2.optimal substructure: 매 순간의 최적의 해가 문제 전체에 대해 최적의 해여야 한다.

그리디 알고리즘의 장점

알고리즘의 설명이 쉬우며 최적의 해를 구한다는 가정에서 계산 속도가 타 알고리즘에 비해 빠르다.(하지만 모든 경우에 그렇지는 않다.)

그리디 알고리즘의 단점

순간의 선택이 항상 최적이라는 보장이 없기에 문제에 접근할 때는 보장된다는 가정을 참으로 두고 문제에 접근해야 한다.

예를 들어 루트에서 리프까지 아래 그래프에서 가중치가 큰 경로를 찾고자 한다.

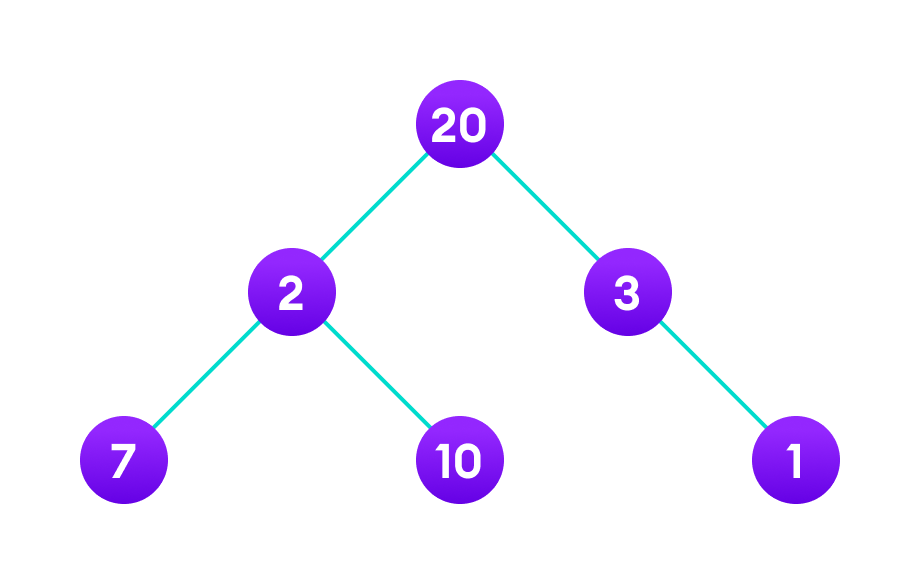
접근 방식

1.루트노드에서 시작하며 오른쪽의 가중치는 3 왼쪽의 가중치는 2이다.
2.현재 최적의 해는 3임으로 오른쪽을 석택한다.
3.마지막으로 3의 마지막 리프 노드는 1이며 결과값은 20 + 3 + 1 = 24이다.

하지만 2의 오른쪽 자식노드의 가중치는 10 결과값은 20 + 2 + 10 = 32이다.
결국에 그리디 알고리즘은 항상 최적의 솔류션을 제공하지 않는 것이다.

그리디 알고리즘 적용

가장 일반적은 예로 동전을 이용한 거스름돈 문제가 있다.
[백준] 11047 문제: 동전0

---

가장 큰 단위의 동전부터 생각하여 거스름돈을 줄여 나간다면 쉽게 해결할 수 있는 문제이다.

1. 동전의 종류에 대해 오름차순을 이용해서 입력받은 동전의 종류를 배열에 넣는다.
2. 반복문을 이용해서 입련된 K에서 큰 단위부터 나누어 떨어지는 만큼 빼준다.
3. K의 값이 나누어 떨어질 때마다 cnt의 값을 갱신해주며 K또한 갱신한다.
4. K의 값이 0이 되면 동전 개수의 최솟값(cnt)를 출력한다.

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        int K = sc.nextInt();
        int[] coin = new int[K];

        for(int i=0 ;i<N; i++)
           	coin[i] = sc.nextInt();

        int cnt =0;
        for(int i =N-1; i >= 0; i--){
            if(K == 0)
                break;
            if(coin[i] <= K){
                cnt += K / coin[i];
                K = K % coin[i];
            }
        }
        System.out.println(cnt);
    }
}

이 문제에서 그리디 알고리즘의 특징은 가장 큰단위의 동전부터 선택하여 계산하는 부분이다.

정리

다음 시간에는 브루트포스 알고리즘에 대해 다루어 본다.