[Algorithm] 순열과 조합

1. 순열

1. 개념

• n개의 수에서 r개를 순서 있게 뽑는 경우의 수

2. 접근 방법

• 재귀를 이용한다.
  

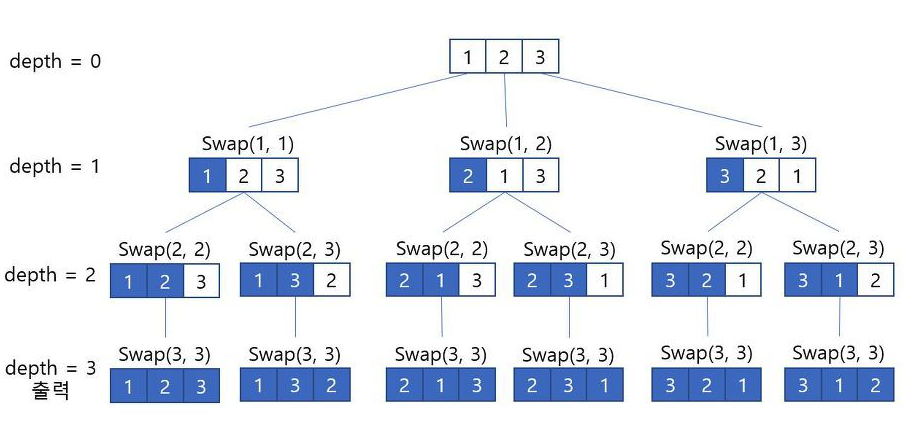
3. 구현 코드

	static int permutationCount = 0;
    
    public void permutation(int[] arr, int n, int r, int depth){
        if(depth == r) {
            System.out.println(Arrays.toString(Arrays.copyOfRange(arr, 0, 3)));
            permutationCount++;
        }
        for(int i = depth; i < n; i++){
            swap(arr, i, depth);
            permutation(arr, n, r, depth + 1);
            swap(arr, i, depth);
        }
    }

    public void swap(int[] arr, int i, int depth) {
        int tmp = arr[i];
        arr[i] = arr[depth];
        arr[depth] = tmp;
    }

2. 조합

1. 개념

• n개의 수에서 r개를 순서 상관없이 뽑는 경우의 수

2. 접근 방법

• 재귀를 이용한다.

• 중첩 for문 사용한다.
  - 선택하는 수가 3개 이상일 때는 재귀로 해결한다.

  • 3개까지는 for문을 이용하자 -> 메모리 효율 + 속도가 더 빠름

3. 구현 코드

• 재귀 방식

    int n = 5;
    int k = 3;
    int[] a = {1,2,3,4,5};
    public void printList(ArrayList<Integer> arr)
    {
        for(int i = 0; i < arr.size(); i++){
            System.out.print(a[arr.get(i)]);
        }
        System.out.println();
    }

    public void combi(int start, ArrayList<Integer> arr){
        if(arr.size() == k) {
            printList(arr);
            return;
        }
        for(int i = start + 1; i < n; i++){
            arr.add(i);
            combi(i, arr);
            arr.remove(arr.size() - 1);
        }
    }
    
    public void solution() {
        ArrayList<Integer> arr = new ArrayList<>();
        combi(-1 , arr);
    }