Squeeze-and-Excitation Networks(SENet)을 읽고 내용을 정리하고자 한다.

주의 : 내용이 중구난방,,입니다

개요

convolutional neural network는 spatial, channel-wise한 정보를 서로 융합시키는 방법으로 informative feature를 추출하고 이를 통해 representation을 생성해낸다. 이러한 강력한 CNN의 성능이 계층적 pattern을 학습하여 image에 대해 강력한 descriptor가 될 수 있음이 증명되어왔다. 더 나아가 성능을 더욱 향상시키기 위해서 당시 많은 연구들은 representation을 boost하기 위한 'spatial encoding'에 집중되어 있었다. (ex. inception 등)

저자들은 많은 연구들이 관심을 가진 spatial encoding 보다는 channel relationship에 집중을 하고, 새로운 architecture인 SENet을 발표한다.

아래에서 기술하겠지만 SENet을 간략하게 언급하고 넘어가자면, channel간의 interdependency을 반영하여 channel-wise feature를 중요도에 따라 recalibration(재조정)하는 과정인 Squeeze-and-Excitation(SE) block으로 이루어진 network이다.

SENet은 기존의 architecture에도 쉽게 적용될 수 있다는 점과 SE block을 network에 추가함으로써 생기는 파라미터의 증가 수 대비 성능의 향상도가 더 높다는 점이 특징으로 뽑힌다.

SENet은 마지막 대회인 2017ILSVRC에서 top-5 error를 2.251%(2016 winning model 대비 약 25%감소)까지 줄이면서 1위를 달성했다.

Squeeze-and-Excitation Blocks

Figure 1은 SE block 연산과정을 도식화 한 것이다.

• SE block의 연산과정

1. $H^{'} \times W^{'} \times C^{'}$ 의 크기를 가진 $X$는 $F_{tr}$(convolution operation)연산을 통해 $H \times W \times C$ 크기를 가진 feature map $U$가 된다.
2. $U$는 $F_{sq}$(squeeze)을 거쳐서 $1 \times 1 \times C$가 된다. 이후 $F_{ex}$(excitation)를 거쳐서 channel 별로 가중치를 가진 channel descriptor를 얻는다.
3. 가중치가 입혀진 channel descriptor를 $U$와 channel-wise multiplication을 수행하여 SE block의 최종 output인 $\tilde{U}$(reweighted feature map)를 얻는다.

논문의 Figure1 에서는 최종 아웃풋을 $\tilde{X}$로 나타내고 있지만, $X$가 아닌 $U$에 scale을 적용해주는 것이기 때문에 $\tilde{U}$로 표현하는 것이 더 낫다고 생각하여 이하 $\tilde{X}$를 $\tilde{U}$로 표현하겠습니다.

what is $F_{tr}$ in Figure 1.

squeeze, excitation을 살펴보기 전에 가장 첫번째로 수행되는 연산인 $F_{tr}$에 대해서 정리한다.

$X=[x_1, x_2, ..., x_{C'}]$ - (input)
$U=[u_1, u_2, ..., u_{C}]$ - (output)
$V=[v_1, v_2, ..., v_{C}]$ - ($v_{C}$는 C번째 filter를 가르킨다.)
$v_c=[v_c^1, v_c^2, ..., v_c^{C'}]$

일 때, $F_{tr}$의 c-th filter의 output $u_c$는 아래와 같이 표현할 수 있다.

$u_c=v_c*X=\sum_{s=1}^{C'}v_c^s*x^s$

수식을 보면 알 수 있듯이 $F_{tr}$은 일반적인 convolution 연산과 같다.

$F_{tr}$을 설명한 저자들은 해당 section 말미에 아래와 같이 언급한다.

"Since the output is produced by a summation through all channels, the channel dependencies are implicitly embedded in vc, but these dependencies are entangled with the spatial correlation captured by the filters. Our goal is to ensure that the network is able to increase its sensitivity to informative features so that they can be exploited by subsequent transformations, and to suppress less useful ones. We propose to achieve this by explicitly modelling channel interdependencies to recalibrate filter responses in two steps, squeeze and excitation, before they are fed into next transformation."

위의 $F_{tr}$, 그러니까 convolution 연산의 output에 channel정보가 embedding되어 있지만, spatial correlation 또한 포함되어 있기 때문에 output이 충분하게 channel간 interdependency를 반영하지 못한다는 것이다.
따라서 이를 해결하고자 output에 추가적인 변형을 가하게 된다.
추가적인 변형은 앞서 언급한 SE block의 squeeze와 excitation이며, 이 두 가지 과정을 통해 filter를 재조정(recalibrate)하여 output이 channel interdependencies를 다시금 반영할 수 있도록 하는 것이다.

(개인적인 생각)
위 과정을 정리하다 보니까 든 생각이 있다.
Xception과 DenseNet과 같은 연구들이 convolution연산 대신 SEblock과 비슷한 맥락의 separable depthwise convolution을 사용한 것을 보면 SENet을 포함한 당시 연구들은 convolution의 연산이 spatial and channel dependency를 동시에 포착하는 것에 대한 비효율성에 대해 경계심을 가지고, 이를 해결하고자 하는 노력이 많았던 것 같다.

Squeeze: Global Information Embedding

저자들은 channel dependecy를 output에 어떻게 반영할지에 대한 문제를 다루기 위해서 먼저, output의 각 channel에 전해지는 신호를 고려했다.
하지만 학습된 각 filter는 local receptive field 영역 안에서 연산이 수행되기 때문에, output $U$는 local receptive field 밖의 상황정보(global spatial information)는 반영하기 어렵다는 문제가 있었다. Local receptive field가 매우 작은 네트워크의 초반 부분에서는 문제가 더욱 심각하게 작용한다.

이 문제를 완화하기 위해서 저자들은 global spatial information을 channel-descriptor로서 활용하는 squeeze를 제안한다.

squeeze는 아래 수식과 같이 $H \times X$를 $1 \times 1$ size로 줄이면서 단순하게 channel-wise statistics를 반영할 수 있는 global average pooling을 사용하여 문제를 해결한다.

$z_c=F_{sq}(u_c)=\frac{1}{H\times W}\sum_{i=1}^{H}\sum_{j=1}^{W}u_c(i, j)$

channel 별로 중요한 정보만을 압축하여 사용하는 것이라고 볼 수 있다.
squeeze의 output $z_c$는 이제 각 channel의 중요 정보를 반영하게 된 것이다!

Excitation: Adaptive Recalibration

이번 section에서는 squeeze 연산으로 집계된 channel 정보를 활용하기 위해서 channel-wise dependencies를 완전히 포착하는 것을 목표로 하는 두번째 연산 Excitation을 제안한다.

channel-wise dependencies를 완전히 포착하는 목표를 달성하기 위해서는 두가지 기준이 충족되어야 한다.

• 1. 유연한 구조
  다른 모델에 유연하게 적용하기 위해서 인듯하다.
  
  
• 2. non-mutually-exclusive relationship를 학습할 수 있어야 함.

저자들이 Excitation을 이용하는 것의 목표가 squeeze 연산으로 집계된 channel 정보를 활용하기 위해서임을 잊지말자.
이 목표를 달성하기 위해서는 각 channel마다 곱해질 가중치가 필요한데, mutually-exclusive relationship(one-hot activation)은 [1,0,0,0,0, ....]로 표현되어 scale을 표현할 수 없다.
non-mutually-exclusive relationship으로 Excitation연산을 구현하게 되면, [0.1, 0.4, 0.8, 0.3,.... ]와 같이 channel 별 weight를 구할 수 있기 때문에 궁극적으로는 저자들이 원하는 channel dependecy를 반영한 reweight를 진행할 수 있는 것이다.

non-mutually-exclusive relationship : [0.1, 0.4, 0.8, 0.3,.... ] <- sigmoid activation을 사용하여 0~1의 값을 가지도록 해서 channel에 곱해질 가중치가 될 수 있도록 설계함.
mutually-exclusive relationship(one-hot activation) : [1,0,0,0,0, ....] <- scale을 표현할 수 없음.

이 두가지 기준을 충족하기 위해 저자들은 sigmoid activation을 사용하는 간단한 gating mechanism을 채택했다.

$s=F_{ex}(z, W)= \sigma(g(z, W))=\sigma(W_2\delta(W_1z))$

$\delta$ - ReLU, $\sigma$ - sigmoid
$W_1$ dimensionality-reduction layer의 parameter
$W_2$ dimensionality-increasing layer의 parameter

• squeeze에서 GAP로 집계된 channel 정보를 그대로 activation map $U$에 곱해줄 수는 없다. 가중치를 조절해주기 위한 FC layer가 필요하다.
• SE block의 gating mechanism은 model complexity를 제한하면서 일반화된 모델을 위해, non-linearity 주위에 2개의 FC layer로 bottleneck을 형성하는 방식으로 구현된다.
• bottleneck은 reduction ratio $r$을 사용하여 간단하게 구현한다.

20개의 feature map, reduction ratio $r$ 4가 라면 위의 FCN 형상을 가진다.

단순 FC layer로 가중치를 재조절 하는 것에 더하여, bottleneck layer를 삽입해서 model의 복잡도를 낮추는 역할을 추가한 것이다.

마침내 SE block의 최종 output이 아래와 같이 구해진다.

$\tilde u_c = F_{scale}(u_c, s_c)=s_cu_c$

$F_{scale}$은 channel wise multiplication 연산이다.

0~1의 값을 가진 $s_c$가 $u_c$에 channel-wise로 곱해지면서, rescaling된(channel별 중요도를 반영한) $\tilde u_c$를 도출해낼 수 있다.

이후 section(The role of Excitation)에서 Excitation에 대한 실험을 진행한 결과 network 후위의 Excitation은 recalibration을 제대로 하지 못하는 것을 확인했다. 따라서 final stage의 SE block을 제거하면 parameter증가율을 4%로 줄이면서 0.1% 미만의 성능 손실만을 가져오기 때문에 파라미터 축소를 위해서는 마지막 레이어의 SE block은 제거하는게 더 낫다.

Exemplars: SE-Inception and SE-ResNet

resnet과 GoogleNet에 적용된 모습이다. SENet의 장점인 어떤 architecure에도 적용될 수 있는 유연성이 돋보이는 예이다.

Model and Conmputational Complexity

• SE block을 적용했을 때 추가되는 parameter의 갯수

  $\frac{2}{r}\sum_{s=1}^{S}N_s\cdot C_s^2$

  $S$는 스테이지의 수, $Cs$는 output channel의 차원, $Ns$는 스테이지 $S$에서 반복되는 블록의 갯수이다.

Implementation

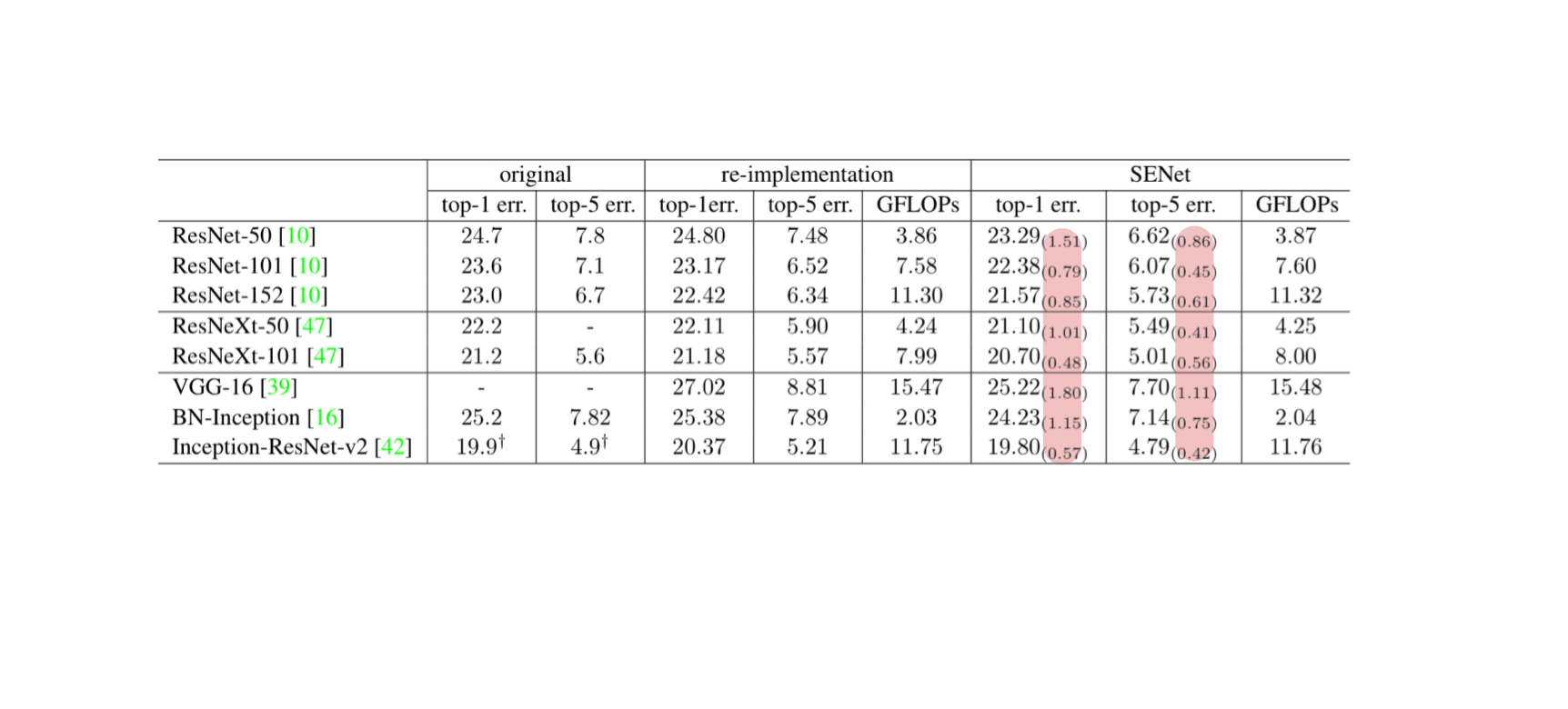
형광색으로 표시된 부분을 보면 SE block을 적용했을 때 error rate가 유의미하게 감소한 것을 확인할 수 있다.

Analysis and Interpretation

Reduction ratio

Reduction ratio $r$은 model 내의 SE block의 computational cost, capacity를 조절할 수 있는 중요한 hyper parameter이다.

연구진들은 $r$ 값을 조절하면서 생기는 결과를 보고 최적의 $r$ 찾고자했다.

위 그림은 SE-ResNet50에서 $r$ value를 조절하면서 실험한 결과이다.

$r$ value를 조절하면서 증가한 capacity가 model performance의 향상을 무조건적으로 보장하는 것이 아니라는 것을 확인할 수 있다.

따라서 연구진들은 위 결과를 참고하여, 모든 experiment에서의 $r$ value를 16으로 설정했다.

느낀점

SE block의 유연성에 대해서 확인하고, 해당 block을 다른 architecture에 적용할 수 있는 가능성에 대해서 알 수 있었다.

또한 지금까지 읽은 논문은 capactiy와 accuracy 간의 관계를 고려하지 않은 부분이 있었는데 SENet에서는 해당 관계의 trade off를 인지하고, 적절한 지점을 찾았다는 점이 재밌었다.