https://www.acmicpc.net/problem/12891
initial
I used .count(), which is O(n) method to calculate each a,c,g,t for each sliding window iteration. This is time inefficient.
I also converted the dna "cgatgaa" to "124421" numerical format but actually that doesnt change anything cuz count will work for both cases.
runtime error solution
n,k = map(int,input().split())
dna = str(input())
dna_lst = []
lst = list(map(int, input().split()))
a,c,g,t = lst[0],lst[1],lst[2],lst[3]
dic = {"A":1, "C":2, "G":3, "T":4}
count =0
for d in dna:
dna_lst.append(dic[d])
for i in range(len(dna_lst)-k+1):
window = dna_lst[i:i+k]
cntA, cntC, cntG, cntT = window.count(1), window.count(2), window.count(3), window.count(4)
if cntA>=a and cntC >= c and cntG >= g and cntT >= t:
count+=1
print(count)solution
remember sliding window is subtracting the leftmost element and adding the rightmost element.
There are 2 ways for sliding window, initialise sliding window is a must for both ways but whether you account that initialised sliding window before your main logic or within your main logic is your choice. The latter would be cleaner and to do so, you have to adjust your main logic which is a bit harder.
sliding window accounted before main logic
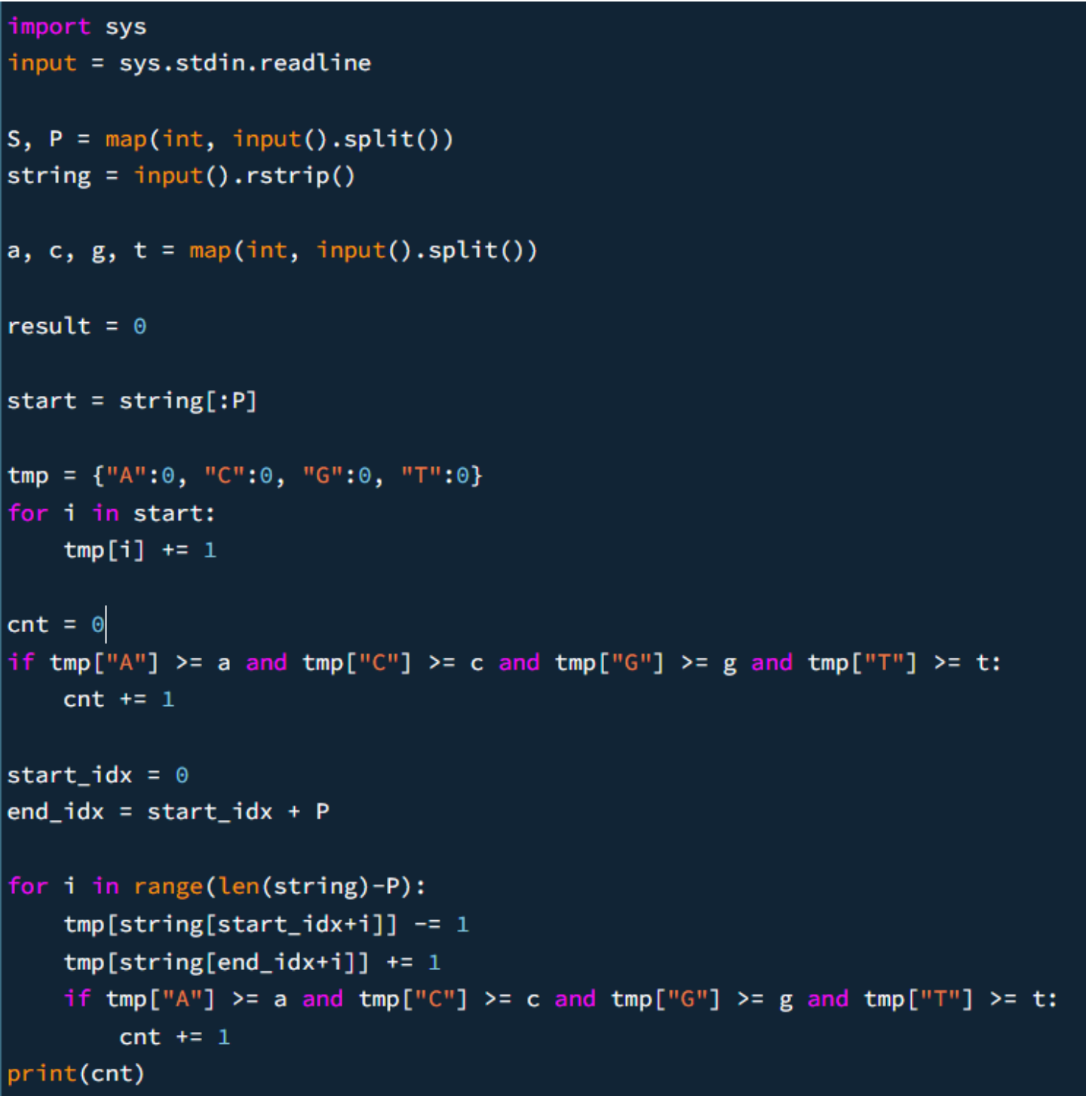
before the for loop main logic, we accounted for the initalised sliding window by incrementing count if we meet the condition.
sliding window accounted in main logic
This is cleaner but harder. How do we do this?
The way we initialise the sliding window is different.
window = dna[:k-1]. Notice the k-1. This is an incomplete sliding window, which will be filled up in the main for loop logic.
n,k = map(int,input().split())
dna = str(input())
a,c,g,t= map(int, input().split())
dic = {"A":0, "C":0, "G":0, "T":0}
# incomplete sliding window with the rightmost element not accounted for
# to fit in logic instead of calculating for initial window separately
window = dna[:k-1]
count =0
for i in window:
dic[i]+=1
left,right = 0,k-1
for i in range(len(dna)-k+1):
dic[dna[right]]+=1
if dic['A']>=a and dic['C']>=c and dic['G']>=g and dic['T']>=t:
count+=1
dic[dna[left]]-=1
left+=1
right+=1
print(count)So this main for loop logic works on incomplete sliding window that is missing the rightmost value at the start.
you can use while loop (while right < s) instead of for loop like
from collections import deque
s, p = map(int, input().split())
string = list(str(input()))
A, C, G, T = map(int, input().split())
dic = {'A': 0, 'C': 0, 'G': 0, 'T': 0}
left, right = 0, p-1
arr = deque(string[left:right])
for i in arr:
dic[i] += 1
cnt = 0
while right < s:
# 구간 완성
dic[string[right]] += 1 # 가장 오른쪽 원소 추가
# 계산
if dic['A'] >= A and dic['C'] >= C and dic['G'] >= G and dic['T'] >= T:
cnt += 1
# 구간이동
dic[string[left]] -= 1 # 가장 왼쪽 원소 제거
left += 1
right += 1
print(cnt)complexity
The code you provided seems to be an implementation of a sliding window approach to count the number of substrings of length k within a given DNA sequence (dna) that contain at least a 'A's, c 'C's, g 'G's, and t 'T's. Here's the complexity analysis of the code:
-
Initialization (Constant Time):
- Reading
nandkand creating thednastring take constant time.
- Reading
-
Initialization of
dic(Constant Time):- Creating the dictionary
dicwith four keys ('A', 'C', 'G', 'T') and initializing their values to 0 takes constant time since there are only four keys.
- Creating the dictionary
-
Sliding Window (Linear Time):
- The code uses a sliding window approach to scan through the DNA sequence. It maintains a window of size
kand slides it through the sequence. - The loop iterates
len(dna) - k + 1times, wherelen(dna)is the length of the DNA sequence. For each iteration, it updates thedicdictionary and checks if the conditionsdic['A'] >= a,dic['C'] >= c,dic['G'] >= g, anddic['T'] >= tare met. - Since each iteration of the loop involves constant time operations (updating the dictionary and checking conditions), and there are
len(dna) - k + 1iterations, the time complexity of the sliding window part is O(len(dna)).
- The code uses a sliding window approach to scan through the DNA sequence. It maintains a window of size
-
Printing (Constant Time):
- Printing the final count takes constant time.
Overall, the time complexity of the code is dominated by the sliding window part, which is O(len(dna)). The space complexity is also O(1) because the size of the dic dictionary remains constant regardless of the input size.
In summary, the code efficiently counts the number of substrings meeting specific conditions using a sliding window approach with a time complexity of O(len(dna)).