https://www.acmicpc.net/problem/2668
initial
I tried to solve via dictionary where I first stored all in a dictionary. Then, I tried seeing if there are matches like if we come across 3:1, I will look for 1:3 in my dictionary and if there is, increment count. Also if the key and value is same like 5:5, it is a valid case too so increment count.
my incorrect sol:
n=int(input())
dic={}
ans =[]
count=0
for i in range(1,n+1):
num = int(input())
dic[i]= num
for key in dic.keys():
val = dic[key]
if (val in dic and dic[val]==key) or key==val:
count+=1
ans.append(key)
print(count)
ans.sort()
for i in ans:
print(i)but think about this case
1 2 3 4
3 4 2 1
my dictionary solution will not work.
So after struggling, I googled and people solved via DFS.
solution
This question is trying to detect if there is a cycle. A cycle means that if we dfs and come back to an already visited node, that is a cycle. A cycle also represents that there are alternate pairs like 1-3 and 3-1 , or 5-5 that are present.
We first create an adjacency matrix like
# Graph
1: [2, 3]
2: []
3: [1]
4: [6]
5: [4, 5]
6: [7]
7: []Diagram wise, first example looks like
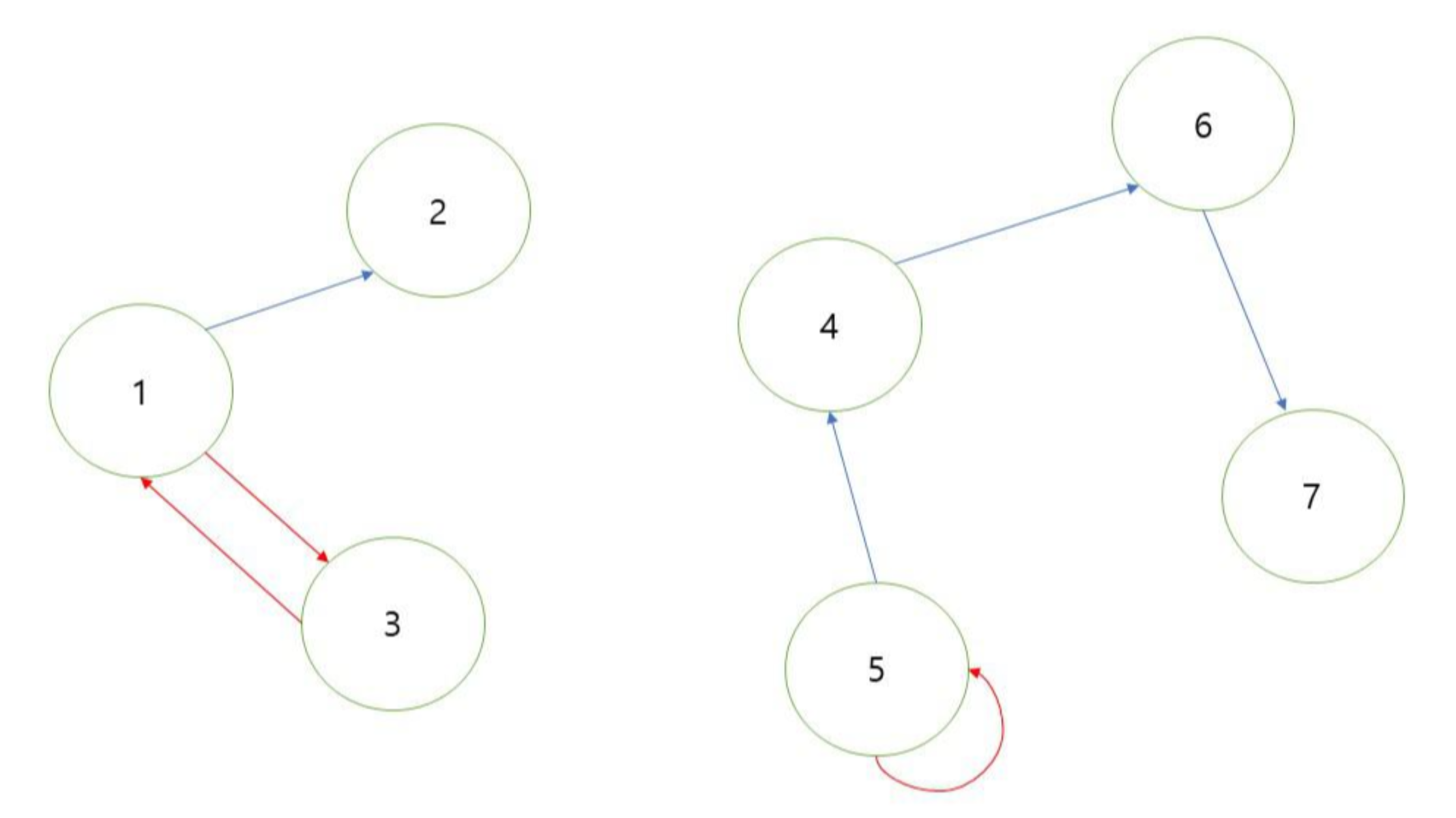
ref: https://cotak.tistory.com/141
I would have never thought of DFS, let alone detecting a cycle. need more practice of DFS other than just 2x2 board.
[need revision I still don't get it] my still wrong code:
n=int(input())
visited= [False for _ in range(n+1)]
graph = [[] for _ in range(n+1)]
for i in range(1,n+1):
num = int(input())
graph[num].append(i)
ans =[]
def dfs(node,check):
check.add(node)
visited[node]=True
for a in graph[node]:
if not visited[a]:
dfs(a, check.copy())
else:
ans.extend(list(check))
return
for i in range(1,num+1):
if not visited[i]:
dfs(i,set([]))
ans.sort()
print(len(ans))
for i in ans:
print(i)[revisited 13th jan] so creating the adj matrix like that is the most important step, where the 2nd row nodes point to the first row nodes, making it unidirectional. I just blindly made the connection and I got something like
1:3, 2:1, 3:1, 4:5, etc which is the same way as initial that I did months ago. So no improvement till now lol.
So make the adj matrix like that. Only then we can see the pattern.
I missed the key point of this question. We have to add all nodes in the joint set. What I mean is we cant do ans.append(node) like we used to but our answer list must append all the nodes in that 1 dfs search. So we have to use extend() to append all elements from an iterable. So for example 1 dfs search we have [1,7], it means we have to add 1 AND 7 to answer list via extend(), not just 1 element.