[백준] 3109번: 빵집

https://www.acmicpc.net/problem/3109

initial

THe question is wrong it shouldnt be row. It should be from column 1 to column [-1].

Greedy in a way that we want our path to be in as up and ascending as possible. Because if our paths are in downwards direction, it might interfere other future paths which may need to go up to reach the last column. So we priorities diagonal up move as the first direction, just to the right at same row as second direction and no choice but diagonally right down as third direction. We then do dfs on it and when we reach the last column, we increment count.

The way i took the string graph input was wrong. I did just like an integer graph like [list(map(int,input().split()] but since the input is already a string, it doesnt map to the graph properly. We should do it like graph=[list(input().strip()) for _ in range(n)]

but why is this giving more available paths for this code (hint: once we meet the right condition, we continue on with the rest of the directions. we have to finish the entire dfs loop)

n, m = map(int, input().split())
graph=[list(input().strip()) for _ in range(n)]
count = 0
dy = [1, 1, 1]
dx = [-1, 0, 1]
visited = [[False for _ in range(m)] for _ in range(n)]


def dfs(row, col):
    global count
    visited[row][col] = True
    if col == m - 1:
        count += 1

    for i in range(3):
        next_x, next_y = row + dx[i], col + dy[i]
        if 0 <= next_x < n and 0 <= next_y < m:
            if graph[next_x][next_y] != "x" and not visited[next_x][next_y]:
                dfs(next_x, next_y)

for i in range(n):
    dfs(i, 0)

print(count)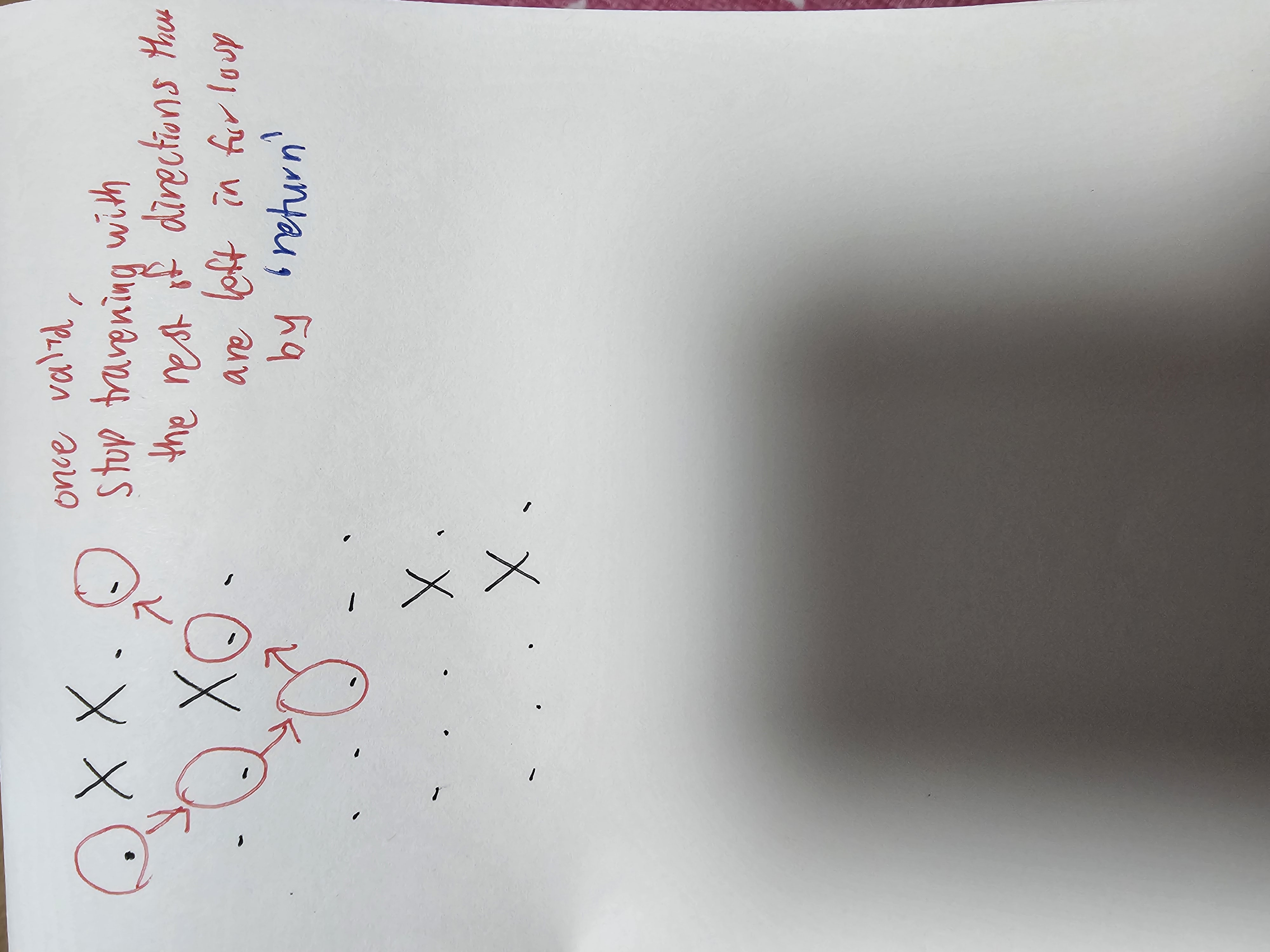

Yes we need to return once we meet the condition or else it will traverse the leftover directions! But just adding return is not all! Because once that dfs call stack ends and we recur one step back at prior positon, we still traverse the leftover directions. So I placed a break after the dfs call like this. But this is wrong!

def dfs(row, col):
    global count
    visited[row][col] = True
    if col == m - 1:
        count += 1
		return

    for i in range(3):
        next_x, next_y = row + dx[i], col + dy[i]
        if 0 <= next_x < n and 0 <= next_y < m:
            if graph[next_x][next_y] != "x" and not visited[next_x][next_y]:
                dfs(next_x, next_y)
                break

Why? While we want to break out of all dfs recursive stack once we meet the right condition, if we dont meet the right condition, we still want to traverse the leftover directions. So we should not place a break because if you have

5 5
.xx.x
..x.x
....x
...x.
...x.

Even if we go 1 step back, dir[1] cannot be traversed cuz of break. So only when we meet the right condition, we return True and that will be a flag where if future dfs returns True, that means a valid path has been formed. We make dfs return a boolean and if it returns True at the end of recursion, we return True and break out of all dfs loops.

revisited jan 13th

so diff between return and break is well explained by past me. But when dfs doesnt return True from the previous call stack, (i.e. invalid path) then i iterates to the next value in the current call stack. But if it is a valid path where dfs returns True, we dont make i iter to next value (dont make it to backtrack and iter other i values). Instead, we return all the way till the start point. Debug and it is easier to see the diff.

i tried adding break instead of return True when if dfs but it is wrong. why?

solution

import sys
input = sys.stdin.readline
from collections import defaultdict, deque

n, m = map(int, input().split())
graph=[list(input().strip()) for _ in range(n)]
count = 0
dy = [1, 1, 1]
dx = [-1, 0, 1]
visited = [[False for _ in range(m)] for _ in range(n)]


def dfs(row, col):
    global count
    visited[row][col] = True
    if col == m - 1:
        count += 1
        return True

    for i in range(3):
        next_x, next_y = row + dx[i], col + dy[i]
        if 0 <= next_x < n and 0 <= next_y < m:
            if graph[next_x][next_y] != "x" and not visited[next_x][next_y]:
                if dfs(next_x, next_y):
                    return True
    return False

for i in range(n):
    dfs(i, 0)

print(count)

better

i think this is impl better

import sys
input = sys.stdin.readline
answer = 0
def dfs(x, y):
    if y == C-1:
        return True
    for dx in [-1,0,1]:
        ax = x + dx
        ay = y + 1
        if 0 <= ax < R and 0 <= ay < C:
            if board[ax][ay] != "x" and visited[ax][ay] == -1:
                visited[ax][ay] = 1
                if dfs(ax, ay):
                    return True
    return False


R, C = map(int,input().split())
visited = [[-1 for _ in range(C)] for _ in range(R)]
board = [list(input().strip()) for _ in range(R)]
for i in range(R):
    if dfs(i, 0): answer += 1
print(answer)

complexity

The time complexity of this code is O(n * m), where n is the number of rows and m is the number of columns in the grid. This is because the code uses a depth-first search (DFS) to explore the grid, and in the worst case, it visits every cell in the grid once.

The space complexity of this code is O(n * m) as well. This is because it uses a 2D list visited to keep track of visited cells, and in the worst case, it needs to store a boolean value for each cell in the grid.

Overall, the code has a time and space complexity of O(n * m) due to the DFS traversal of the grid.