[Leetcode] 104. Maximum Depth of Binary Tree

https://leetcode.com/problems/maximum-depth-of-binary-tree/description/

initial

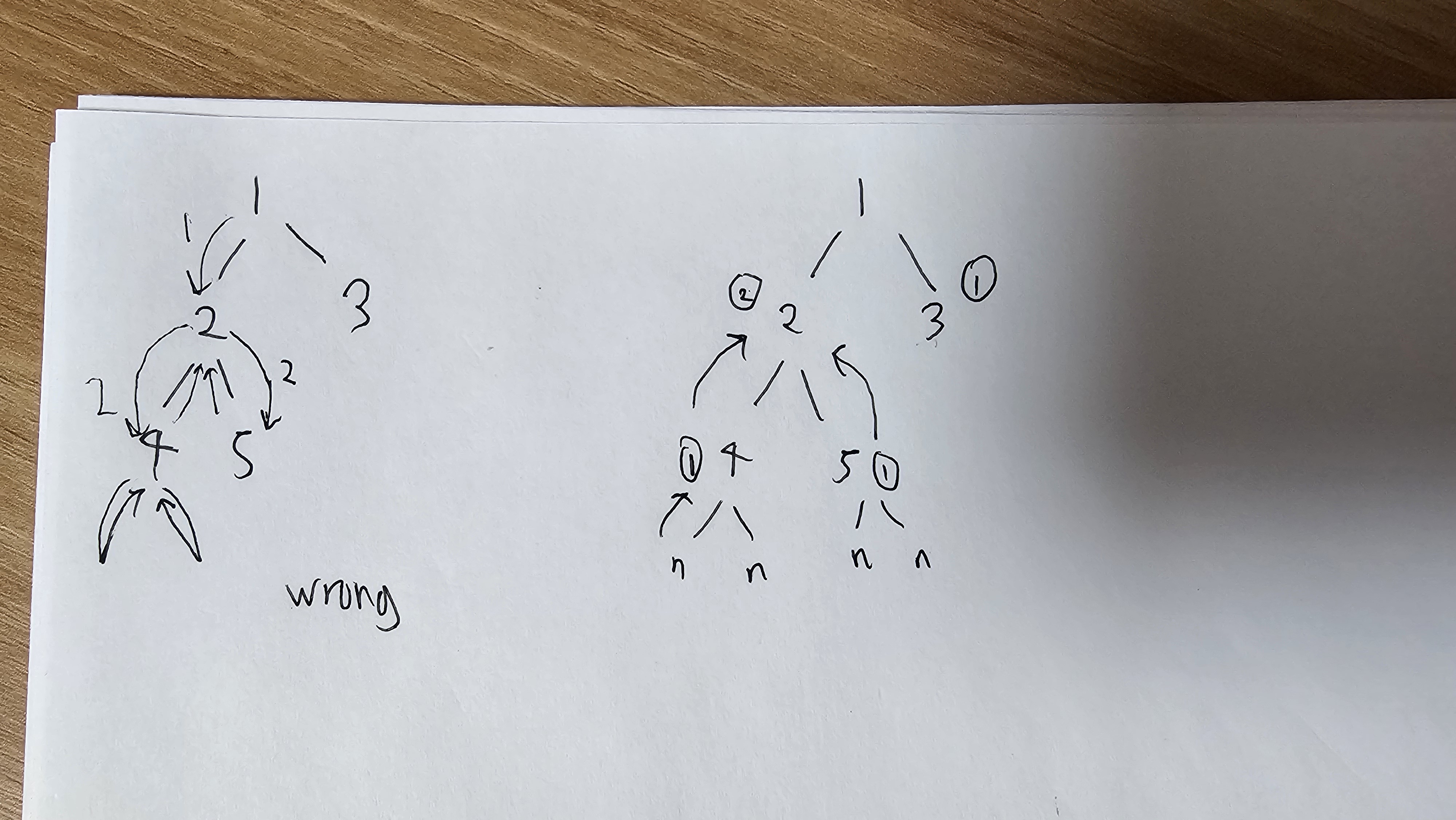
So we can do 2 ways- top-down or bottom-up approach. For top down like on the left, we need to increment the depth as we traverse down and collect that depth value.

Like that 빵집 example, when we encounter a node that is None (i.e. leaf node's left or right node will be None), then we return the depth. This return will traverse all the way through the call stack and the value will be updated.

For bottom-up, when node is None, we return 0. This 0 will be updated back to the parent node, where

max(self.maxDepth(node.left) , self.maxDepth(node.right)) +1
max(0,0)+1

so the parent node will have value 1. And it goes up until root.left node.

top-down

from typing import Optional

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.val = value
        self.left = left
        self.right = right

class Solution:
    def maxDepth(self, root: Optional[TreeNode], val=1) -> int:
        if root is None:
            return val - 1
        left_depth = self.maxDepth(root.left, val + 1)
        right_depth = self.maxDepth(root.right, val + 1)
        return max(left_depth, right_depth)

# Example usage
if __name__ == "__main__":
    # Create a sample binary tree
    #        1
    #       / \
    #      2   3
    #     /
    #    4
    root = TreeNode(1)
    root.left = TreeNode(2, TreeNode(4))
    root.right = TreeNode(3)

    # Create a Solution instance
    solution = Solution()

    # Call the maxDepth method and print the result
    result = solution.maxDepth(root)
    print(result)

bottom-up

from typing import Optional

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.val = value
        self.left = left
        self.right = right

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

# Example usage
if __name__ == "__main__":
    # Create a sample binary tree
    #        1
    #       / \
    #      2   3
    #     /
    #    4
    root = TreeNode(1)
    root.left = TreeNode(2, TreeNode(4))
    root.right = TreeNode(3)

    # Create a Solution instance
    solution = Solution()

    # Call the maxDepth method and print the result
    result = solution.maxDepth(root)
    print(result)

complexity

so time was it n?
and space there is worst case of n and best case of log n?

yes

Let's analyze the time and space complexity of the maxDepth method:

Time Complexity:

The time complexity of the maxDepth method is O(n), where n is the number of nodes in the binary tree.

• Explanation:
  • The method traverses each node in the binary tree exactly once.
  • The recursion goes through all nodes, and the work done at each node is constant.

Space Complexity:

The space complexity is O(h), where h is the height of the binary tree.

• Explanation:
  • The space used by the call stack during recursion is proportional to the height of the tree.
  • In the worst case, where the tree is completely unbalanced (skewed), the height is equal to the number of nodes (O(n)).
  • In the best case, where the tree is perfectly balanced, the height is log₂(n) (assuming a binary tree with n nodes).

In summary, the time complexity is O(n) because each node is visited once, and the space complexity is O(h) due to the call stack during recursion, where h is the height of the tree.