[Leetcode] 110. Balanced Binary Tree

https://leetcode.com/problems/balanced-binary-tree/description/

initial

its similar to finding height of binary tree. I compared that if root.left's subtree and root.right's subtree height difference is less than 2 it is true.

But i missed out a v impt case. What if we have

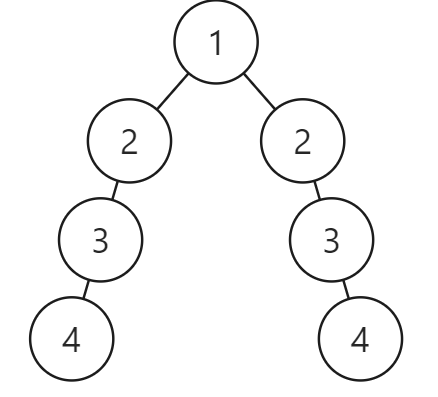
The question defined height balanced as "depth of the two subtrees of every node never differs by more than one". So it is not just root.left and root.right but for a given node like node 2, its left (3-4) and right (none) subtrees height differs by 2, so this is False. So we have to check for each node as well, not just root.left and root.right.

solution

class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        def calc_height(node:Optional[TreeNode]) -> int:
            return max(calc_height(node.left),calc_height(node.right))+1 if node else 0
        if not root:
            return True
        left = calc_height(root.left)
        right= calc_height(root.right)
        return abs(left-right) <2 and self.isBalanced(root.left) and self.isBalanced(root.right)

complexity

time is n^2. it is normally n but since we are checking for EACH NODE, it is n* n.

space as usual is h worst case and log n best case but since it is PERFECTLY BALANCED binar ytree, it is log n