https://school.programmers.co.kr/learn/courses/30/lessons/67259
Initial try
In my queue, the parameters that I store will lead to wrong answer. I store the previous directions as well where we go either right or down from [0,0].
from collections import deque
def solution(board):
visited= [[False for _ in range(len(board[0]))] for _ in range(len(board))]
length = len(board)
queue = deque()
# queue.append((0, 0, 0, dir))
answer=[]
queue.append((0, 0, 1, 0, 0))
queue.append((0,0,0,1,0))
visited[0][0] = True
while queue:
moves = [[1,0],[-1,0],[0,-1],[0,1]]
x,y,prevX,prevY, cost = queue.popleft()
for move in moves:
dx,dy= x+move[0],y+move[1]
if dx<0 or dx>=len(board[0]) or dy<0 or dy>=length or board[dx][dy]==1:
continue
if dx == len(board[0]) - 1 and dy == length - 1:
answer.append(cost)
cost += check_direction(move[0],move[1],prevX,prevY,cost)
print(cost)
if not visited[dx][dy]:
visited[dx][dy]= True
queue.append((dx,dy,move[0],move[1],cost))
print((dx,dy,move[0],move[1],cost))
return min(answer)
def check_direction(nextX,nextY,prevX,prevY,cost):
if prevX == nextX and prevY==nextY:
cost+=100
else:
cost+=500
return cost
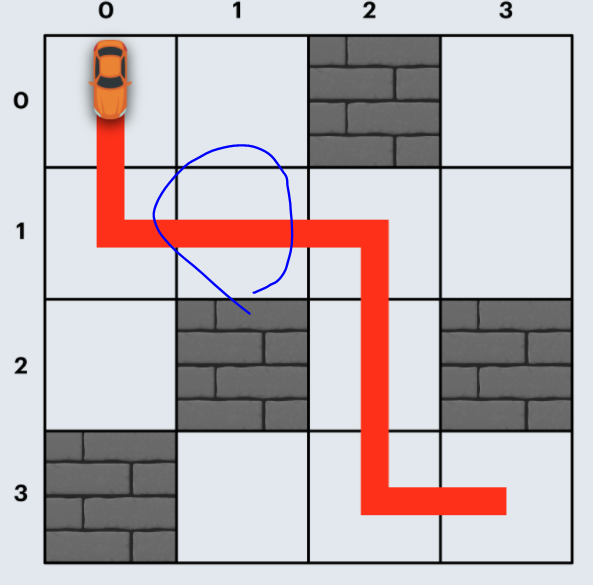
solution([[0,0,0],[0,0,0],[0,0,0]])But this will that when bfs starts on starting point 0,0, we can move both directions - right and down. So in this case, we use a little trick that marks a custom direction just for this edge case. We mark the start direction as integer 5 (or -1).
Model Ans (BFS)
[wrong explanation] But official solution is here. We actually dont create a visited list because other paths stored in queue will not be able to visit the already-visited points by another path that has been processed earlier. So instead, we allow possibility that other paths will go back and forth and back and forth because there is no mark of visited points. But we create a price 2d list that record the smallest price of any path that visits that point.
Ok my explanation above is wrong (June 11th fix) So even though there is no visited list, we have this condition that stop unnecessary paths from being added to our queue. The condition is if the point that we are visiting has a cost that is recorded and is higher than our current cost to visit it, we override that value and visit it. So if our current cost is higher, that means there is a path that has lower cost that has been already added to our queue. So, we don’t visit that point and try other path.
the condition is:
if nc <= price[nx][ny]:
price[nx][ny] = nc
queue.append((nx, ny, nc, i))Model ans:
price[-1][-1] will keep being updated with a smaller distance cost as other bfs search paths finish being processed.
from collections import deque
dx = [0, 0, 1, -1]
dy = [1, -1, 0, 0]
def bfs(board):
n = len(board)
price = [[int(1e9)] * n for _ in range(n)]
price[0][0] = 0
queue = deque()
queue.append((0, 0, 0, 5)) # (시작X, 시작Y, 시작Cost, 시작방향)
while queue:
x, y, c, z = queue.popleft()
if x == n - 1 and y == n - 1:
continue
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
nz = i
if nx < 0 or nx >= n or ny < 0 or ny >= n:
continue
if board[nx][ny] == 1:
continue
if z==5:
nc = c + 100
elif nz == z:
nc = c + 100
else:
nc = c + 600
if nc <= price[nx][ny]:
price[nx][ny] = nc
queue.append((nx, ny, nc, i))
return price[-1][-1]
def solution(board):
n = len(board)
answer = bfs(board)
return answerDijkstra Approach
Now looking back [Sep 2nd], we can solve via Dijkstra but I made a big mistake
Fundamental mistake in not resetting cur_cost to 0
My original code:
while heap:
cur_cost, cur_x, cur_y, cur_dir = heapq.heappop(heap)
if cur_x==rows and cur_y==cur_y:
return cur_cost
for i in range(len(moves)):
move=moves[i]
next_x,next_y = cur_x+move[0],cur_y+move[1]
next_dir=0
if next_x<0 or next_x>=rows or next_y<0 or next_y>=cols or board[next_x][next_y]==1:
continue
if i==cur_dir:
cur_cost+=100
next_dir=i
elif cur_dir==5:
cur_cost+=100
next_dir=5
else:
cur_cost+=500
next_dir=i
distance[next_x][next_y]=cur_cost
heapq.heappush(heap, (cur_cost,next_x,next_y,next_dir))When you first iterate at start_point, i=0 and cur_cost=0 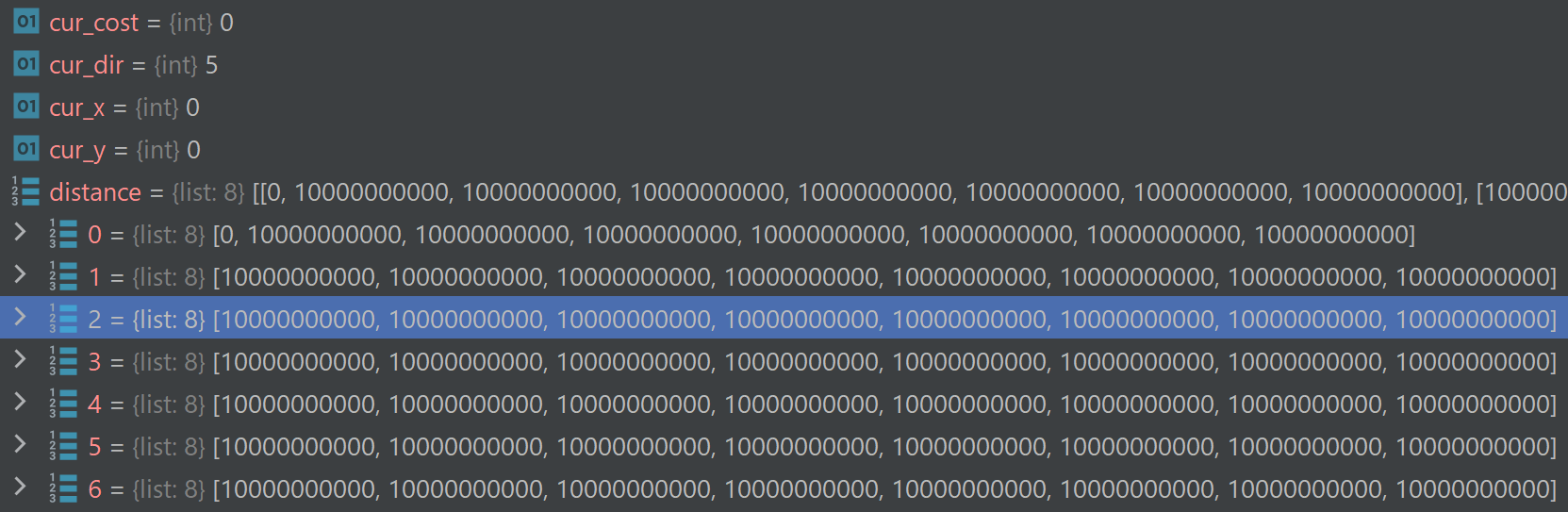
Now when i=0 and when we reach this line, cur_cost would have been updated to 100.
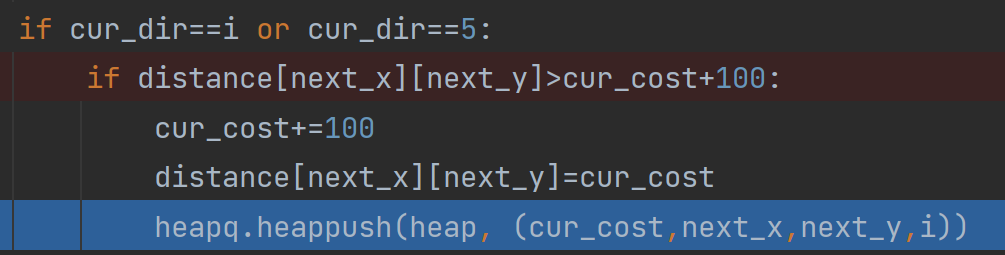
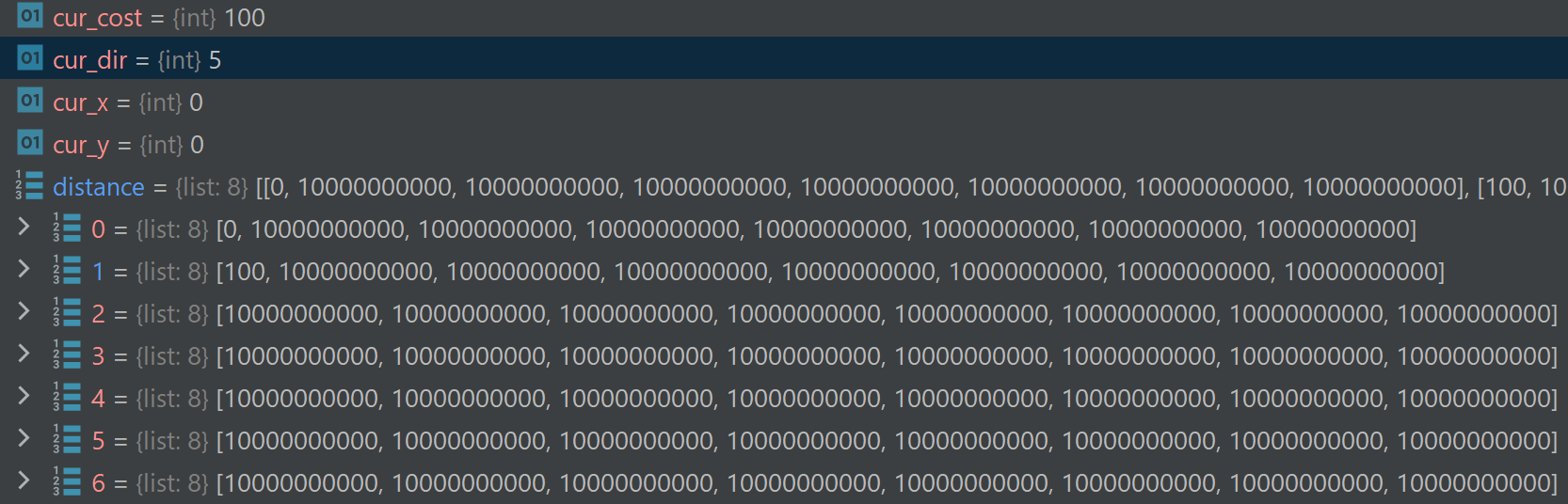
Ok then lets go to i=1. next_x and next_y for i=1 goes out of bounds and we continue to i=2.
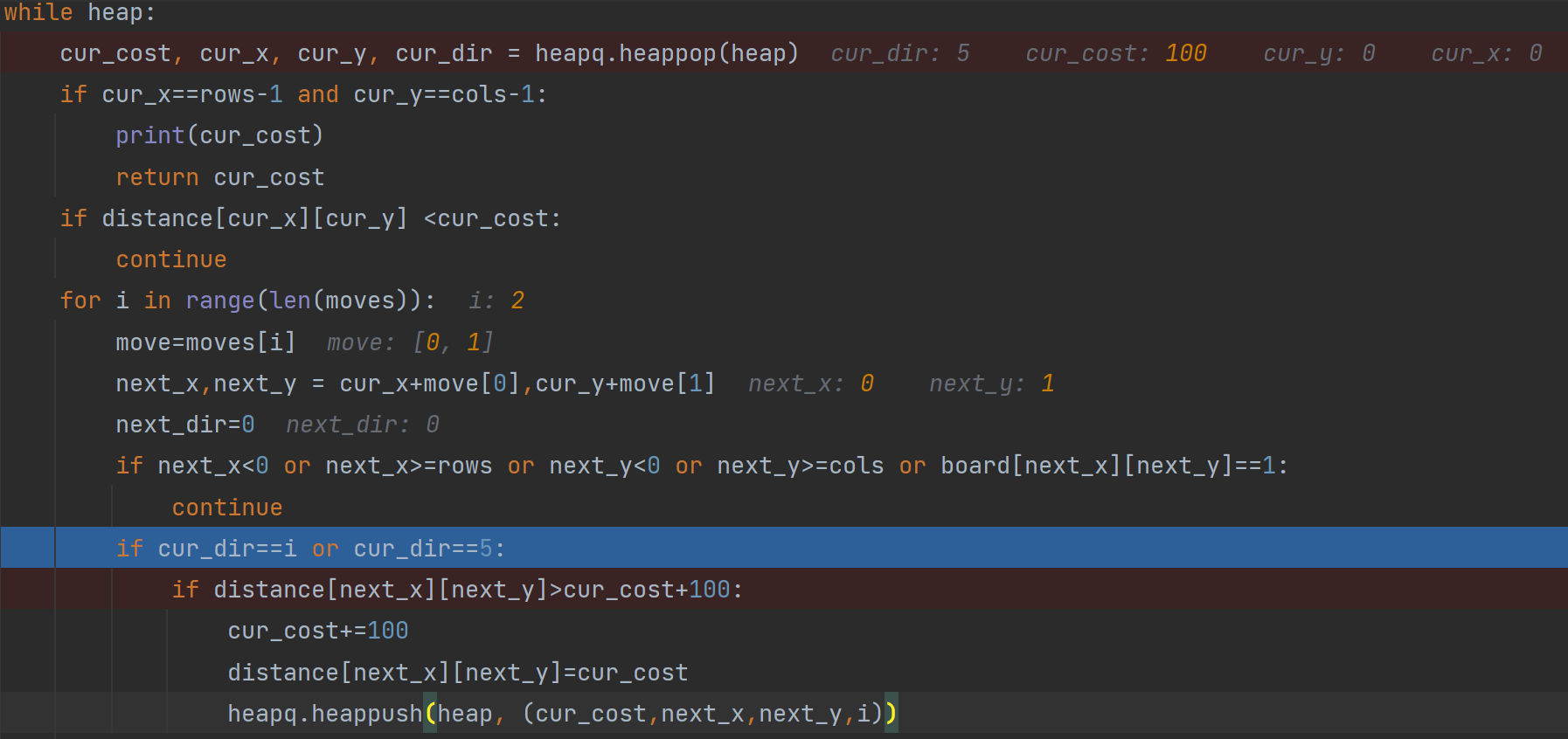
Notice that on the very top of the screenshot, the while heap loop has not reset cur_cost to 0 and the cur_cost value is accumulating as this while heap loop continues on and on.
So when i=2, cur_cost is incremented by 100 and is thus 200. So distance[next_x][next_y] is updated to 200 as such below:
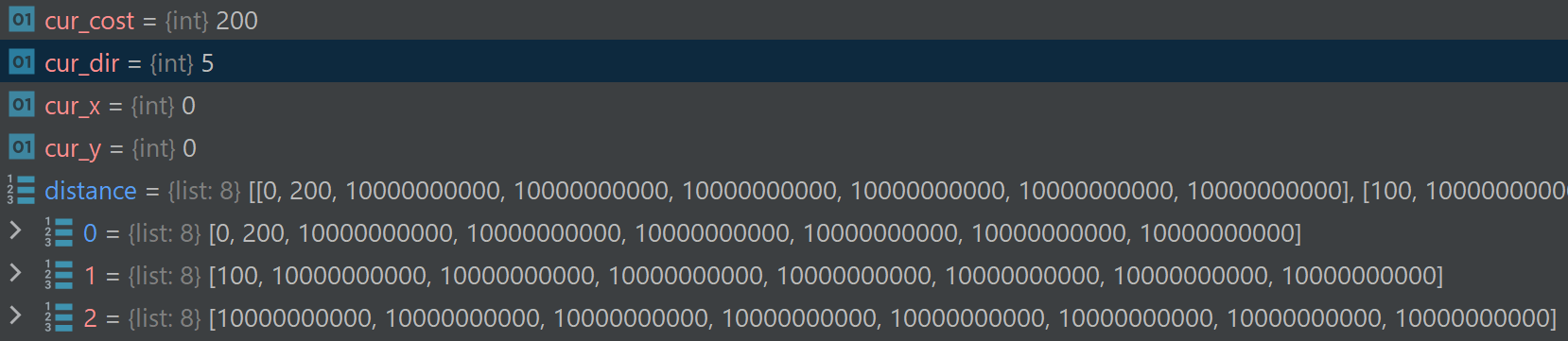
Solution: set new variable for each inner loop
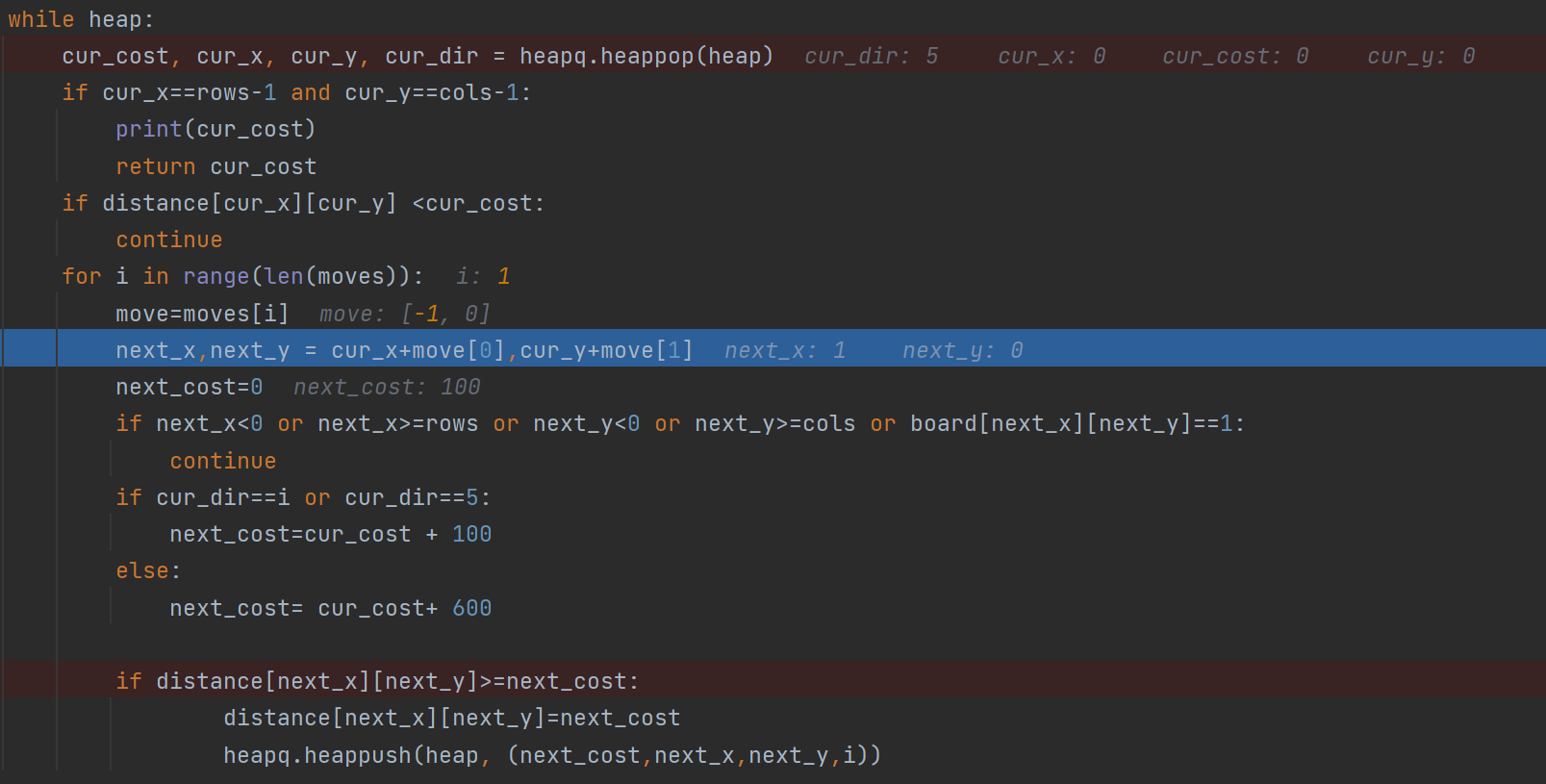
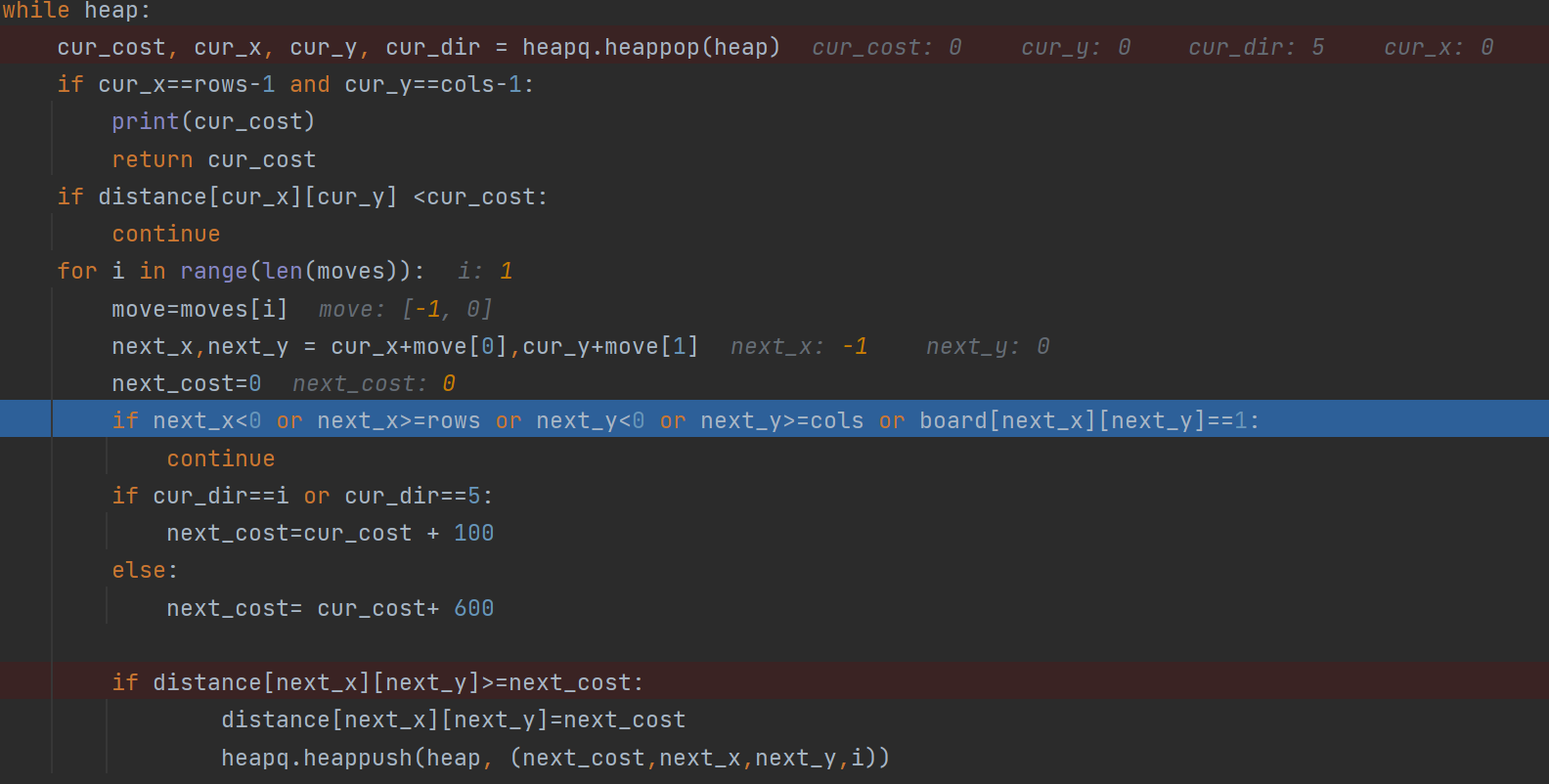
You need to set a new_cost in the inner for loop so that it resets every time this move for loop is conducted.
So after i=0 loop, new_cost is reset from 100 to 0 like this. (Observe the debugging line before and after)
import heapq
def solution(board):
rows = len(board)
cols= len(board[0])
distance = [[int(10e9) for _ in range(cols)] for _ in range(rows)]
distance[0][0]=0
heap = []
heapq.heapify(heap)
heapq.heappush(heap, (0,0,0,5))
moves=[[1,0],[-1,0],[0,1],[0,-1]]
while heap:
cur_cost, cur_x, cur_y, cur_dir = heapq.heappop(heap)
if cur_x==rows-1 and cur_y==cols-1:
print(cur_cost)
return cur_cost
if distance[cur_x][cur_y] <cur_cost:
continue
for i in range(len(moves)):
move=moves[i]
next_x,next_y = cur_x+move[0],cur_y+move[1]
next_cost=0
if next_x<0 or next_x>=rows or next_y<0 or next_y>=cols or board[next_x][next_y]==1:
continue
if cur_dir==i or cur_dir==5:
next_cost=cur_cost + 100
else:
next_cost= cur_cost+ 600
if distance[next_x][next_y]>=next_cost:
distance[next_x][next_y]=next_cost
heapq.heappush(heap, (next_cost,next_x,next_y,i))Or you can do like this below where you don't set new_cost to 0 each time this for loop runs but you create a new_cost variable each time with a calculated value of cur_cost + 100 or 600.
while heap:
cur_cost, cur_x, cur_y, cur_dir = heapq.heappop(heap)
for i in range(4):
next_x = cur_x + moves[i][0]
next_y = cur_y + moves[i][1]
if next_x < 0 or next_y < 0 or next_x >= row or next_y >= col or board[next_x][next_y] == 1:
continue
if cur_dir == 5:
new_cost = cur_cost + 100
elif cur_dir == i:
new_cost = cur_cost + 100
else:
new_cost = cur_cost + 600
if new_cost <= distance[i][next_x][next_y]:
distance[i][next_x][next_y] = new_cost
heapq.heappush(heap, [new_cost, next_x, next_y, i])But using Dijkstra, you need 3d distance list
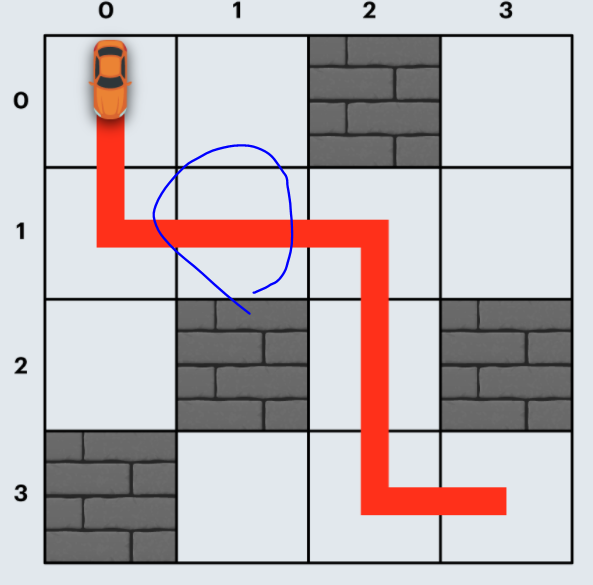
Now this question is very hard to get full marks because besides dijkstra, we need to see another logic in here. Normally in dijkstra, we can just have a 2d cost list and get the cost by x and y. But here there is an exception that requires a 3d cost list which inputs the direction as well.
Notice at (1,1), we can come from either (0,1) or (1,0) and either way the cost is 700. But!! When we go to (1,2) the cost differs. If we come from (1,0) the cost will be 700 + 100 = 800. But If we come from (0,1) the cost is 700 + 600 = 1300. So if (0,1) pathway is processed first and (1,2) is the final end grid, that 1300 will be returned as the wrong answer.
So if we have this kind of cases at distance[-1][-1] where the previous distance is not considered, then it is wrong from some cases. We didnt have this issue with BFS because the cost at end grid is kept being updated and we take the least cost value. In dijkstra, depending on which direction you arrive at a particular grid, the cost may differ. So we need to have a 3d cost list and for the answer, compare all the 4 directions that we may reach board[-1][-1] with.
If you want to be more concise, you can just consider the west and south directions for the end position because other positions are impossible.
distance = [[[int(10e9) for _ in range(col)] for _ in range(row)] for _ in range(4)]The first index will store the direction.
Before I forget v important
if distance[cur_dir][cur_x][cur_y] < cur_cost:
continueWill cause list index out of range error bcos for starting direction I have set as 5 but when I initialised this 3d distance cost list, it is from 0~3 (4 directions). So remove that line above as well. (But then how do we make it more efficient?)
So final model ans:
import heapq
def solution(board):
rows = len(board)
cols= len(board[0])
distance = [[[int(10e9) for _ in range(cols)] for _ in range(rows)] for _ in range(4)]
for i in range(4):
distance[i][0][0]=0
heap = []
heapq.heapify(heap)
heapq.heappush(heap, (0,0,0,5))
moves=[[1,0],[-1,0],[0,1],[0,-1]]
while heap:
cur_cost, cur_x, cur_y, cur_dir = heapq.heappop(heap)
# if cur_x==rows-1 and cur_y==cols-1:
# print(cur_cost)
# return cur_cost
# list index out of range error
# if distance[cur_x][cur_y] <cur_cost:
# continue
for i in range(len(moves)):
move=moves[i]
next_x,next_y = cur_x+move[0],cur_y+move[1]
next_cost=0
if next_x<0 or next_x>=rows or next_y<0 or next_y>=cols or board[next_x][next_y]==1:
continue
if cur_dir==i or cur_dir==5:
next_cost=cur_cost + 100
else:
next_cost= cur_cost+ 600
if distance[i][next_x][next_y]>=next_cost:
distance[i][next_x][next_y]=next_cost
heapq.heappush(heap, (next_cost,next_x,next_y,i))
print(min(distance[0][-1][-1], distance[1][-1][-1], distance[2][-1][-1], distance[3][-1][-1]))
return min(distance[0][-1][-1], distance[1][-1][-1], distance[2][-1][-1], distance[3][-1][-1])Time and space complexity
Time Complexity:
- The code utilizes Dijkstra's algorithm with a priority queue.
- In the worst case, all cells in the grid are processed.
- For each cell, there are up to four possible moves (up, down, left, right).
- The
heapq.heappopandheapq.heappushoperations take O(log(N)) time, where N is the number of cells in the priority queue. - Therefore, the overall time complexity is O(N^2 * log(N)), where N is the number of rows or columns in the grid.
Space Complexity:
- The code uses several data structures that consume memory:
distanceis a 3D array of size 4 x N x N, where 4 represents the four possible directions (up, down, left, right), and N is the number of rows or columns in the grid.- The
heapdata structure stores cell information and can potentially have up to N^2 cells in the worst case.
- Therefore, the overall space complexity is O(4 * N^2) = O(N^2).
In summary, the time complexity is O(N^2 * log(N)), and the space complexity is O(N^2).