[Programmers] 기지국 설치

https://school.programmers.co.kr/learn/courses/30/lessons/12979

Initial approach

I find myself at implementing code, especially greedy questions.

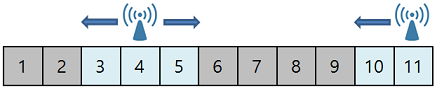
But let's think. Before we know how many stations to fit on the left of the already-built station, the transmission range of a given station is 2w+1.

Then we need to calculate how many stations to put in a range from start pointer to end pointer. For example, it could be from i=1 to i=2 for the first iteration of stations list (because from i=3 to i=5 it is covered by the already built station). Notice the range is end-start+1 and it is +1 because it is inclusive of both start and end positions in this range gap.

2-1 =1 (x)
2-1+1 = 2 (o)

If this range length is less than 0, there is no need for towers to be built so continue.

Then we just divide the range over the transmission range(2w+1) and round it up with math.ceil() to find how many stations to put in that given range from start to end pointer. Finally, update start pointer to the right of the tower (start = station+w+1)

This loop will work right until the final station's left side. But if there are remaining apartments on the right side after the loop that are not covered,

If n (the total number of apartments) is greater than or equal to the start position, it means there are uncovered apartments on the right side.
Calculate the left_over apartments by subtracting start from n and adding 1. Again, the +1 accounts for the last apartment.
Calculate the number of additional base stations required to cover the remaining apartments by dividing left_over by (2*w + 1) and taking the ceiling value. Add this value to the answer.

my wrong code:

import math

def solution(n, stations, w):
    answer = 0
    start,end=1,1
    for station in stations:

        end=station-w-1
        length=end-start+1
        if 2*w+1>=length:
            answer+=1
        else:
            answer += math.ceil(length/(2*w+1))
        start = station+w+1
    if start<n:
        left_over = n-start+1
        answer += math.ceil(left_over/(2*w+1))
    print(answer)
    return answer

Solution

import math

def solution(n, stations, w):
    answer = 0
    start,end=1,1
    for station in stations:
        end=station-w-1
        length=end-start+1
        if length>0:
            answer += math.ceil(length/(2*w+1))
        start = station+w+1
    if n>=start:
        left_over = n-start+1
        answer += math.ceil(left_over/(2*w+1))
    print(answer)
    return answer

Complexity

The time complexity of this solution is O(N), where N is the total number of apartments. The function iterates through the stations array once and calculates the number of additional base stations needed based on the positions of existing stations and gaps between them. The calculation is performed in a linear pass through the array, so it is directly proportional to the number of apartments.

The space complexity is O(1) because the solution uses a constant amount of additional space to store variables (answer, start, end, length, and left_over) that do not depend on the input size. The size of the stations array or the number of apartments does not affect the space complexity of the algorithm.