[Programmers] 부대복귀

https://school.programmers.co.kr/learn/courses/30/lessons/132266

Initial approach (Runtime)

This is a typical BFS question but if you think it is that simple, wait till you get this Runtime error in your face. If you do BFS for each source to calculate distance from source to destination, you will get runtime issues.

Initial idea

What you should do instead is try and find a way to do just 1 BFS search. My first thought was that to complete just 1 BFS search and get all the distances we need, what if we start from destination instead? Then what would be the end condition to break out of recursive loop?

Initially, I thought this way

while queue:
	cur_city, cur_cost = queue.popleft()
	for source in sources:
    	if cur_city==source:
        	ans.append(cur_cost)
	

That will work if cost does need to be matched with the city in the answer list but appending will disregard the order. If a city with least cost is encountered first but if that city's number is big like 9, then since the order is disregarded, the answer will be wrong.

[Revising in Sep 6th 23] Then what if we store the cost and the city in a dictionary? Then as we iterate through the source, if there is a value stored for that key(source) we return that value and if not we return -1. Will that work?

from collections import deque, defaultdict
def solution(n, roads, sources, destination):
    ans = []
    queue = deque()
    graph = defaultdict(list)
    dic={}
    for road in roads:
        start,end=road
        graph[start].append(end)
        graph[end].append(start)
    queue.append((destination,0))
    visited = [False for _ in range(n+1)]
    visited[destination]= True
    
    def bfs(graph,queue,n):
        while queue:
            cur_city, cur_cost = queue.popleft()
            for source in sources:
                if cur_city==source:
                    dic[cur_city] = cur_cost
            for city in graph[cur_city]:
                if not visited[city]:
                    queue.append((city,cur_cost+1))
                    visited[city]=True
                    
    bfs(graph,queue,n)
    ans = []
    for source in sources:
        if source in dic:
            ans.append(dic[source])
        else:
            ans.append(-1)
    return ans

Yes it works!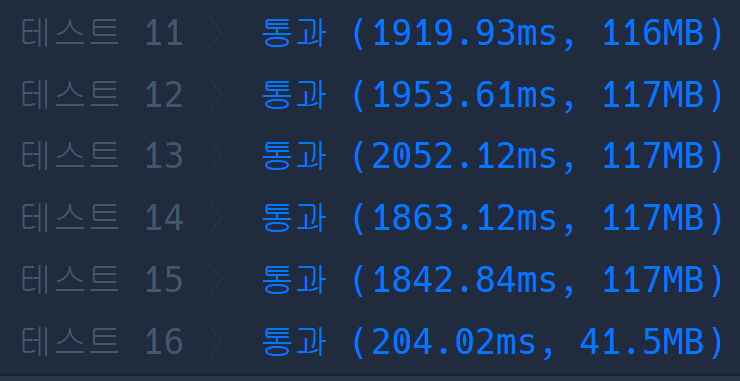

Solution (more time efficient)

Let's look at other way. But first there is a fundamental question. is it necessary to check if current city is indeed one of the sources? If we can just get the ordered cost that matches with the city's number, then this check is unnecessary.

Then, how about using a distance list that is of size (n+1) not n cus it will cause list index out of range error and just adding 1 to cur_cost and appending that cost to that particular index's cost? Then we are getting an ordered way of updating any city's cost from destination as BFS is carried out.

Not only that, it works as a visited list too. If value is -1 for that city, it means it is not visited yet so we can visit it. But if it has a value that is not 1, it has been visited and we continue our traversal from there.

    while queue:
        cur_city, cur_cost = queue.popleft()
        for city in graph[cur_city]:
            if distance[city]==-1:
                queue.append((city,cur_cost+1))
                distance[city]=cur_cost+1
    return distance

correct solution

from collections import deque, defaultdict
def solution(n, roads, sources, destination):
    ans = []
    queue = deque()
    graph = defaultdict(list)
    for road in roads:
        start,end=road
        graph[start].append(end)
        graph[end].append(start)
    queue.append((destination,0))
    distance = [-1] * (n+1)
    distance[destination]=0
    distance = bfs(graph,queue,distance,n)
    return list(distance[source] for source in sources)

def bfs(graph,queue,distance,n):
    while queue:
        cur_city, cur_cost = queue.popleft()
        for city in graph[cur_city]:
            if distance[city]==-1:
                queue.append((city,cur_cost+1))
                distance[city]=cur_cost+1
    return distance

Complexity

Model ans

The time and space complexity of your solution function depends on the underlying breadth-first search (BFS) algorithm you're using. Let's analyze the complexity:

Time Complexity:

• Building the graph from the roads list takes O(E) time, where E is the number of edges in the graph (size of roads).
• Initializing distance with -1 for each node takes O(N) time, where N is the number of nodes (cities).
• The BFS traversal itself takes O(V + E) time, where V is the number of vertices (cities) and E is the number of edges.
• The final step of returning the result list also takes O(K), where K is the number of sources.

So, the overall time complexity is O(E + N + V + E + K), which simplifies to O(N + E + V + K).

Space Complexity:

• The graph dictionary uses O(E) space for storing the edges.
• The queue can take up to O(V) space in the worst case.
• The distance list uses O(N) space.
• The ans list uses O(K) space to store the results.

So, the overall space complexity is O(N + E + V + K).

Keep in mind that the exact values of N, E, V, and K depend on the input data, so the complexity may vary in practice. However, the analysis above provides a general understanding of how the time and space complexity scales with respect to the input sizes and the number of sources.

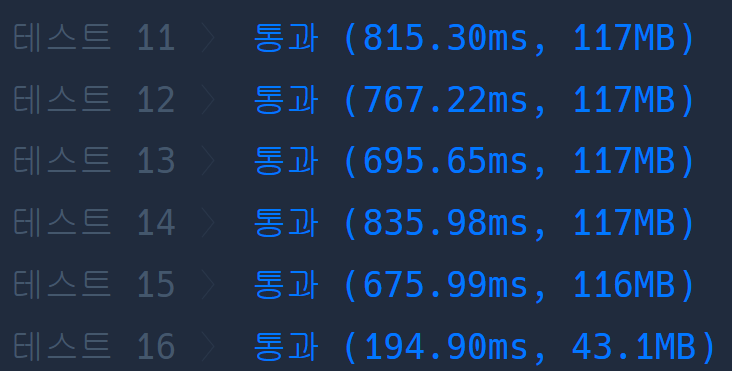
Looks like this is more efficient.

my dictionary solution

What about my dictionary solution?

Time Complexity:

• Building the graph from the roads list takes O(E) time, where E is the number of edges in the graph (size of roads).
• Initializing the visited list with False for each node takes O(N) time, where N is the number of nodes (cities).
• The BFS traversal itself takes O(V + E) time, where V is the number of vertices (cities) and E is the number of edges. Within the BFS, you iterate through the sources list in each step, which can take up to O(K) time for each vertex visited (K is the number of sources).
• The final step of constructing the ans list takes O(K) time.

So, the overall time complexity is O(E + N + (V + E) * K), which simplifies to O(N + E + VK).

Space Complexity:

• The graph dictionary uses O(E) space for storing the edges.
• The queue can take up to O(V) space in the worst case.
• The visited list uses O(N) space.
• The dic dictionary is used to store the distance to each source city, which can take up to O(K) space.
• The ans list uses O(K) space to store the results.

So, the overall space complexity is O(N + E + V + K).

Your code should work correctly and efficiently to find the shortest distances from the destination city to the specified sources cities.