Segment Tree (+template)

https://leetcode.com/problems/fruits-into-baskets-iii/description/?envType=daily-question&envId=2025-08-06

segment tree

A segment tree is a data structure used to efficiently handle range queries and point updates on an array. Its basically a binary tree in the form of a long list (4n) size where root node is at index 0, and for a given node i, its left child is is stored not at i-1 but at 2i+1 and right child is at 2i+2. That is why we made it 4n in the first place to store these nodes in a list.

The Analogy 🧮
Imagine you have a long list of numbers, like daily sales data for a month.

A normal array would be like a single list. If you want the total sales for the first two weeks, you have to manually add up all 14 numbers. If you update a single day's sale, that's easy. But if you want a different two-week period, you have to add a new set of numbers.

A segment tree is like a neatly organized set of folders and sub-folders. The main folder holds the total sales for the entire month. Inside are two sub-folders, one for the first half of the month and one for the second half. Each of those folders contains the total sales for its period. This continues until you have a folder for each individual day.

To find the total sales for a specific range (e.g., from day 5 to day 10), you don't have to add up each individual day. You simply look at the folders that cover that range. You might grab the folder for days 5-8 and the folder for days 9-10 and add their pre-calculated totals together. This is much faster than summing up each individual day.

structure

So

How it Works

The tree is built from the bottom up. When we reach leaf node, we update its value with the absolute value given in the original list. But parents of these leaf nodes - will be the sum of the leaf nodes, or max of them or min of them (depends on the q). We also need to update the leaf node and up if that specific value is changed.

fruits = [4,2,5], baskets = [3,5,4]
for example, the root node will store the max of left and right child nodes.

Root Node (Range [0, 2]): max(5, 4) = 5.

Left Child (Range [0, 1]): max(3, 5) = 5.

Right Child (Range [2, 2]): The leaf node value is 4.

Left Grandchildren: Leaf nodes with values 3 and 5.

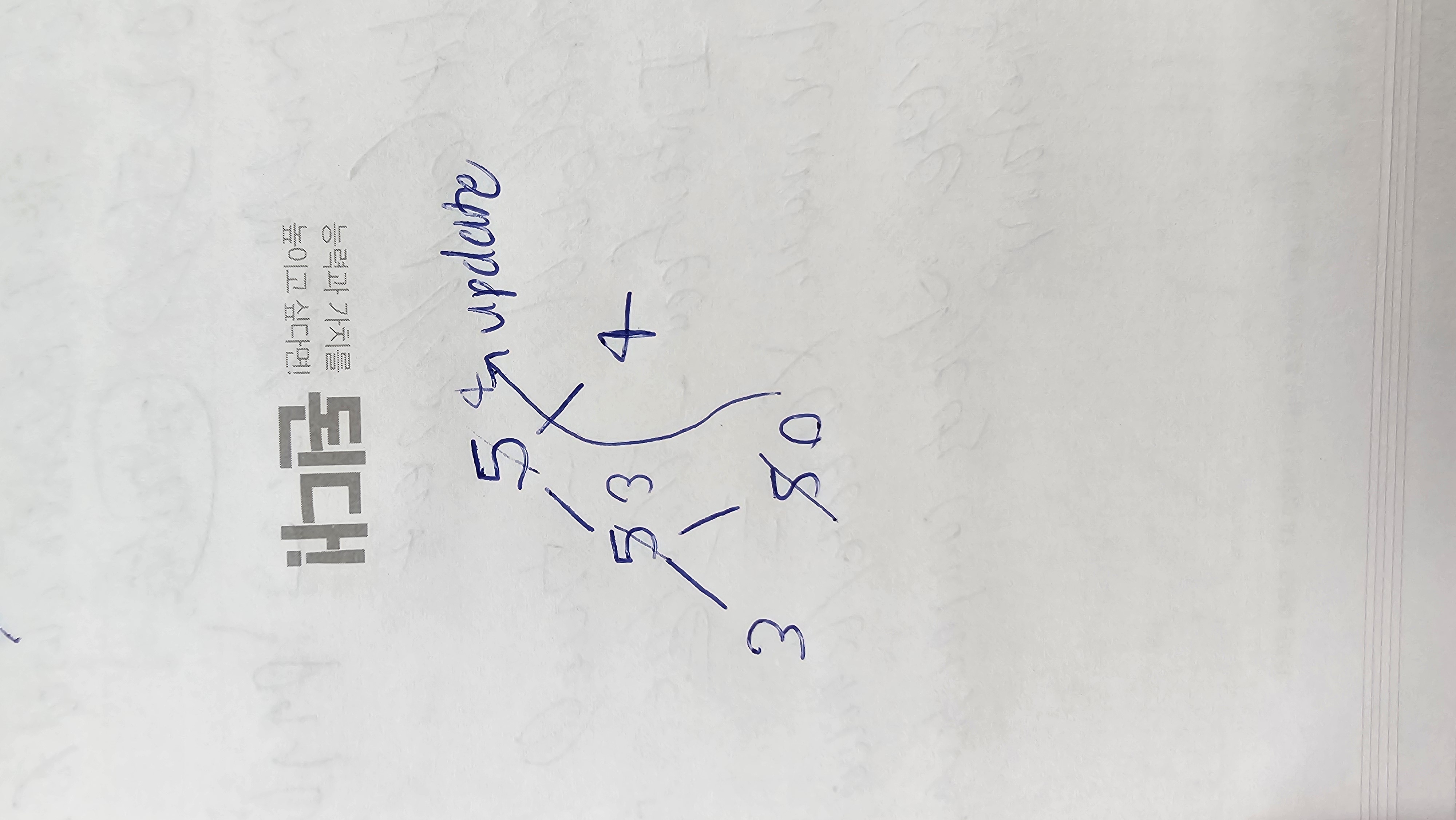
When fruit 4 comes, We need to find the leftmost basket with capacity >= 4.

The query starts at the root (max capacity 5).

We check the left child (max capacity 5). Since 5 >= 4, we go left.

We check the left grandchild (capacity 3). Since 3 < 4, this basket is too small. We go right.

We check the right grandchild (capacity 5). Since 5 >= 4, this is a valid basket. We have found the leftmost basket, which is baskets[1].

Update: We place the fruit in baskets[1]. The capacity of this basket becomes 0.

The segment tree is updated to reflect this change. The value of the node for baskets[1] becomes 0. Its parent (range [0, 1]) is updated to max(3, 0) = 3. The root node is updated to max(3, 4) = 4.

confusing part

        # base case
        if start==end:
            self.tree[node]=0
            return start

this is only valid for leaf nodes so if both nodes are value 0, the parent node will be 0.And the grandparent's traversal will go to the other paret node if theres a value that matches the quantity.

solution

class SegmentTree:
    def __init__(self,arr):
        self.n=len(arr)
        self.tree=[0]*(4*self.n)
        self.arr=arr
        self._build(0,0,self.n-1)

    def _build(self,node,start,end):
        if start==end:
            self.tree[node]=self.arr[start]
            return

        mid = (start+end)//2
        self._build(2*node+1,start,mid)
        self._build(2*node+2,mid+1,end)

        self.tree[node]= max(self.tree[2*node+1], self.tree[2*node+2])

    def _update_point(self,node,start,end,fruit_quantity):
        # base case
        if start==end:
            self.tree[node]=0
            return start
        mid=(start+end)//2
        if self.tree[2*node+1]>=fruit_quantity:
            idx = self._update_point(2*node+1,start,mid,fruit_quantity)
        elif self.tree[2*node+2]>=fruit_quantity:
            idx = self._update_point(2*node+2, mid+1,end, fruit_quantity)
        else:        
            return -1
        
        self.tree[node]=max(self.tree[2*node+1],self.tree[2*node+2])
        return idx
    
    def find_and_update(self,quantity):
        if self.tree[0]<quantity:
            return -1
        return self._update_point(0,0,self.n-1,quantity)

class Solution:
    def numOfUnplacedFruits(self, fruits: List[int], baskets: List[int]) -> int:
        tree= SegmentTree(baskets)
        ans=0
        for fruit in fruits:
            if tree.find_and_update(fruit)==-1:
                ans+=1
        return ans
        

complexity

A segment tree has a time complexity of $O(\log n)$ for both query and update operations, and a space complexity of $O(n)$ for storing the tree itself.

---

Time Complexity

• Build Operation: Building the segment tree initially takes $O(n)$ time because each of the n leaf nodes and approximately n-1 internal nodes is visited exactly once.
• Query Operation: A range query takes $O(\log n)$ time. This is because at each level of the tree, the algorithm only needs to explore at most two branches (the left and right children). The height of the tree is $O(\log n)$, so the total time complexity is proportional to the tree's height.
• Update Operation: A point update also takes $O(\log n)$ time. The algorithm traverses a single path from the root to a leaf node and then updates the values on the way back up to the root. Since the path length is the height of the tree, the time complexity is $O(\log n)$.

---

Space Complexity

• The space complexity is $O(n)$. A segment tree requires a storage array of size up to $4n$ in the worst case to accommodate all the nodes. For an array of size n, the tree will have n leaf nodes and up to n-1 internal nodes. A safe upper bound for the total number of nodes is $2n - 1$, but using an array of size $4n$ is a common practice to avoid complex power-of-2 calculations and simplifies implementation.